
이번에는 Dynamic Programming 이 적용될 수 있음을 나타내는 두 가지 특성을 살펴보자.
첫번째, Overlapping Subproblems. 해결하고자 하는 복잡한 문제가 여러가지의 하위 문제들로 나뉠 수 있다는 의미이다. Divide and Conquer 과 같지만, Dynamic Programming은 그저 나누어 해결하는 것만이 목적이 아니라 나누어 해결한 문제의 결과를 저장하고, 이후 동일한 중복되는 문제가 존재할 때 새로 컴퓨팅을 하는 것이 아니라 결과값만을 가져와 문제해결의 효율을 높일 수 있다는 특징을 가진다. 따라서, Dynamic Programming은 중복되는 subproblems로 나뉠 수 있는 복잡한 문제를 해결할 때 사용할 수 있을 것이다.
두번째, Optimal Substructure. 잘 이해되지 않았기에 찾아본 결과, Main Problem의 최적해(optimal solution)는 Sub Problem의 최적해들의 집합으로 이루어진다는 것이다.
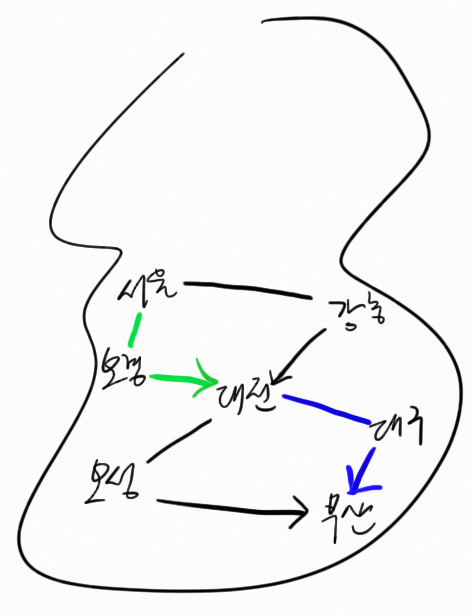
예를 들어 서울에서 부산을 가는 것이 Main problem이라 하자. 꼭 중간에 대전을 들러야 한다고 할 때, 문제는 (1) 서울부터 대전을 가는 일 과 (2) 대전에서 부산을 가는 일 두 가지로 나누어 질 수 있다. 이 때, Main problem의 최적해는 (1)과 (2) 각각의 최적해의 합과 같을 것이다. 위키피디아에는 다음과 같이 서술되어 있다.
In computer science, a problem is said to have optimal substructure if an optimal solution can be constructed from optimal solutions of its subproblems. This property is used to determine the usefulness of dynamic programming and greedy algorithms for a problem.
아하하!
그런데, 작은 문제들의 최적해의 합이 큰 문제의 최적해의 합과 동일하다는 말은 언뜻 당연하게 들릴 수 있다. 그렇다면, Optimal substructure가 적용되지 않는 반례에는 무엇이 있을까?
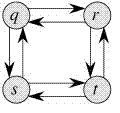
위 그림에서 q에서 t로 가는 최장거리를 구하는 문제 를 해결하려고 한다.
중복된 노드를 지나는 것을 허락하지 않을 때, 최적해는 q->r->t 로 가는 방법과 q->s->t로 가는 방법 두 가지가 있다.
그러나 q->r->t 의 Sub problems 인 q->r 의 최대경로는 q->s->t->r 이고, r->t 최대경로는 r->q->s->t 이다. 따라서 Main problem의 최적해와 Sub problem들의 최적해의 집합이 서로 다른 것을 알 수 있다. q->s->t 의 경우도 마찬가지다.
결과적으로 DP가 적용되려면
- 큰 문제들을 작은 문제들로 나눌 수 있어야 하고,
- (Divide and Conquer와 다르게) 해당 작은 문제들 사이에 중복되는 문제가 존재하여 효율성을 개선할 수 있는 여지가 있어야 하고,
- 작은 문제들의 최적해의 집합이 큰 문제의 최적해와 일치해야 한다. (Optimal substructure)
고 정리할 수 있겠다.
다음 포스팅에서는 DP를 활용하여 어떻게 문제를 해결할 수 있는지 알아보자.
