[알고리즘 풀이 분석] BOJ 1600 말이 되고픈 원숭이

어제 하루 쉬고 오늘 풀어본 문제는 BOJ 1600 말이 되고픈 원숭이 이다! 이번주에 풀어오던 문제들과 동일한 골드IV 문제이고, 몇일전에 풀었던 BOJ 2206 벽 부수고 이동하기 문제와 상당히 유사하다!

BOJ 1600 말이 되고픈 원숭이

동물원에서 막 탈출한 원숭이 한 마리가 세상구경을 하고 있다. 그 녀석은 말(Horse)이 되기를 간절히 원했다. 그래서 그는 말의 움직임을 유심히 살펴보고 그대로 따라 하기로 하였다. 말은 말이다. 말은 격자판에서 체스의 나이트와 같은 이동방식을 가진다. 다음 그림에 말의 이동방법이 나타나있다. x표시한 곳으로 말이 갈 수 있다는 뜻이다. 참고로 말은 장애물을 뛰어넘을 수 있다.

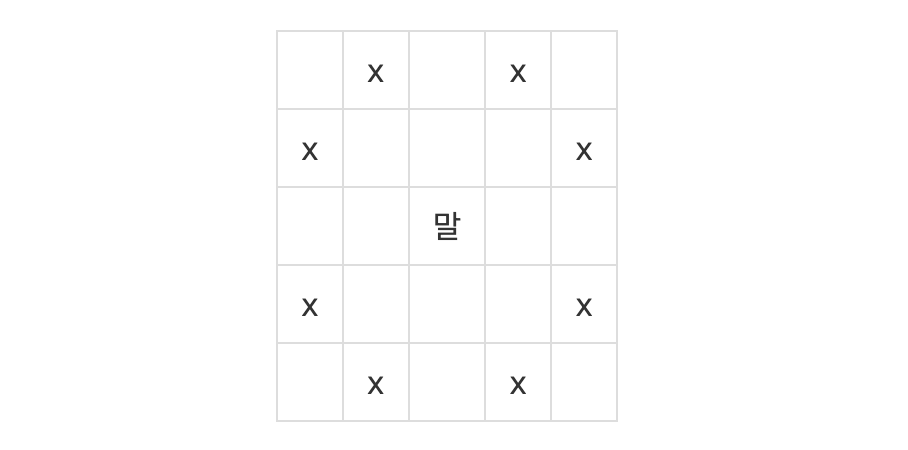
근데 원숭이는 한 가지 착각하고 있는 것이 있다. 말은 저렇게 움직일 수 있지만 원숭이는 능력이 부족해서 총 K번만 위와 같이 움직일 수 있고, 그 외에는 그냥 인접한 칸으로만 움직일 수 있다. 대각선 방향은 인접한 칸에 포함되지 않는다.

이제 원숭이는 머나먼 여행길을 떠난다. 격자판의 맨 왼쪽 위에서 시작해서 맨 오른쪽 아래까지 가야한다. 인접한 네 방향으로 한 번 움직이는 것, 말의 움직임으로 한 번 움직이는 것, 모두 한 번의 동작으로 친다. 격자판이 주어졌을 때, 원숭이가 최소한의 동작으로 시작지점에서 도착지점까지 갈 수 있는 방법을 알아내는 프로그램을 작성하시오.

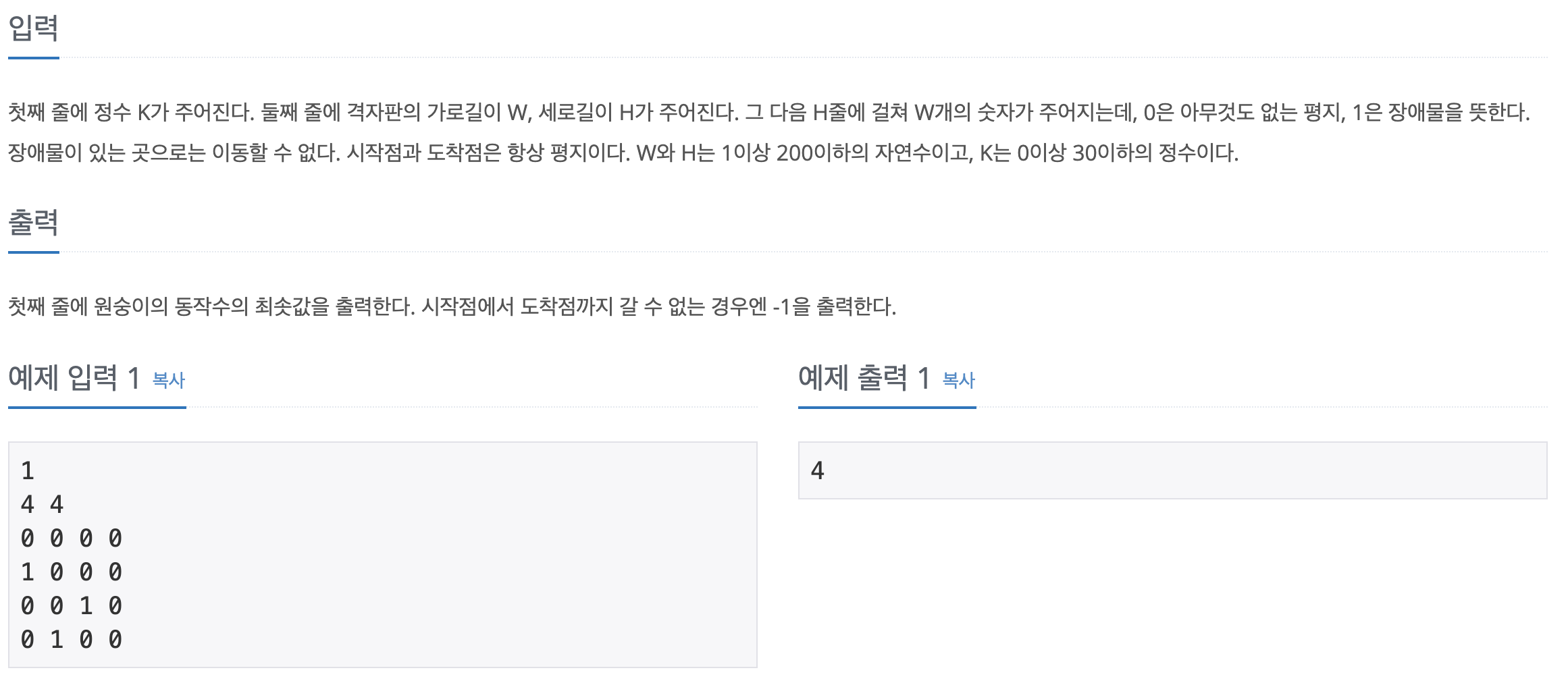
입출력

나의 풀이

위에서도 말했듯이 이 문제는 BOJ 2206 벽 부수고 이동하기 문제와 상당히 유사하다. BFS/DFS 와 DP 가 함께 사용되는 문제인데, 총 K번 사용할 수 있는 말 움직임 찬스를 관리하는 것이 핵심이었다.

나는 이번에도 뒤늦게 3차원 배열 사용을 알게되었는데,, 아,, 왜 그걸 생각 못했지,, ㅜㅡㅜ

처음에는 '최소 움직임'을 구해야 하는거니까 빨리 이동하는 말 찬스부터 먼저 사용하는 방식으로 작성했다. 하지만 이 경우는 일반 이동 이후에 말 이동이 필요한 경우를 커버할 수 없었다. 말 움직임을 먼저 사용하는 경우, 중간에 사용하는 경우, 뒤쪽에 사용하는 경우,, 여러 가지 경우의 수를 모두 커버하기 위해서는 방문 여부를 확인하는 visited 배열이 필연적으로 3차원이어야 한다는걸 깨달았다.

나는 visited배열에 H(세로) * W(가로) * K+1(말 이동 사용횟수) 로 3차원 공간을 할당했다.

여기서 처음에 난 3번째 공간을 K 개만 할당 했었는데, 이동시 말을 사용하는 횟수는 0번 ~ K번 까지 가능하므로 visited의 3번째 배열에는 총 K+1 개의 공간이 필요한 것이다!! 즉, H*W 개만큼 할당된 2차원 배열이 총 K+1 개가 필요하다!!

BFS에 사용되는 queue의 자료형은 <<int, int>, int> 로 하여 각 지점의 좌표(row, col) 과 해당 시점까지의 이동 중 말이동을 사용한 횟수를 함께 적용하였다.

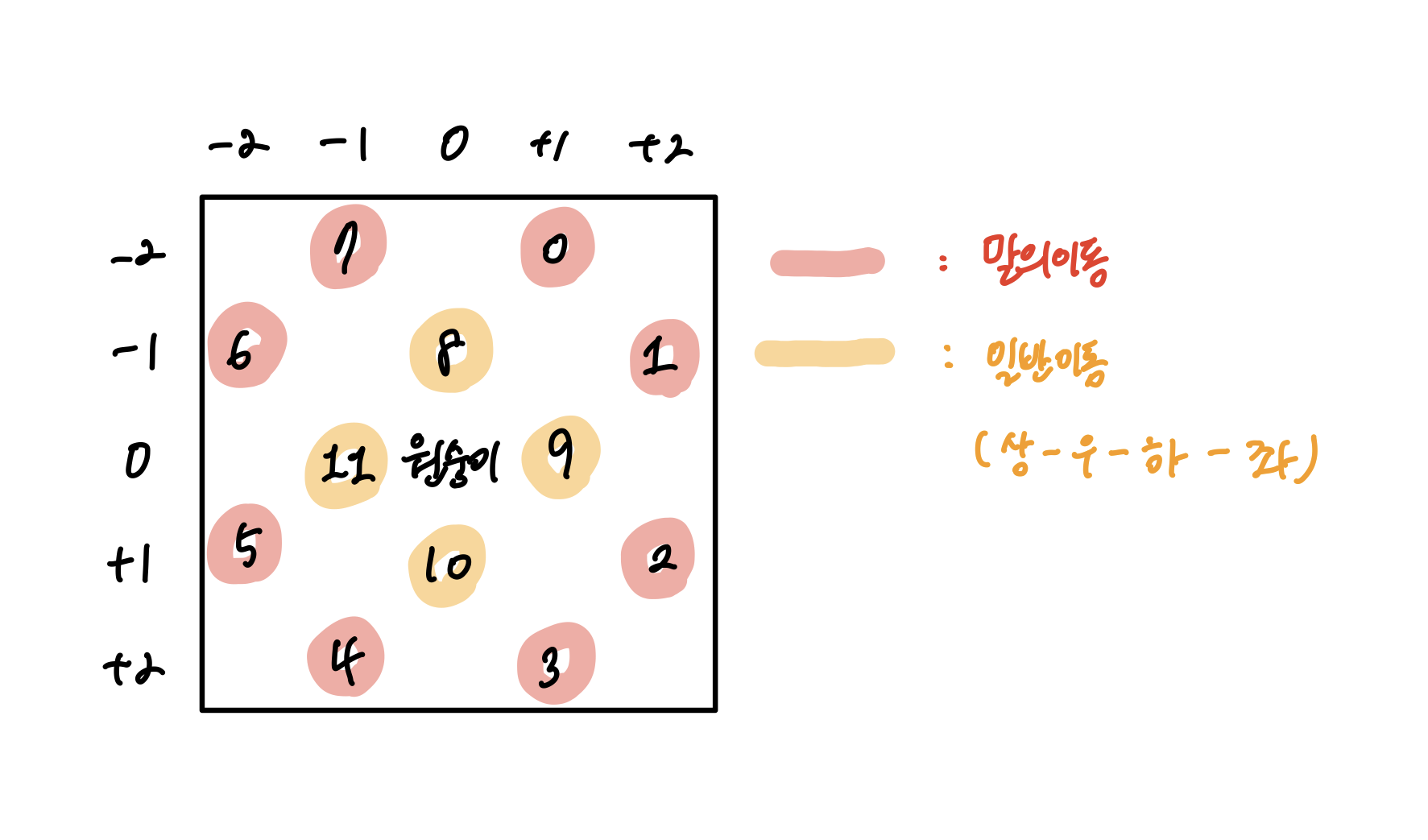
움직임은 위 그림과 같이 말의 이동과 일반적인 이동을 순서대로 dy[12], dx[12] 배열에 이동되는 좌표 값을 정해두고 사용했고,
dy[12], dx[12] 를 순회하면서 index가 0~7 일땐 말의 이동이 가능한지, 8~11 일땐 일반이동이 가능한지 확인하여 queue에 push 해주었다.

queue에서 ((row, col), k)를 꺼낼 때 마다 visited[row][col][k] 값이 최소값인지 확인하면서 queue가 빌때까지 모든 과정을 반복하였다!

코드

#include <iostream>
#include <vector>
#include <queue>

// 2147483647
// BOJ 1600 말이 되고픈 원숭이, 골드 4, 유사문제 boj 벽 부수고 이동하기
using namespace std;

int dy[12] = {-2, -1, 1, 2, 2, 1, -1, -2, -1, 0, 1, 0};
int dx[12] = {1, 2, 2, 1, -1, -2,-2, -1, 0, 1, 0, -1};

int getMinStep(vector<vector<int>> map, int K){
    bool able = false;  // 도달 가능한지

    int MIN = 2147483647;
    int H = map.size();
    int W = map[0].size();

    pair<int, int> destination = make_pair(H-1, W-1);

    // 현재까지의 이동 수 기록 & 방문 여부 체크용 3차원 배열, 말을 k번 사용해서 이동한 비용은  visited[y][x][k]에 저장된다.
    vector<vector<vector<int>>> visited(H, vector<vector<int>>(W, vector<int>(K+1, 0)));

    queue<pair<pair<int, int>,  int>> points;
    points.push(make_pair(make_pair(0,0), 0));
    visited[0][0][0] = 0;

    while (!points.empty()){
        // 현재 지점
        pair<pair<int, int>, int> loc = points.front();
        points.pop();

        // 목적지인지 확인, 최소 비용 갱신
        if (loc.first == destination){
            if (MIN > visited[loc.first.first][loc.first.second][loc.second]){
                MIN = visited[loc.first.first][loc.first.second][loc.second];
            }
            if (!able) able = true;
            continue;
        }

        // 0-7 : 말 이동 8가지  +  8-11 : 일반이동 4가지 확인
        for (int i = 0; i < 12; ++i) {
            int r = loc.first.first + dy[i];
            int c = loc.first.second + dx[i];

            // 지도 범위 내, 빈칸인지 확인
            if (r>=0 && r<H && c>=0 && c<W && map[r][c] == 0){
                if (i < 8){
                    // 말 이동 가능 & 방문 할 수 있는 곳이면
                    if (loc.second < K && visited[r][c][loc.second+1] == 0){
                        // 말 사용횟수 추가 (loc.second + 1)
                        visited[r][c][loc.second+1] = visited[loc.first.first][loc.first.second][loc.second] + 1;
                        points.push(make_pair(make_pair(r,c), loc.second+1));
                    }
                }else{
                    // 방문할 수 있는 곳이면
                    if (visited[r][c][loc.second] == 0){
                        // 말 사용 횟수 유지 (loc.second)
                        visited[r][c][loc.second] = visited[loc.first.first][loc.first.second][loc.second] + 1;
                        points.push(make_pair(make_pair(r,c), loc.second));
                    }
                }
            }

        }
    }

    if (able) return MIN;
    else return -1;
};

int main() {
    ios_base::sync_with_stdio(false);
    cin.tie(nullptr);
    cout.tie(nullptr);

    int K, W, H;
    cin>>K>>W>>H;

    vector<vector<int>> map(H, vector<int>(W,0));

    for (int i = 0; i < H; ++i) {
        for (int j = 0; j < W; ++j) {
            cin>>map[i][j];
        }
    }

    int step = getMinStep(map, K);
    cout<<step;

    return 0;
}

다음엔.. 한번만 더 생각해보자..! 3차원 배열..!!!!!