BOJ 20444 색종이와 가위
이분탐색 문제이고 골드 5의 난이도!
생각치 못했던 부분을 기록할만 해서 남겨본다
BOJ 20444 색종이와 가위
오늘도 역시 준성이는 어김없이 색종이와 쿼리를 푸는 데 실패하였다!!
색종이에 열등감을 느낀 준성이는 가위로 눈에 보이는 색종이를 모두 잘라 버리려고 한다!!
색종이를 자를 때는 다음과 같은 규칙을 따른다.
색종이는 직사각형이며, 색종이를 자를 때는 한 변에 평행하게 자른다.
자르기 시작했으면, 경로 상의 모든 색종이를 자를 때까지 멈추지 않는다.
이미 자른 곳을 또 자를 수 없다.
분노에 찬 가위질을 하던 준성이는 갑자기 하나의 색종이를 정확히 n번의 가위질로 k개의 색종이 조각으로 만들 수 있는지 궁금해졌다.
궁금하지만 화가 나서 코딩에 집중할 수 없는 준성이 대신 코드를 작성해주도록 하자.
입출력
[입력]
첫 줄에 정수 n, k가 주어진다. (1 ≤ n ≤ 231-1, 1 ≤ k ≤ 263-1)
[출력]
첫 줄에 정확히 n번의 가위질로 k개의 색종이 조각을 만들 수 있다면 YES, 아니라면 NO를 출력한다.
풀이

먼저 4번을 자른 맨 오른쪽 그림에서 가로로 자른 횟수 a, 세로로 자른 횟수 b 라 할 때 (a+1) * (b+1) 이 최종적인 색종이 조각 수를 나타내는 것을 알아내는 것이 가장 키 포인트였던 것 같다. 물론 난 몰랐음
그럼 결국 (a+1) * (b+1) = k 이면서 a+b = N 인 경우가 존재하는지를 확인하는 이차 방정식 문제로 생각할 수 있다.
b = N-a 를 대입하면 y = (a+1)(N-a+1) 이라는 a 에 대한 이차 함수가 완성 이 이차 함수와 y=k 라는 직선과의 교점이 존재하는 지 여부가 문제에 대한 답이 된다.
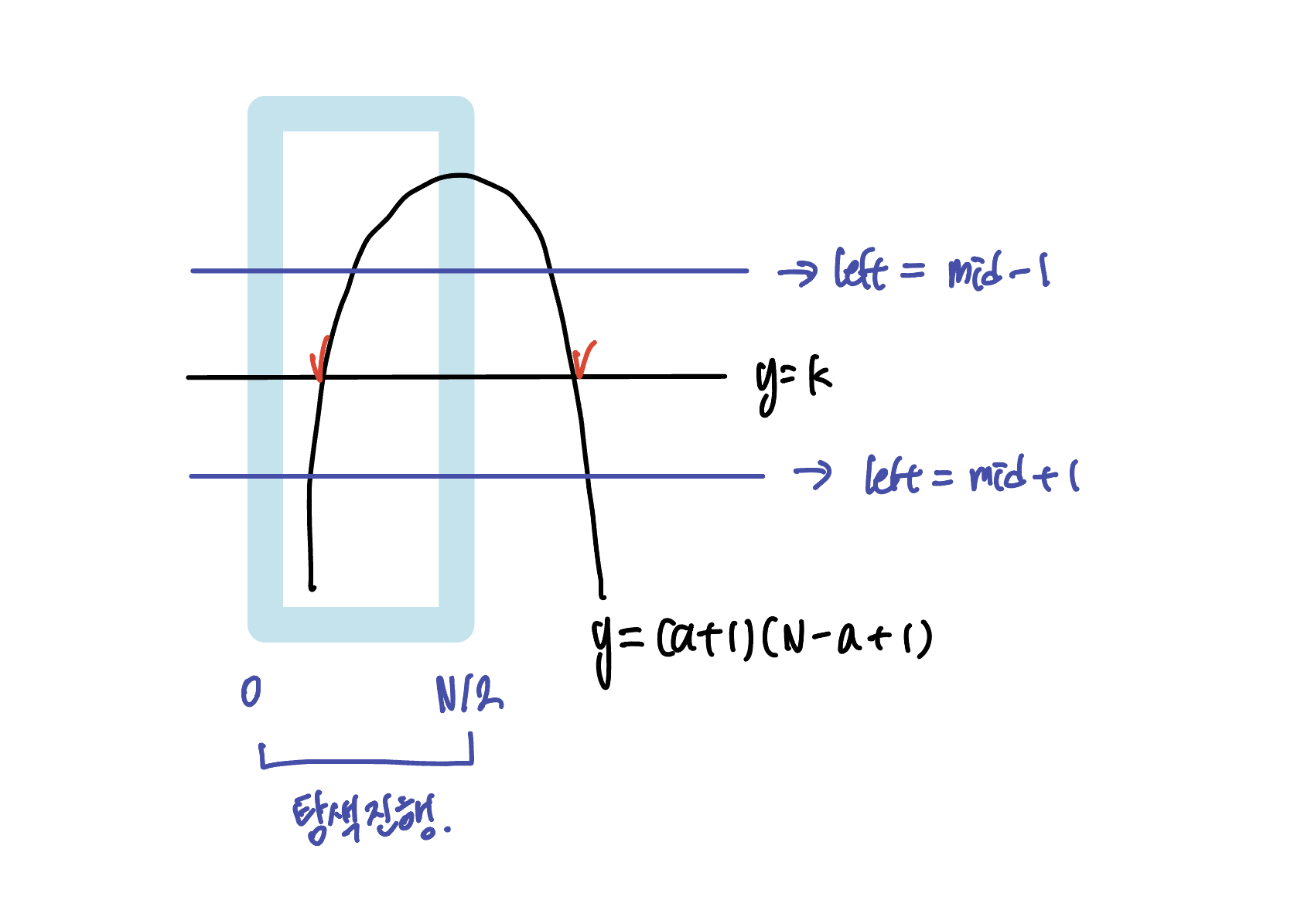
두 근 a, N-a 중 a 만 알면 되기 때문에 [0,N/2] 내에서 조건을 만족하는 a 에 대한 이분 탐색을 진행한다.
- mid 값을 (left + right) / 2 로 구하고
- 이차 함수에 대입한 값이
- k 보다 크다면 y=k 라는 직선보다 위쪽에 위치하기 때문에 왼쪽 근의 위치를 줄여준다.
- k 보다 작다면 y=k 라는 직선보다 아래쪽에 위치하기 때문에 왼쪽 근의 위치를 키워준다.
- left, right 가 역전 되지 않고 범위 내 근을 찾는다면 YES, 찾지 못한다면 NO 를 출력한다.
코드
import Foundation
// boj 20444 색종이와 가위, 이분 탐색, 골드 5
let str = readLine()!.split(separator: " ").map{Int($0)!}
let N = str[0]
let K = str[1]
var answer = "NO"
var left = 0
var right = N/2
while left<=right {
let x = (left+right)/2
let y = N-x
let frags = (x+1)*(y+1)
if frags<K {
left = x+1
} else if frags>K {
right = x-1
} else {
answer = "YES"
break
}
}
print(answer)
