[알고리즘 풀이 분석] BOJ 22858 원상복구

오랜만에 다시 푸는 알고리즘! 간단한 구현 문제 BOJ 22858 원상복구를 풀어보았다!

BOJ 22858 원상복구

수가 적혀있는 $P_1, P_2, ..., P_N$ $N$개의 카드가 있다.

1부터 N까지 수가 하나씩 존재하는 $D_1, D_2, ... , D_i , ... D_N$ 가 있다. 이때 $D_i$는 $P_{D_i}$ 값을 $i$ 번째로 가지고 오는 것을 의미한다. 이러한 작업을 카드 섞기라고 부른다. 카드를 섞는 작업은 동시에 진행된다.

예를 들어, $P_1, P_2, ..., P_N$이 1, 4, 5, 3, 2이고, $D_1, D_2, ..., D_N$가 4, 3, 1, 2, 5라고 가정해보자. 이 카드를 한번 섞으면 3, 5, 1, 4, 2가 된다. 아래 그림에서 $S$는 카드를 한 번 섞은 후를 의미한다.

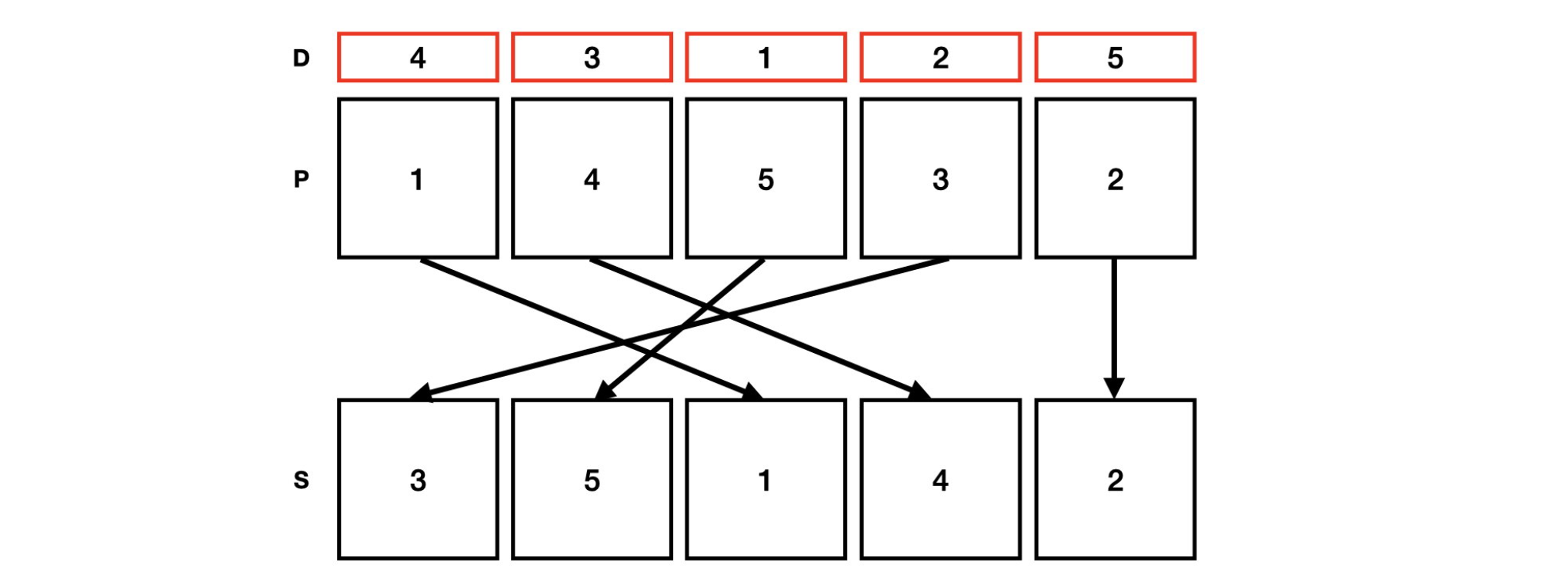
위 방식을 그대로 $K$번 섞은 카드의 정보와 $D$의 정보를 알고 있다고 할 때, 원래 카드는 어떤 배치를 이루고 있었는지 구해보자.

입출력

[입력]
첫번째 줄에는 카드의 개수 $N$과 카드를 섞은 횟수인 $K$가 공백으로 구분되어 주어진다.
두번째 줄에는 $K$번 카드를 섞은 후 카드의 배치를 의미하는 $S_i$가 공백으로 구분되어 총 $N$개 주어진다.
세번째 줄에는 총 N개의 $D_i$이 공백으로 구분되어 주어진다.

[출력]
원래 카드의 배치를 $P_1$부터 $P_N$의 값들을 공백으로 구분해서 출력한다.

[제한]
$1 \le N \le 10^4$ 
$1 \le K \le 10^3$ 
$1 \le D_i \le N$ 
$1 \le P_i, S_i \le 10^6$ 

나의 풀이

알고리즘 자체는 간단했다. 실버 3단계 문제였기 때문에 특별히 어려울 것은 없었다. 주어진 방식을 거꾸로 실행해보면 S[i] 값은 원래 D[i] 위치에 존재해야 한다는 것을 쉽게 알 수 있다!

입력으로 주어지는 S 배열을 k 번 거꾸로 돌려서 마지막 결과를 출력해주면 된다.

입력 값이 크다면 추가적인 배열을 쓰는 것을 고민했겠지만 그리 크지 않았기 때문에 매번 새로운 배열에 담은뒤 대체하는 형식으로 진행해주었다.

코드

#include <iostream>
#include <vector>

// boj 22858 원상 복구, 실버 3, 구현
using namespace std;

int main(){

    ios_base::sync_with_stdio(false);
    cin.tie(NULL);
    cout.tie(NULL);

    int N, K;
    cin>>N>>K;

    vector<int> S(N+1,0);
    vector<int> D(N+1, 0);

    for (int i = 1; i <= N; ++i) cin>>S[i];
    for (int i = 1; i <= N ; ++i) cin>>D[i];

    vector<int> rewind(N+1, 0);
    while (K>0){
        K--;
        for (int i = 1; i <= N; ++i) {
            int origin_index = D[i];
            int num = S[i];
            rewind[origin_index] = num;
        }

        S = rewind;
    }

    rewind.clear();

    for (int i = 1; i <= N; ++i) {
        cout<<S[i]<<' ';
    }
    cout<<'\n';

   return 0;
}