오늘 풀어본 문제는 BOJ 2961 도영이가 만든 맛있는 음식 이다.
완전 탐색 역시 심심치 않게 나오기 때문에 가볍게 한번 풀어보자 했는데, 완전 탐색 과정보다 문제를 푸는 과정에서 순열 조합 알고리즘을 한번 더 공부할 수 있는 기회였다!
순열 조함 알고리즘은 기본중의 기본이니까 라이브러리 없이도 구현할 수 있도록 해야겠다!
BOJ 2961 도영이가 만든 맛있는 음식
도영이는 짜파구리 요리사로 명성을 날렸었다. 이번에는 이전에 없었던 새로운 요리에 도전을 해보려고 한다.
지금 도영이의 앞에는 재료가 N개 있다. 도영이는 각 재료의 신맛 S와 쓴맛 B를 알고 있다. 여러 재료를 이용해서 요리할 때, 그 음식의 신맛은 사용한 재료의 신맛의 곱이고, 쓴맛은 합이다.
시거나 쓴 음식을 좋아하는 사람은 많지 않다. 도영이는 재료를 적절히 섞어서 요리의 신맛과 쓴맛의 차이를 작게 만들려고 한다. 또, 물을 요리라고 할 수는 없기 때문에, 재료는 적어도 하나 사용해야 한다.
재료의 신맛과 쓴맛이 주어졌을 때, 신맛과 쓴맛의 차이가 가장 작은 요리를 만드는 프로그램을 작성하시오.
입출력

나의 풀이
문제 자체는 매우 간단하다.
특별한 알고리즘 없이 모든 경우의 수를 계산해서 각 경우마다 신맛과 쓴맛을 계산하고 그 차이가 가장 작은 경우를 return 하면 된다.
이 과정에서 자연스레 조합을 구하게 된다. N개의 음식 재료 중 r(1-N) 개를 선택하는 조합을 구한 뒤 각 조합에 대해 신맛과 쓴맛을 계산해주어야 한다.
코드
#include <iostream>
#include <vector>
#include <stdlib.h>
#include <algorithm>
using namespace std;
// N개의 숫자 중 조합 구하기
vector<vector<int>> getCombinations(int N){
vector<vector<int>> combinations;
vector<int> candidates; // 0-1-2-3
for (int i = 0; i < N; ++i) {
candidates.push_back(i);
}
for (int i = 1; i <= N; ++i) {
// N개 중 i개 뽑을 때
vector<bool> take(N-i, false);
for (int j = 0; j < i; ++j) {
take.push_back(true);
}
do {
vector<int> indexes;
for (int k = 0; k < N; ++k) {
if (take[k]) indexes.push_back(candidates[k]);
}
combinations.push_back(indexes);
}while (next_permutation(take.begin(), take.end())); // 다음 순열이 있으면
}
return combinations;
}
int getBestTaste(int N, vector<pair<int, int>> ingredients){
vector<vector<int>> combinations = getCombinations(N); // 가능한 재료 조합을 모두 구함
int min = 2147483647;
for (int i = 0; i < combinations.size(); ++i) {
int sour = 1, bitter = 0;
// 각 조합별로 신맛, 쓴맛 계산
for (int j = 0; j < combinations[i].size(); ++j) {
int at = combinations[i][j];
sour *= ingredients[at].first;
bitter += ingredients[at].second;
}
// 신맛, 쓴맛 차이 계산 후 최솟값이면 갱신
int diff = abs(sour-bitter);
if (min > diff){
min = diff;
}
}
return min;
}
int main() {
int N, S, B;
vector<pair<int, int>> ingredients;
cin>>N;
for (int i = 0; i < N; ++i) {
cin>>S>>B;
ingredients.push_back(make_pair(S, B));
}
int answer = getBestTaste(N, ingredients);
cout<<answer;
return 0;
}여기서 핵심은 재료의 조합을 구하는 방법일텐데, 조합을 구현하는 방법은 크게 두가지로 나뉘는 것 같다!
algorithm 헤더의 next_permutation 함수를 사용하는 방법과, 사용하지 않고 직접 구현하는 방법이다.
조합(Combination) 구현 방법 1
먼저 next_permutation 를 사용하는 방법이다.
algorithm 헤더에 위치함 이 함수의 사용법을 먼저 알아야겠다
// 인자 1 - 구하고자 하는 순열의 시작, 인자 2 - 순열의 끝
bool next_permutation (BidirectionalIterator first, BidirectionalIterator last);
// 직접 비교함수 지정
bool next_permutation (BidirectionalIterator first, BidirectionalIterator last, Compare comp);
// 사용
int is_pemutaion_exist = next_permutation(array.begin(), array.end());next_permutation는 bool 값을 반환한다. 해당 배열에 또 다른 순열이 존재한다면 true, 그렇지 않다면 false 값을 반환한다.
만약, 배열 [1,2,3,4] 에 대해 해당 함수를 적용하면 1-2-3-4와 같은 순열 다음 1-2-4-3 과 같은 새로운 순열을 만든 뒤 true 값을 반환하는 것이다.
이를 이용해 조합을 구하면,
vector<vector<int>> getCombinations(int N){
vector<vector<int>> combinations;
vector<int> candidates; // 조합을 구할 대상 배열
for (int i = 0; i < N; ++i) {
candidates.push_back(i);
}
for (int i = 1; i <= N; ++i) { // N개 중 i개 뽑을 때
vector<bool> take(N-i, false);
for (int j = 0; j < i; ++j) {
take.push_back(true);
}
do {
vector<int> indexes;
for (int k = 0; k < N; ++k) { // take 값에 따라 해당 수를 뽑고,
if (take[k]) indexes.push_back(candidates[k]);
}
// 조합(indexes) 을 만들어 조합들의 집합 (combinations) 에 push
combinations.push_back(indexes);
}while (next_permutation(take.begin(), take.end())); // take를 새롭게 배열할 수 있으면 계속 진행
}
return combinations;
}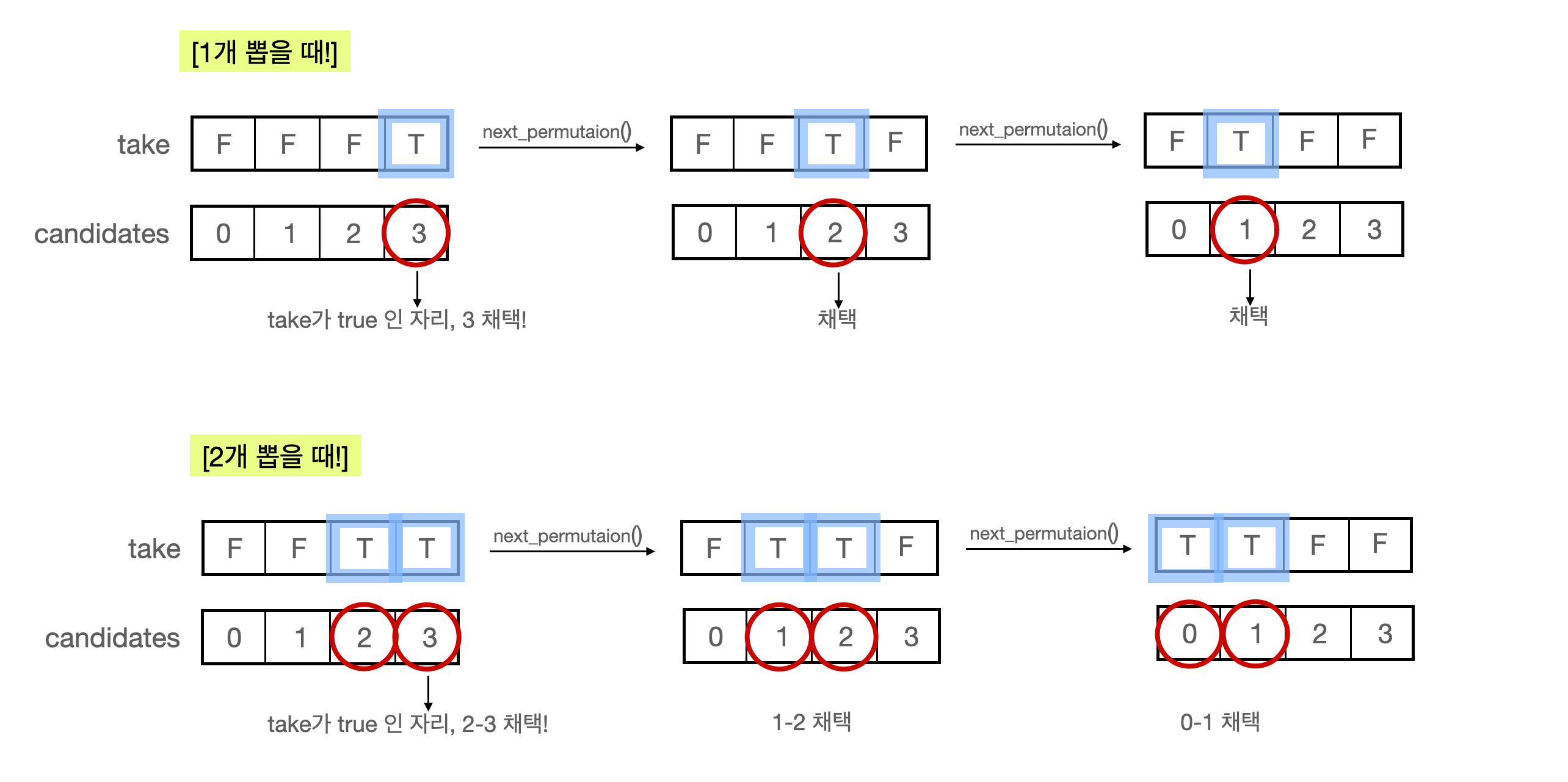
배열 candidates = [0,1,2,3] 을 이용해 조합을 구한다고 가정해보자.
그럼 이중에서 1개를, 2개를, 3개를, 4개를 뽑는 상황이 있을 것이다. 그럼 전체 원소 갯수(4개) 중에서 뽑고자 하는 갯수 (i) 개만 True 값을 갖도록 배열(take)을 생성한다.
이후 candidates 를 기준으로 고정시키고, next_permutation 함수를 사용하여 take 원소들의 자리를 바꾸는 것이다. 바뀔 때 마다 take 가 true인 자리의 candidates 원소를 조합에 포함시키고, false 이면 포함시키지 않으며 조합 (indexes)를 생성해 결과로 반환한 combinations에 push_back 시킨다!
조합(Combination) 구현 방법 2
이번엔 next_permutation 를 사용하지 않고 조합을 구현하는 방법이다.
재귀적으로 구현하는 방법이고, 사실 수의 크기가 커지면 시간 초과가 날 가능성이 크기 때문에 c++을 이용한다면 next_permutation를 사용하는 것이 안전한 것 같다.
문제 해결에는 next_permutation을 사용하였지만 이 방법 또한 알아두자.
이 방법은 nCr = n-1Cr-1 + n-1Cr 개념을 사용하는 것이다.
총 n개의 원소 (1번->n번) 중에서 r개를 뽑는다면 1번 원소를 뽑고 2번~n번 중에서(n-1개) r-1 개를 뽑는 경우 / 1번 원소를 뽑지 않고 2번~n번 중에서(n-1개) r 개를 뽑는 경우로 경우의 수가 나뉜다!
이 단순한 개념을 나타낸 공식이 nCr = n-1Cr-1 + n-1Cr 이고, 이를 이용해 조합을 구하는 알고리즘이다.
#include <iostream>
#include <vector>
using namespace std;
vector<vector<int>> result;
void combination(vector<int> arr, vector<int> comb, int r, int depth) {
if (r==0){
result.push_back(comb);
return;
}
// 원소를 다 뽑지 않고 끝난 경우
else if (depth == arr.size()) return;
else{
// arr[depth]를 뽑지 않은 경우
combination(arr, comb, r, depth+1);
// arr[depth] 를 뽑은 경우
comb.push_back(arr[depth]);
combination(arr, comb, r-1, depth+1);
}
}
int main() {
int N, R;
cin>>N>>R;
vector<int> array;
for (int i = 0; i < N; ++i) {
array.push_back(i+1);
}
vector<int> comb;
combination(array, comb, R,0);
return 0;
}- array : N개의 원소가 담긴, 조합을 구하는 대상 배열
- comb : 부분 조합을 완성해 나가는 배열
- depth : 현재 array 배열에서 탐색이 이루어지고 있는 원소의 위치 (2를 뽑을 지 말지를 결정중이라면 depth = 1)
5개 중 2개 뽑는 모든 조합을 출력하면,
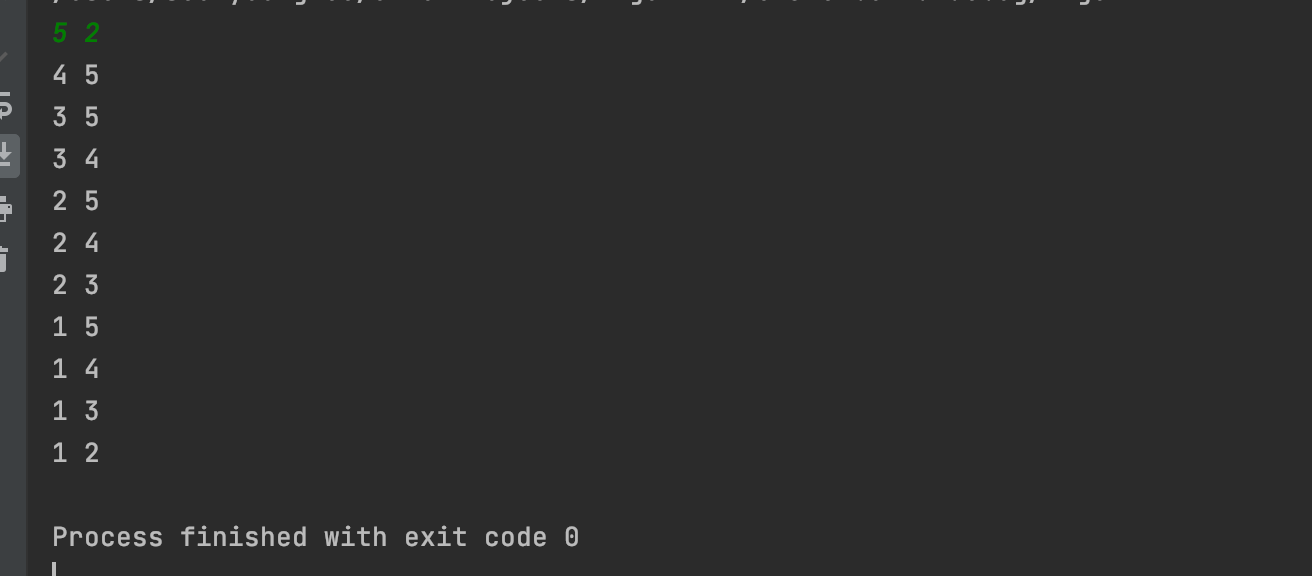
여기서 중요한 부분은 depth 가 가리키는 원소를 뽑는 경우보다 뽑지 않는 경우를 더 먼저 호출해야 한다는 점이다!
원소를 뽑는 경우 comb에 해당 원소를 담은 뒤에 다시 재귀적으로 함수를 호출하기 때문에 comb에 해당 원소가 포함되지 않은 상태로 뽑지 않는 경우의 재귀함수를 호출한 뒤, comb에 해당 원소를 담고 나머지 원소들을 채우러 재귀함수를 호출해야 한다!
재귀적으로 combination() 함수를 호출하는 방식이기 때문에 n, r이 커지면 시간초과가 날 수 있지만, 코딩테스트 마다 라이브러리를 사용하지 못하는 경우도 종종 있으니 알아두자!
(C++) 조합(Combination) 구현하기
[Algorithm] C++에서 next_permutation 함수(혹은 prev_permutation 함수)를 통해서 순열 구하기
