[알고리즘 풀이 분석] 프로그래머스 멀쩡한 사각형

오늘 풀어본 문제는 프로그래머스 멀쩡한 사각형 이다.
수학 문제였는데 풀이 자체는 굉장히 간단하다.
하지만 난 c++ 로 풀면서 자료형 때문에 아주,,ㅎㅎ 고생을 했다
별 지랄 발광을 해도 통과가 안되길래,, 도무지 이유를 모르겠어서 그냥 풀이를 바꿔서 통과했다,,! 마음이 너덜 너덜,, 하다 ㅋ

프로그래머스 멀쩡한 사각형

가로 길이가 Wcm, 세로 길이가 Hcm인 직사각형 종이가 있습니다. 종이에는 가로, 세로 방향과 평행하게 격자 형태로 선이 그어져 있으며, 모든 격자칸은 1cm x 1cm 크기입니다. 이 종이를 격자 선을 따라 1cm × 1cm의 정사각형으로 잘라 사용할 예정이었는데, 누군가가 이 종이를 대각선 꼭지점 2개를 잇는 방향으로 잘라 놓았습니다. 그러므로 현재 직사각형 종이는 크기가 같은 직각삼각형 2개로 나누어진 상태입니다. 새로운 종이를 구할 수 없는 상태이기 때문에, 이 종이에서 원래 종이의 가로, 세로 방향과 평행하게 1cm × 1cm로 잘라 사용할 수 있는 만큼만 사용하기로 하였습니다.
가로의 길이 W와 세로의 길이 H가 주어질 때, 사용할 수 있는 정사각형의 개수를 구하는 solution 함수를 완성해 주세요.

입출력

• W, H : 1억 이하의 자연수

W	H	result
8	12	80

나의 풀이

내가 처음 시도했던 풀이는 n번째 줄 마다 제외되는 칸 수를 수학적으로 계산해서 모든 칸 수에서 제외시켜 나가는 방법이었다.

예를 들어, 주어진 예제를 기준으로 하면

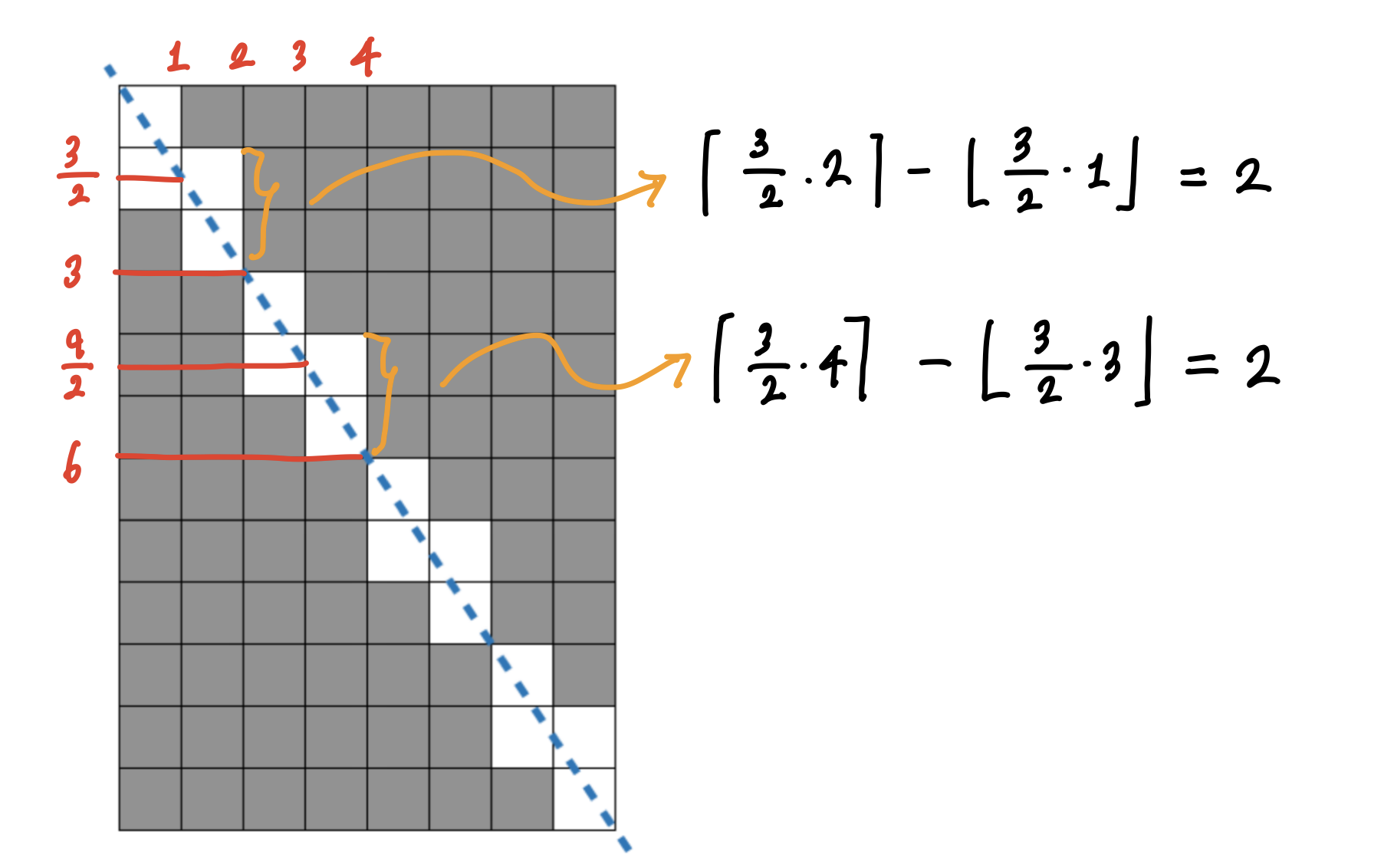
이런식으로 자르는 선의 기울기를 이용해 선이 통과하는 칸의 갯수를 수학적으로 연산하는 방법을 선택했다.

하지만 주어지는 w, h 가 모두 1억 이하의 자연수이고 반환 타입이 long long 이었기 때문에 overflow를 주의했어야 하는데 온갖 변수를 다 long long 으로 바꾸고 뭘 해봐도 12~17 테스트 케이스를 통과하지 못했다,, 하 왜인거지

결국 훨씬 간단한 방법을 참고해 겨우 통과 하였다.

주어지는 w, h 를 최대 공약수로 나누어w' h' 를 만들면 (8, 12 라면 w' = 2, h' = 3)

잘려 나가는 사각형의 모양들을 w'x h' 크기의 직사각형을 기준으로 반복되고 w'x h' 크기의 사각형에서 잘려나가는 격자의 수는w' + h' -1 개 이다.

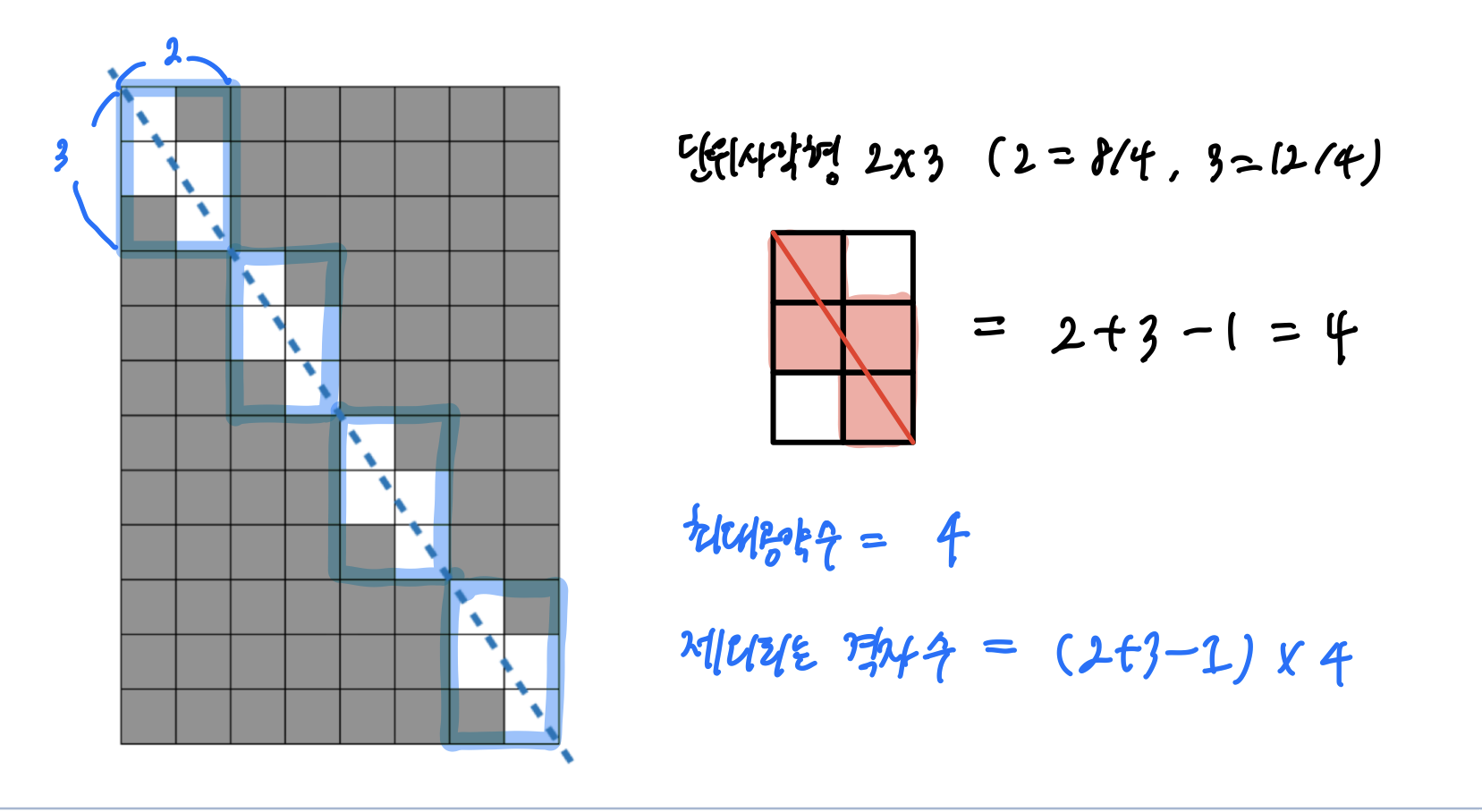
즉, 전체 w x h 크기의 사각형에서 w' + h' -1 개의 격자들이 최대 공약수 만큼 반복되어 잘려나가게 되는 규칙성을 가진다.

이를 이용하면 아주 간단해 진다.

살아남는 격자의 수 = w h - (w'+ h'-1) 최대 공약수

그런데 이때 w' = w / 최대 공약수, h'= h / 최대 공약수 이기 때문에 대입하면,

w h - (w'+h'-1) 최대 공약수 = w * h - (w + h - 최대 공약수)

가 최종적인 식이 된다.

오늘도 역시 swift 와 동시에 풀어봤다!

코드

cpp

#include <cmath>

using namespace std;

int getGCD(long long a, long long b){
    int small, big;
    if(a>b) { 
        big = a; 
        small = b;
    } else{
        big = b;
        small = a;
    }
    
    int mod = big%small;
    
    while(mod>0){
        big = small;
        small = mod;
        mod = big%small;
    }
    
    return small;
}

long long solution(int w,int h) {
    long long W = w;
    long long H = h;
    
    int gcd = getGCD(W, H);
    
    long long total = W*H;
    long long answer = total - (W+H-gcd);
    
    return answer;
}

swift

import Foundation

func getGCD(_ a : Int64, _ b : Int64) -> Int64 {
    var big : Int64 = 0
    var small : Int64 = 0
    
    if(a<b){
        big = b
        small = a
    }else{
        big = a
        small = b
    }
    
    var mod = big % small
    
    while(mod>0){
        big = small
        small = mod
        mod = big%small
    }
    
    return small
    
}

func solution(_ w:Int, _ h:Int) -> Int64{
    
    var answer:Int64 = 0
    var W = Int64(w)
    var H = Int64(h)
    let total = W*H
    let gcd = getGCD(W, H)
    
    return total - (W + H - gcd)
}