선택정렬, 삽입정렬, 셀 정렬

선택 정렬(select sort)

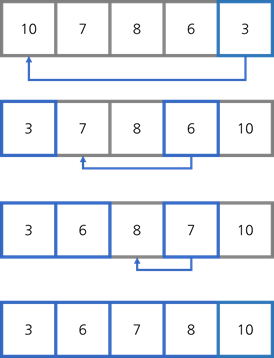
선택 정렬은 순서대로 리스트의 가장 작은 수를 찾고 그 수를 확정되지 않은 부분의 가장 앞 자리에 놓는 방법 으로 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬이다.

위 그림을 보면 10에서부터 시작해 리스트를 탐색해가면서 가장 작은 수인 3을 찾아서 10과 자리를 교체했다.
그리고 7로 넘어가서 8, 6, 10 중에 가장 작은 수인 6을 찾아 7과 자리를 교체했다.

맨 앞부터 시작해서 n번째 요소까지 n-1번 대소 비교를 하고 그 이후는 n-2번, n-3번, ... , 1번 비교하기 때문에 이들을 모두 합하면, 복잡도는 $O( n^2)$이 된다.
리스트가 이미 정렬되어 있다고 하더라도 대소 비교를 해야 하므로 최선, 최악, 평균의 경우 모두 $O( n^2)$이다.

---

삽입 정렬(Insertion sort)

삽입 정렬은 요소를 하나씩 꺼내서 그 요소 앞에 있는 다른 요소들과 모두 비교하는 방법으로 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬이다.

위 그림을 보자
첫번째 요소인 7은 그대로 두고 두번째 요소 8을 꺼내서 7과 비교한다.
7이 8보다 작으므로 그대로 둔다.

그리고 세번째 요소인 6을 꺼내서 8과 비교한다.
6이 8보다 작으므로 6과 8의 자리를 바꾸고 6을 다시 7과 비교한다.
6이 7보다 작으므로 6과 7의 자리도 바꾼다.

이렇게 마지막 요소까지 앞에있는 요소과 비교를 하면 정렬이 끝난다.

삽입 정렬은 이미 잘 정렬된 딕셔너리나 데이터베이스에 몇가지의 요소만 추가할 때 사용한다.
이미 순서에 맞게 잘 정리되어있으면 모든 요소를 각각 1번씩 n-1번만 비교하면 되기 때문이다.
미 정렬이 잘 된 부분은 다시 정렬할 필요가 없기 때문에 복잡도가 $O(n)$에 가깝다.

하지만 최악의 경우 두번째 요소가 1번 대소비교를 하고 그 이후부터 2번, 3번 ... n-1번 비교해야하기 때분에 복잡도가 $O( n^2)$ 이된다.

// 첫번째 요소는 건너 뜀 -> i가 1로 시작
for (int i=1; i < array.length; i++) {
	int j;
    
    // 각각의 요소를 v에 저장
	v = array[i]; 
    
    // 현재 요소보다 앞에 있는 요소를 하나씩 모두 탐색
	for (int j=i-1; j >= 0; i--) {
    
		// v가 바로 전의 요소보다 크거나 같으면 break
		if (array[j] <= v){
			break;
		}
        
        // v가 바로 전의 요소보다 작으면 위치를 바꿔줌
		array[j+1] = array[j];
	}
	array[j+1] = v;
}

---

셀 정렬(Shell sort)

셀 정렬은 일정한 너비만큼 떨어진 요소를 가져와서 그 둘을 대소비교한 후 바꾸는 방법이다. 처음에는 큰 간격으로 시작해서 더 적은 간격으로 정렬을 하고 간격의 크기가 1이 되면 삽입 정렬을 한다.

즉, 셀 정렬은 작은 값을 가진 요소는 오른쪽에서 왼쪽으로 옮기고 큰 값을 가진 요소는 왼쪽에서 오른쪽으로 옮기는 알고리즘이다.

셀 정렬은 중복된 숫자의 순서가 보장되지 않는 불안정 정렬이며 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬이다.

최악의 경우, 삽입 정렬과 같아지므로 복잡도는 $O( n^2)$지만, 셀 정렬의 평균적인 시간 복잡도는 얼마의 간격을 사용했는지에 따라 달라진다.