자바로 구현하고 배우는 자료구조
1.자바 특성 및 알고리즘 기본

많은양의 데이터를 어떻게 컴퓨터가 효율적으로 처리하는 지 알기 위해선 자료구조에 대한 이해가 필요합니다
2.LinkedList와 addFirst 메소드
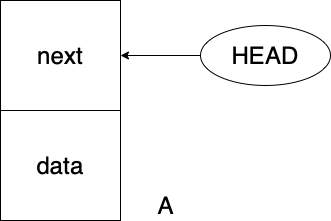
연결리스트와 addFirst
3.addLast 메소드
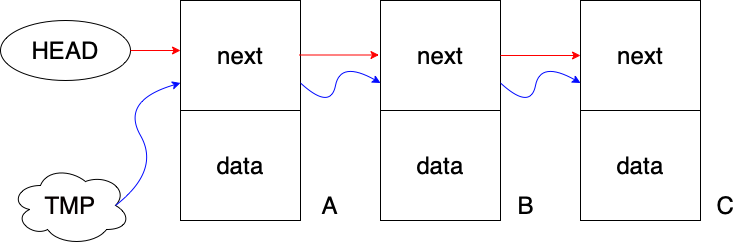
addLast 메소드에서는 연결 리스트의 마지막을 가리키는 임시 포인터를 사용합니다.
4.removeFirst메소드와 removeLast메소드
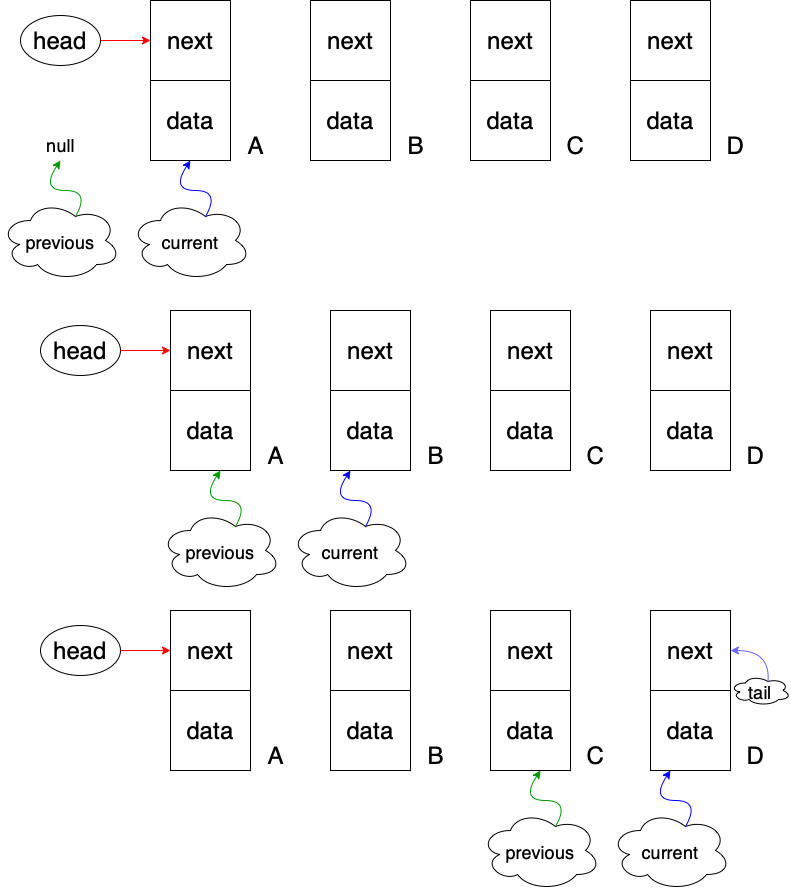
removeFirst. removeLast
5.find 메소드
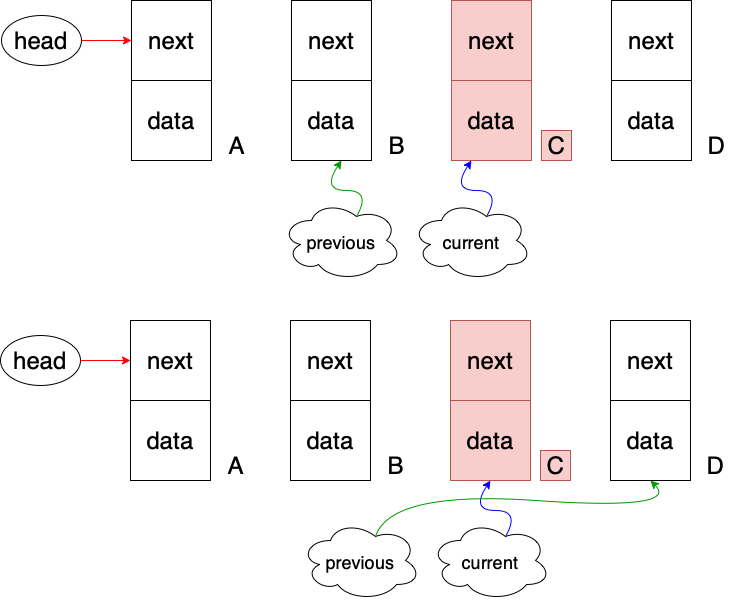
특정위치의 노드를 제거하고 싶을 땐, 먼저 특정위치가 어디인지 먼저 찾아야합니다.
6.peek 메소드

peek는 요소의 내용을 알 수 있습니다.
7.Iterator 인터페이스

Iterator 인터페이스
8.Double Linked List
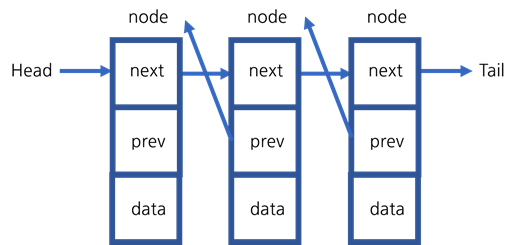
이중 연결 리스트
9.Circular Linked List
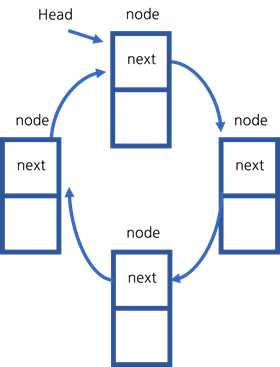
원형 연결 리스트는 마지막 next 포인터가 연결 리스트의 노드를 가리키는 연결 리스트입니다.
10.스택과 큐

스택과 큐를 구현하는 경우 배열과 리스트의 차이점
11.Hash
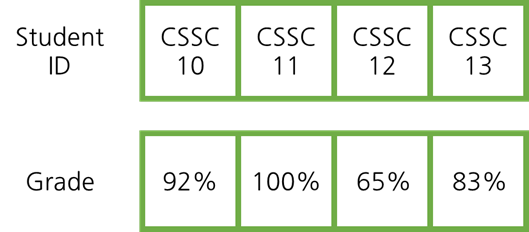
요소를 빠르게 찾거나, 삭제, 추가를 할 수있는 자료구조에 대해 알아보겠습니다.
12.체이닝 (Chaining)
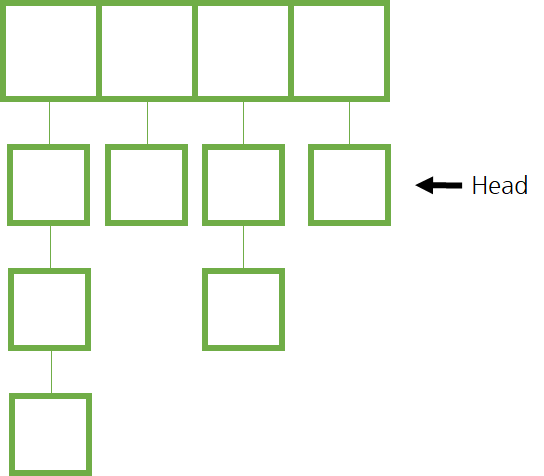
체이닝은 이 배열의 위치마다 새로운 자료구조를 만들어 수많은 데이터를 수용할 수 있도록 만들어 줍니다.
13.해시클래스

배열과 배열의 요소가 리스트로 이루어진것을 체인해시라고 합니다. 이 해시는 키를 기반으로 저장이되어있습니다.
14.Hash - add, remove, getValue, resize, key 반복자

해시에 무언가를 추가하거나 제거하는 add, remove메소드를 만들어보겠습니다.
15.힙과 트리
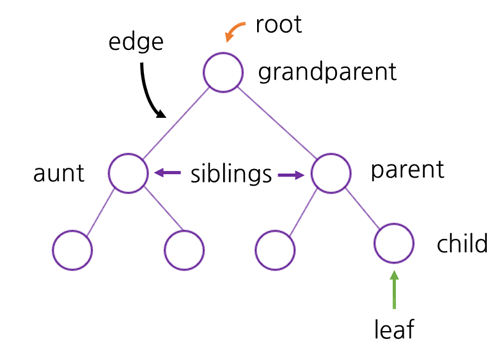
노드를 나무 형태로 연결한 구조를 트리라고 합니다.
16.힙 추가와 제거
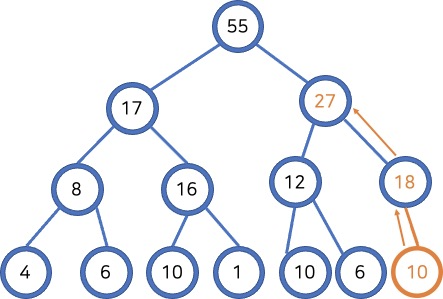
힙에 새로운 데이터를 추가하거나 제거할 때 힙의 규칙을 지켜야 합니다.
17.완전 트리와 정 트리
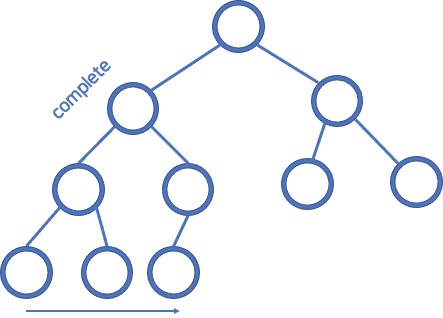
완전 트리 (Complete Tree): 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 마지막 줄은 왼쪽에서 오른쪽 순서로 채워져 있는 트리입니다. 정 트리 (Full Tree): 모든 잎이 아닌 노드가 2개의 자식 노드를 가지고 있고 모든 잎이 같은 레벨에 있는 트리입니다.
18.트리 - 순회
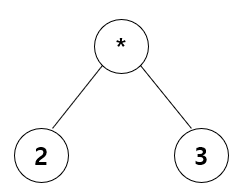
트리의 노드를 방문하는 방법을 트리 순회라고 합니다.
19.트리 - 노드 클래스, add, contains
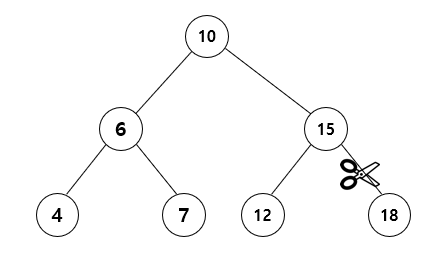
노드 클래스 위의 그림처럼 트리는 항상 작은 값이 왼쪽에 와야합니다. 그렇기 때문에 어떤 값을 찾고싶다면 루트의 값보다 큰지 작은지 확인을 해야합니다. 이렇게 위에서부터 비교를 하며 내려가면 남은 데이터의 반은 항상 무시하고, 간 복잡도는 $log n$를 가집니다. 연결리스트가 next 포인터를 가지는 것처럼 트리는 parent, left, righ...
20.트리 - 회전

아래와 같이 한 방향으로 나열된 트리를 균형 잡히지 않은 트리라고 합니다.
21.AVL 트리
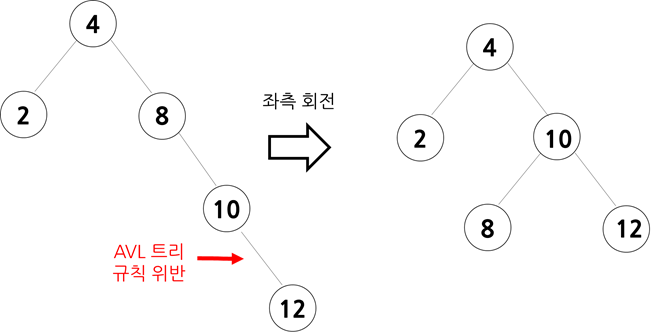
AVL트리는 왼쪽과 오른쪽의 높이 차이가 항상 1보다 작거나 같아야합니다.
22.레드-블랙트리

레드-블랙트리는 AVL트리처럼 스스로 균형을 잡는 자가 균형 이진 탐색트리다.
23.레드-블랙트리 구현

add 메소드 레드-블랙트리에 요소를 추가하려면 먼저 루트가 비어있는지 확인을 해야한다. 레드-블랙트리에는 지켜야할 규칙이있다. 그러므로 요소를 추가한 이후에 규칙을 모두 만족했는지 다시 확인해야한다. 규칙이 지켜지지 않았다면 트리를 다시 조작해 노드를 올바른 위치
24.정렬이란 ?
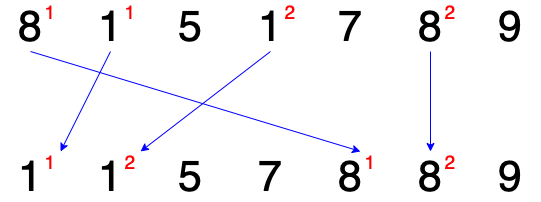
데이터를 정렬해야하는 경우는 매우 많고 정렬를 하는 방식도 매우 다양하다.
25.선택정렬, 삽입정렬, 셀 정렬
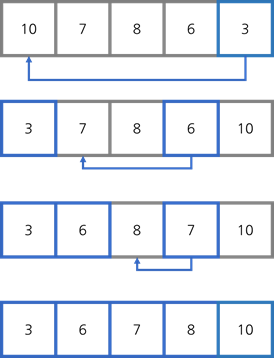
선택 정렬(select sort) 선택 정렬은 순서대로 리스트의 가장 작은 수를 찾고 그 수를 확정되지 않은 부분의 가장 앞 자리에 놓는 방법 으로 리스트 안에서 순서만 바꿔주기 때문에 in-place 정렬이다. 위 그림을 보면 10에서부터 시작해 리스트를 탐색해가면서 가장 작은 수인 3을 찾아서 10과 자리를 교체했다. 그리고 7로 넘어가서 8, 6,...
26.합병 정렬, 퀵 정렬, 기수 정렬
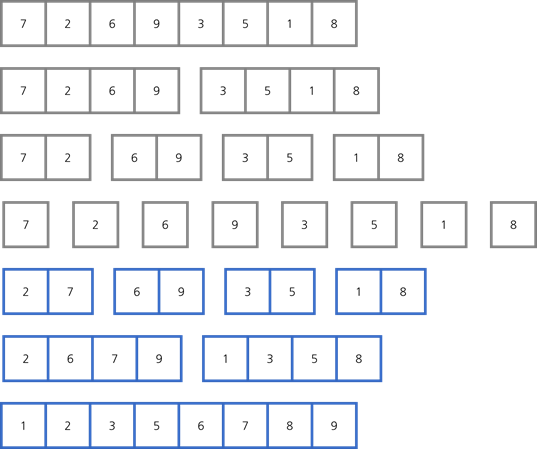
합병 정렬 (Merge sort) 합병 정렬은 요소가 하나만 남을 때까지 리스트를 반으로 나눠준 후, 나눴던 리스트를 대소 관계에 맞게 다시 합치는 방법이다. 위 사진에서는 모든 리스트의 요소가 하나가 될 때까지 나누고 2와 7을 붙이기 위해 대소 비교를한다. 2가