[최적화이론] Binary Cross Entropy와 Softplus

Ethan·2023년 4월 4일
BCEsoftplus최적화이론
1

최적화이론

목록 보기
5/5

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 언제든지 댓글 남겨주세요.

일반적으로 binary classification에서는 loss function으로 Binary Cross Entropy Loss (BCE loss)를 사용합니다. 그런데 정작 모델 코드를 뜯어보면 BCE loss가 아니라 softplus function을 쓰는 경우가 있습니다. 대표적으로 Forward Forward algorithm 구현 코드가 그렇습니다.

왜 그럴까요?

Softplus, Sigmoid, Softmax

Softplus는 activation function의 일종입니다. 수식으로 나타내면 다음과 같습니다.

Softplus ζ(x)=1βlog⁡(1+exp⁡(β⋅x))(1)\text{Softplus}\ \zeta(x)={1\over\beta}\log(1+\exp(\beta\cdot x))\qquad(1)

softplus의 그래프는 다음과 같습니다.

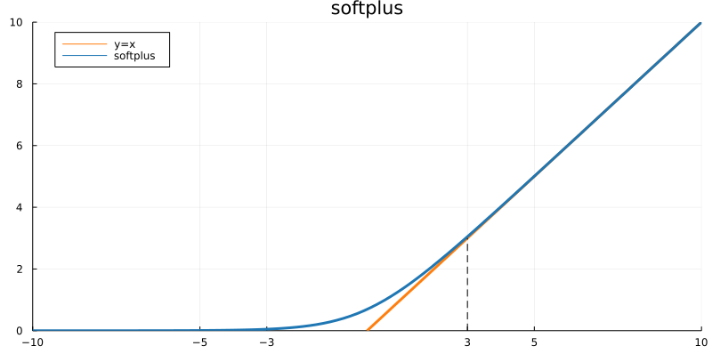
딱 봐도 ReLU와 매우 비슷하게 생겼습니다. 0에서 미분가능한 ReLU로 취급해도 무방하고, (−3,3)(-3, 3) 구간 밖에서는 ReLU와 거의 동일합니다. 출력값이 항상 양수라는 점에서 ReLU의 대체재로도 종종 사용합니다.

그런데 식 (1)을 보면 생각나는 수식 2가지가 있습니다. 바로 Sigmoid와 Softmax입니다.

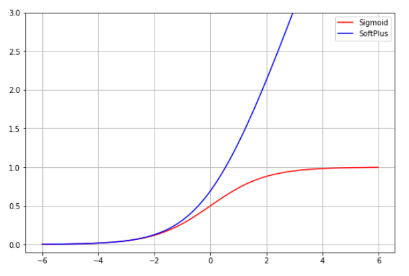
Sigmoid=11+exp⁡(−x),Softmax=exp⁡(xi)∑i=1kexp⁡(xi)\text{Sigmoid} = {1\over1+\exp(-x)},\quad\text{Softmax}={\exp(x_i)\over\sum_{i=1}^k\exp(x_i)}

딱 봐도 softplus와 모종의 관계가 있을 것처럼 생겼죠? softmax는 sigmoid의 일반화 버전이니, sigmoid와 softplus의 관계를 알 수 있다면 softmax에도 적용할 수 있을 것 같습니다. 과연 두 함수 사이에는 어떤 관계가 있을까요?

Softplus를 미분하면 Sigmoid

결론부터 말하자면, β=1\beta=1일 때 softplus를 미분하면 sigmoid가 됩니다.

∂∂xζ(x)=∂∂x(1βlog⁡(1+exp⁡(β⋅x)))=∂∂xlog⁡(1+exp⁡(x))=exp⁡(x)1+exp⁡(x)=11+exp⁡(−x)\begin{aligned} {\partial\over\partial x}\zeta(x) &={\partial\over\partial x}\left({1\over\beta}\log(1+\exp(\beta\cdot x))\right)\\ \quad\\ &={\partial\over\partial x}\log(1+\exp(x))\\ \quad\\ &={\exp(x)\over1+\exp(x)}={1\over 1+\exp(-x)} \end{aligned}

그럼 sigmoid에 log를 씌우면?

그렇다면 sigmoid에 log를 씌우면 어떻게 될까요?

log⁡(11+exp⁡(−x))=log⁡1−log⁡(1+exp⁡(−x))=−log⁡(1+exp⁡(−x))=−ζ(−x)(2)\begin{aligned} \log\left({1\over 1+\exp(-x)}\right)&=\log1-\log(1+\exp(-x))\\ \quad\\ &=-\log(1+\exp(-x))\\ \quad\\ &=-\zeta(-x)\qquad(2)\\ \end{aligned}

중요한 성질이니 식 (2)를 잘 기억해둡시다. 참고로 다음과 같은 성질들도 성립합니다.

(1) ζ(x)−ζ(−x)=x\zeta(x)-\zeta(-x)=x

(2) ζ−1(x)=log⁡(exp⁡(−x)−1),∀x>0\zeta^{-1}(x)=\log(\exp(-x)-1),\quad\forall x>0

BCE Loss와 Softplus

이제 이번 포스팅의 핵심인 Softplus와 Binary Cross Entropy Loss(BCE loss)의 관계에 대해 살펴보겠습니다. 먼저 BCE 수식은 다음과 같습니다.

BCE={−log⁡y^,where  y=1(3)−log⁡(1−y^),where  y=−1(4)BCE= \begin{cases} -\log\hat y, & \text{where}\ \ y=1\qquad(3)\\ -\log(1-\hat y), & \text{where}\ \ y=-1\qquad(4) \end{cases}

식 (3)은 모델이 예측한 y=positivey=\text{positive}일 log probability이고, 식 (4)는 모델이 예측한 y=negativey=\text{negative}일 log probability입니다. 따라서 엔트로피의 정의를 이용하여 위 식을 다시 아래와 같이 일반적으로 사용하는 BCE Loss 형태로 바꿀 수 있습니다.

위 식은 positive가 target label이라는 점을 기억합시다.

BCE=H(y=1)+H(y=−1)=Ey=1[−log⁡y^]+Ey=−1[−log⁡(1−y^)]=−[py=1log⁡y^+py=−1log⁡(1−y^)]=−py=1log⁡y^−(1−py=1)log⁡(1−y^)\begin{aligned} BCE&=H(y=1)+H(y=-1)\\ \quad\\ &=E_{y=1}[-\log\hat y]+E_{y=-1}[-\log(1-\hat y)]\\ \quad\\ &=-[p_{y=1}\log\hat y+p_{y=-1}\log(1-\hat y)]\\ \quad\\ &=-p_{y=1}\log\hat y-(1-p_{y=1})\log(1-\hat y) \end{aligned}

만약 N개의 데이터가 있다면, 전체 데이터의 평균 BCE loss는 다음과 같이 나타낼 수 있겠죠.

BCEN=−1N∑iN(py=1log⁡y^+(1−py=1)log⁡(y^))(5)BCE_N=-{1\over N}\sum_i^N\left(p_{y=1}\log\hat y+\right(1-p_{y=1})\log(\hat y))\qquad(5)

Can we use softplus instead?

자, N개의 데이터가 주어진 상황을 다시 가정해봅시다.

BCE=−∑N(plog⁡y^+(1−p)log⁡(1−y^))=−∑Nplog⁡y^−∑N(1−p)log⁡(1−y^)=−∑Nplog⁡(σ(z))−∑N(1−p)log⁡(1−σ(z))(6)\begin{aligned} BCE&=-\sum^N\left(p\log\hat y+\right(1-p)\log(1-\hat y))\\ \quad\\ &=-\sum^Np\log\hat y-\sum^N(1-p)\log(1-\hat y)\\ \quad\\ &=-\sum^Np\log(\sigma(z))-\sum^N(1-p)\log(1-\sigma(z))\qquad(6) \end{aligned}

식 (6)에서 생각해야 할 것은 확률 pp는 {0,1}\{0,1\}의 값을 갖는다는 것입니다. 주어진 데이터 xx는 반드시 true or false이기 때문이죠. 따라서 식 (6)을 다음처럼 생각할 수 있습니다. zz는 모델이 출력한 logit입니다.

BCE=−∑Nplog⁡(σ(z))−∑N(1−p)log⁡(1−σ(z))=−∑p=1,y=1Nlog⁡(σ(z))−∑p=0,y=−1Nlog⁡(σ(−z))=−∑p=1,y=1Nlog⁡(11+exp⁡(−z))−∑p=0,y=−1Nlog⁡(11+exp⁡(z))=∑p=1,y=1Nlog⁡(1+exp⁡(−z))+∑p=0,y=−1Nlog⁡(1+exp⁡(z))=∑Nlog⁡(1+exp⁡(−yz))=−∑Nlog⁡(11+exp⁡(−yz))=−∑Nlog⁡σ(yz)=∑Nζ(−yz)(7)\begin{aligned} BCE&=-\sum^Np\log(\sigma(z))-\sum^N(1-p)\log(1-\sigma(z))\\ \quad\\ &=-\sum^N_{p=1, y=1}\log(\sigma(z))-\sum^N_{p=0, y=-1}\log(\sigma(-z))\\ \quad\\ &=-\sum^N_{p=1, y=1}\log\left({1\over1+\exp(-z)}\right)-\sum^N_{p=0, y=-1}\log\left({1\over1+\exp(z)}\right)\\ \quad\\ &=\sum^N_{p=1, y=1}\log(1+\exp(-z))+\sum^N_{p=0, y=-1}\log(1+\exp(z))\\ \quad\\ &=\sum^N\log(1+\exp(-yz))=-\sum^N\log\left({1\over1+\exp(-yz)}\right)\\ \quad\\ &=-\sum^N\log\sigma(yz)=\sum^N\zeta(-yz)\qquad(7) \end{aligned}

따라서 positive label을 target으로 본다는 가정 하에, softplus를 BCE loss 대신 사용할 수 있습니다.

참고문헌

  1. PyTorch - Softplus
  2. 생새우초밥집 - Softplus 함수란?
  3. ML_MJSHIN - Activation Functions
  4. PyTorch (runebook.dev) - Softplus
  5. Deepest Documentation - Activation Functions
  6. Analyzing Knowledge Graph Embedding Methods from a Multi-Embedding Interaction Perspective, Hung et al.
profile
Ethan
재미있게 살고 싶은 대학원생
이전 포스트

[최적화이론] 라그랑주 승수법 (Lagrange Multiplier Method)

0개의 댓글