본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 언제든지 댓글 남겨주세요.
Leaky Integrate and Fire (LIF)
Leaky Integrate and Fire(LIF) 모델은 뉴런의 작동 방식을 흉내내기 위해 뉴런이 가지는 다양한 특성들 중에서 핵심적인 몇 가지를 채용했습니다.
- pre neuron들의 spike를 종합(integrate)
- membrane potential이 threshold voltage를 넘으면 spike를 생성하고 voltage 초기화
- membrane potential voltage는 지속적으로 누수(leak)
즉, LIF는 뉴런의 membrane potential의 움직임을 모사한 모델입니다. neurotransmitter 등의 복잡한 부가 요소 없이 직관적이고 단순하기 때문에 연산량도 적습니다. 그래서 가장 기본적인 모델로 많이 사용합니다.
RC회로와의 연관성
LIF는 RC회로와 유사하게 다룰 수 있습니다.
Spike Integrate
pre neuron의 spike들을 입력(전원)으로 취급합니다. 즉, 입력된 spike로 인해 membrane potential이 변화하는 것을 정상상태응답으로 보는 것입니다.
Membrane Potential
membrane potential은 (leakage가 있긴 하지만) spike에 반응하여 전위가 올라갑니다. 즉, 전원의 입력을 받아 전하를 저장하는 커패시터와 동일하게 다룰 수 있습니다.
Voltage Leakage
membrane potential은 지속적인 누수를 통해 resting voltage로 돌아갑니다. 즉, 저항이 존재한다고 할 수 있습니다. 또, voltage leakage는 커패시터에서 전하가 방출되면서 생기는 고유응답으로 볼 수 있습니다.
Threshold Voltage
threshold를 넘으면 spike를 생성하는 메커니즘은 코딩으로 쉽게 구현할 수 있습니다. spike를 생성한 뒤에는 resting voltage로 돌아가는 코드도 만들어주어야 합니다.
LIF 회로 모델링하기
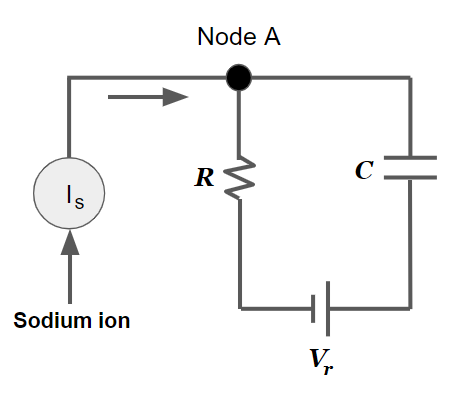
LIF 회로는 위와 같이 생겼습니다. 회로를 from scratch로 코딩하는 것보다는 모델링 함수를 구하고 이를 구현하는 게 빠르고 정확합니다. 오일러 방법을 사용해서 LIF 회로의 시간응답을 구해보겠습니다.
오일러 방법 Euler Method
일 때,
로 근사할 수 있습니다.
먼저 구하려는 LIF의 membrane potential 이고, 이를 모델링한 함수 로 놓을 수 있습니다.
KCL법칙에 의해서,
RC회로에서 시간응답을 구했던 방법으로 계속 식을 전개하면 아래와 같이 정리됩니다.
전압은 전위차를 의미하므로, 휴지전위를 고려하여 가 아니라 가 됩니다.
식(1)을 에 대해 전개하면 다음과 같습니다.
로 놓으면,
이상의 과정을 통해 LIF의 membrane potential을 모델링할 수 있게 되었습니다. 하지만 LIF 구현으로 넘어가기 전에 한 가지 살펴볼 것이 있습니다.
, 즉 (커패시터 용량) X (저항)이었죠? 커패시터 용량이 크거나 저항이 클 수록 같은 일을 위해 더 많은 전류가 필요하다는 점을 기억해둡시다.
식 (2)를 보면 값이 클 수록 변화량이 작아집니다. 따라서 값이 클 수록 membrane potential이 더 느리게 반응합니다. 즉, 값을 통해 뉴런의 반응 빈도를 제어할 수 있습니다. LIF 모델에서는 를 시간 상수(time constant)라고 합니다.
LIF 구현
코드에서 필요한 변수들은 다음과 같습니다.
- membrane potential
- resting voltage
- reset voltage
- 저항(=leakage)
- 입력 전류(=input voltage)
- time constant
먼저 각 변수들을 초기화합니다.
class LIF:
def __init__(self, threshold=-55, v_rest=-65, v_reset=-70, resist=10, tau=10):
self.v_reset = v_reset # reset potential, mV
self.v_rest = v_rest # resting potential, mV
self.R = resist # resistance, nS(나노지멘스)
self.threshold = threshold # threshold potential, mV
self.tau = tau # tau
self.membrane = self.v_reset # 현재 membrane potential, mVthreshold, v_rest, v_reset 값은 실제 뉴런 값을 빌려옵니다. resist는 저항의 역수인 컨덕턴스 값입니다.
이어서 spike를 생성하는 함수를 구현합니다.
def spike(self, input_vt=0, dt=0.001):
"""
dt(delta t) = 1ms (0.001s)
input_vt : input voltage
"""
is_spike = False
self.membrane += (-(self.membrane - self.v_rest) + self.R * input_vt) * dt / self.tau
if self.membrane >= self.threshold:
is_spike = True
self.membrane = self.v_reset
spike_record = {
"spike": is_spike,
"membrane": self.membrane
}
return spike_record마지막으로 LIF 뉴런을 직접 만들어서 자극을 흘렸을 때 반응을 보겠습니다.
if __name__=="__main__":
observe_ms = 100 # ms, 0.1초동안 관찰
neuron1 = LIF() # 뉴런 생성
membrane_potential_history = [] # 0.1초동안의 membrane potential을 기록
dt_history = [i for i in range(observe_ms)] # 시간(ms)
for ms in range(observe_ms):
infos = neuron1.spike(input_vt = 500, dt = 0.001)
membrane_potential_history.append(infos["membrane"])
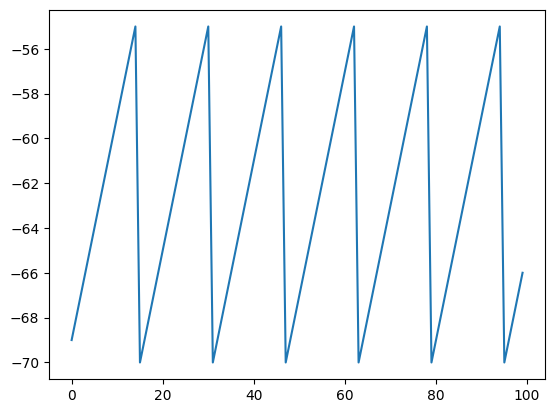
plt.plot(dt_history, membrane_potential_history)
plt.show()결과는 아래와 같습니다.

값을 조정해서 뉴런의 반응 속도를 늦춰보겠습니다.

일 때는 위와 같습니다. 반대로 일 경우 아래와 같이 뉴런의 반응 속도가 더 빨라지는 것을 볼 수 있습니다.
참고문헌
