본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 언제든지 댓글 남겨주세요.
RC회로
RC회로는 저항(R)과 케퍼시터(C)로 이루어진 회로를 말합니다. 저항(R)과 인덕터(=코일, L)로만 이루어진 RL 회로와 같이 1차 회로에 속합니다. 전기를 저장하는 요소가 1개뿐이기 때문에 1차회로라고 부릅니다.
우리는 RC회로의 시간에 따른 전압을 구하는 것이 목표입니다. 왜냐하면 SNN에서 가장 기초가 되는 Leaky Integrate and Fire(LIF) 모델이 RC회로를 기본으로 하기 때문입니다.
뉴런이 신호를 전달하는 과정에서 membrane potential이 매우 중요한 역할이었던 것을 기억하시나요? 그리고 membrane potential은 뉴런 내외부의 전위차(전압)에 따라 변화하죠. 즉, RC회로에서 시간에 따른 전압을 모델링한다는 것은 곧 LIF에서 시간에 따른 membrane potential을 모델링하는 것과 같은 의미입니다.
시간응답
시간응답이란 어떤 시스템의 입출력을 시간에 대한 함수로 표현한 것입니다. 즉, RC회로의 시간응답을 찾으면 그게 바로 우리가 찾는 "시간에 따른 회로 내부 전압의 모델링 함수"가 됩니다. 시간응답을 구하는 방법은 다음과 같습니다.
시간응답(완전응답) = 고유응답(과도응답, 자연응답) + 정상상태응답(강제응답)
고유응답이란 회로 자체의 일반적인 성질에 의해 발생하는 응답입니다. 시간이 흐르면서 점점 감소하는 것이 특징입니다. RC회로에서 고유응답을 구분하는 가장 쉬운 방법은 전원부가 연결되었는지를 보는 것입니다. 만약 전원이 없고 커패시터가 전원 역할을 하고 있다면, 이는 고유응답으로 봅니다.
반대로 정상상태응답은 전원부가 연결되었을 때를 말합니다. 만약 전원도 연결돼 있고 커패시터같은 전력 공급 요소도 붙어 있다면 정상상태응답과 고유응답을 모두 고려해야 합니다.
고유응답 구하기
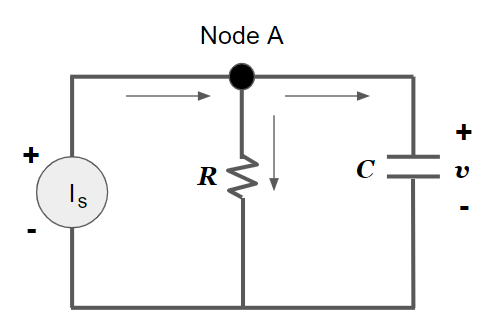
위 그림에서 Node A 기준으로 들어오는 전류와 나가는 전류의 크기는 동일합니다.
만약 전원부가 없는 RC회로라고 가정하면,
커패시터의 특징을 고려하면 는 다음과 같이 표현할 수 있습니다. 여기서 는 커패시터의 용량입니다.
은 옴의 법칙에 따라 다음과 같습니다.
따라서 식 (1)은 다시 아래와 같이 쓸 수 있습니다.
변수분리법을 사용하여 위 식을 정리하면 다음과 같습니다. 는 적분상수입니다.
이 때, 이면 가 됩니다. 즉, 위 RC회로의 초기 전압 입니다.
결과적으로 회로에 흐르는 전압 를 시간 에 따라 모델링할 수 있게 됩니다.
정상상태응답 구하기

고유응답과 마찬가지로 아래와 같은 식을 세울 수 있습니다. 는 연결된 전원부의 전압이고, 는 해당 전원의 용량입니다.
연결된 전원은 DC(직류)이므로 전압이 바뀌지 않으므로, 상수취급하여 식(2)를 아래와 같이 바꿔 쓸 수 있습니다.
상수를 시간에 대해 미분하면 0이므로,
시간응답(완전응답) 구하기
(시간응답)=(고유응답)+(정상상태응답) 이므로,
을 대입하면 식 (3)을 아래와 같이 정리할 수 있습니다.
따라서 값은 아래와 같습니다.
이를 다시 식(3)에 대입하면 회로의 시간응답 함수를 구할 수 있습니다.
참고문헌
