[딥러닝] Consistent Learner

Ethan·2023년 6월 1일

딥러닝 이론

목록 보기

4/6

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 꼭 댓글 남겨주세요.

딥러닝의 목적

딥러닝의 목적은 기본적으로 어떤 것을 추론하는 것입니다. 이 때 추론의 대상은 대부분 어떠한 값, 함수, 또는 범위 등이 됩니다. 가중치를 추정하고, 이를 통해 함수를 근사하는 등의 과정을 생각하면 이해하기 쉽습니다.

학습에 쓸 데이터는 한정돼 있기 때문에, 학습시킨 모델이 다른 데이터에서도 잘 작동하도록 generalization 성능을 확보해야 합니다. 물론 직접 test set을 구축하거나 Cross validation 등의 empirical한 기법을 사용하면 generality를 어느 정도 검증할 수 있습니다. 하지만 이런 과정은 비용이 들어갑니다. 빅 모델이면 인퍼런스 비용조차 부담스러울 수도 있겠죠.

혹시 설계 단계부터 모델의 generality를 확인할 수 있는 방법은 없을까요?

Consistency of the model

다음과 같이 N개의 데이터 세트 $X$ 를 입력 받는 모델 $\hat f_N$ 을 생각해 보겠습니다. $\hat f_N$ 은 estimator function입니다.

\hat f_N(x_1, x_2, \cdots x_N)

이 때 $\hat f_N$ 은 최소한 다음과 같은 조건을 만족해야 합니다.

\hat f_N(x_1, x_2, \cdots x_N)\underset{N\rightarrow\infty}\longrightarrow f_{true}\qquad(1)

식 (1)은 무한한 데이터가 주어진다면 실함수를 찾아낼 수 있다는 의미입니다. 그런데 이 식을 곰곰이 생각해보면 두 가지 의문점이 생깁니다.

$f_{true}$ 를 어떻게 알 수 있을까요?

데이터가 무한하지 않으면 어떻게 될까요?

먼저 1번에 대한 답은 '알 수 없다' 입니다. 당연하죠? $f_{true}$ 를 알 수 있다면 그냥 그 함수를 쓰면 되니까요. 따라서 우리는 $\hat f$ 를 통해 $f_{true}$ 를 근사할 수 밖에 없습니다.

2번에 대한 답 역시 당연하게도, 우리는 절대 무한한 데이터를 가질 수 없습니다. 그래서 주어진 데이터를 가지고 실함수를 근사한 결과에는 필연적으로 오차가 발생합니다.

따라서 우리는 모델의 일관적인 학습 능력(consistency)에 대한 검증이 필요합니다. 데이터를 많이 투입할수록 실함수를 더욱 정확하게 근사할 수 있고, 결과적으로 모델의 성능이 일관적으로 증가할 것이라는 보증이 필요한 것이죠. consistency가 확보되면 자연스럽게 모델의 generality도 확보되기 때문입니다.

Empirical Error (Risk)

일반적으로 모델을 평가할 때는 loss function을 사용합니다. 예를 들어, N개의 데이터 $D=\{x_i, y_i\}^N_{i=1}$ 에 대해 Least Square를 사용하여 모델을 평가한다면, loss function $L_N$ 은 다음과 같이 나타낼 수 있습니다.

L_N(x_1,\cdots,x_N;\theta)={1\over N}\sum_{i=1}^N(\hat y(x_i;\theta)-y_i)^2

이 때, 임의의 $\theta$ 를 파라미터로 하는 실함수의 loss function $L(\theta)$ 에 대해 다음 식이 성립한다는 것을 보이면 $\hat f\rightarrow f_{true}$ 를 증명할 수 있습니다.

L_N(x_1,\cdots,x_N;\theta)\underset{N\rightarrow\infty}\longrightarrow L(\theta)=E_{p(x, y)}[(\hat y(x;\theta)-y)^2]\qquad (2)

식 (2)를 Empirical Error 또는 Empirical Risk라고 합니다.

그런데 $p(x, y)$ 는 우리가 실제로 알 수 없는 실함수이기 때문에 기댓값을 계산할 수 없습니다. 그래서 altering objective를 세우고 이를 만족시키는 방법을 사용합니다.

즉, 우리가 실제로 하고 싶은 것은

\argmin_\theta L(\theta)

를 만족하는 $\theta^*$ 를 찾는 것인데, 이는 불가능하므로

\argmin_\theta L_N(x_1,\cdots,x_N;\theta)

를 만족하는 $\theta'$ 를 대신 찾고

L_N\underset{N\rightarrow\infty}\longrightarrow L\qquad \forall \theta\qquad (3)

를 증명하여 모델의 타당성을 검증하는 것입니다.

Pathological Cases

사실 식 (3)은 사실 주어진 모델이 consistent learner일 필요조건입니다. 왜냐하면 데이터는 무한하지 않기 때문이죠. 그래서 실제로 모델이 consistent learner가 되려면 한 가지 조건이 더 필요합니다.

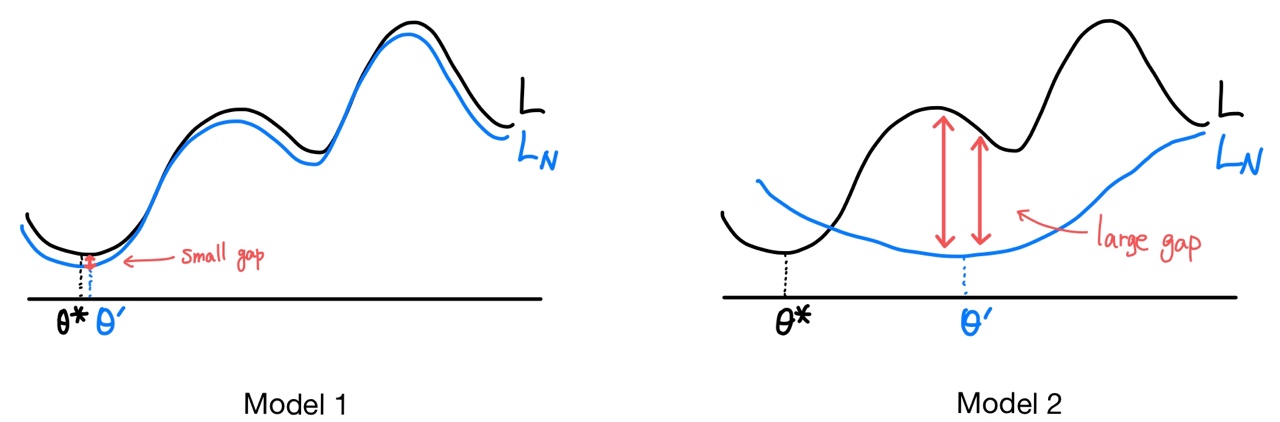
예를 들어 위 그림처럼 $L_N\underset{N\rightarrow\infty}\longrightarrow L$ 이 성립하는 모델 2개를 생각해봅시다.

Model 1은 모든 데이터 포인트에서 true error $L$ 과 model error $L_N$ 간의 차이가 크지 않습니다. 반대로 Model 2는 각각의 데이터 포인트마다 $L$ 과 $L_N$ 의 차이가 들쭉날쭉합니다. 특히 Model 2는 각각의 최적점인 $\theta^*$ 와 $\theta'$ 주변에서 에러의 차이가 매우 크게 나타납니다.

만약 $\theta'$ 까지만 데이터가 주어진다고 해도 Model 1은 별 차이가 없겠지만, Model 2는 오차가 줄어들다가 급격히 커지는 형태가 될 것입니다. 이런 모델을 얼마나 믿을 수 있을까요? 현실적으로 $L_N$ 이 $L$ 로 수렴하려면 데이터가 얼마나 더 필요한지도 모르는 상황에서 데이터를 계속해서 투입할 수 있을까요?

Uniform Convergence

그래서 Uniform Convergence (균등 수렴) 개념을 차용하여 추가적인 조건을 붙입니다. 즉, 모델 $\hat f$ 가 Consistent Learner가 되려면 식 (3)뿐만 아니라 다음 조건도 만족해야 합니다.

P(\sup_\theta(L_N(x_1,\cdots,x_N)-L)>\epsilon)\underset{N\rightarrow\infty}\longrightarrow 0\qquad (4)

임의의 $\theta$ 에 대해 거의 모든 데이터 포인트에서의 오차가 $\epsilon$ 보다 작거나 같아야 한다는 뜻입니다. 데이터 수에 상관없이 실함수와 최대한 비슷하게 근사되어야 한다는 것이죠. 예를 들면 위 그림에서 Model 1과 같은 형태가 되어야 합니다.

Consistent Learner

$L_N\underset{N\rightarrow\infty}\longrightarrow L\qquad \forall \theta$

$P(\sup_\theta(L_N(x_1,\cdots,x_N)-L)>\epsilon)\underset{N\rightarrow\infty}\longrightarrow 0$

위 두가지 조건을 만족하는 모델을 Consistent Learner 라고 합니다. consistent learning이 가능한 모델은 데이터만 충분하다면 지속적으로 성능이 향상되며, 현존하는 대부분의 딥러닝 모델이 이러한 특징을 가지고 있습니다. 대표적인 예시가 바로 transformer입니다.

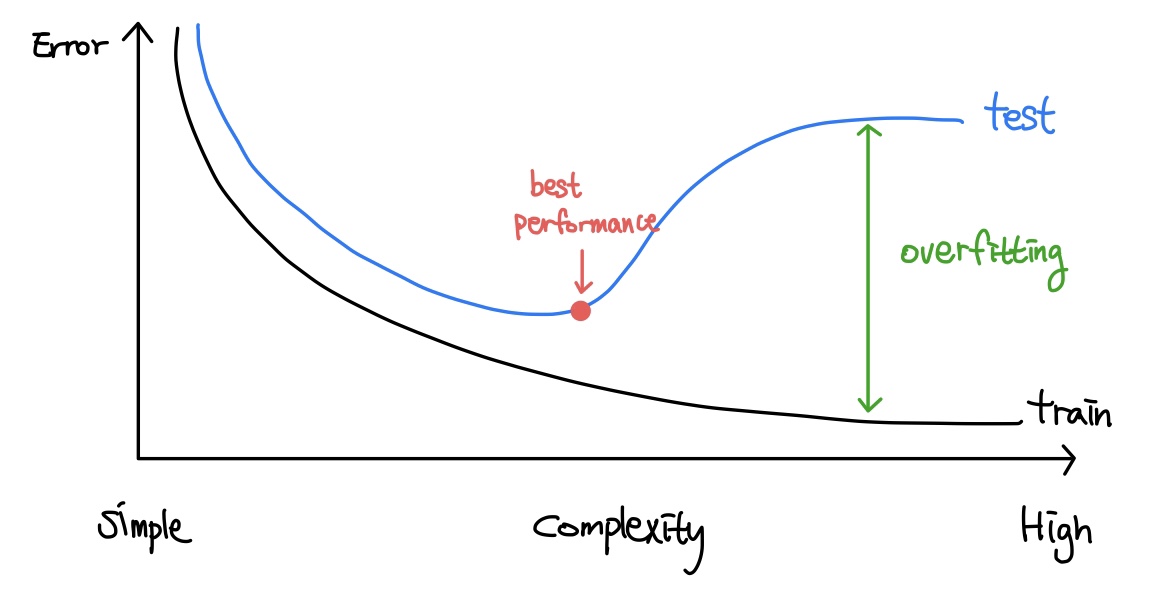
위 그림은 전형적인 Consistent Learner의 learning curve입니다. bias-variance trade off에 의해 복잡한 모델일수록 실함수를 더 잘 근사할 수 있지만, 모델의 complexity가 증가함에 따라 데이터를 추가적으로 투입하지 않으면 overfitting이 발생합니다. 반대로, 모델이 복잡하더라도 충분한 데이터를 투입하면 error rate를 낮추고 generality를 확보할 수 있습니다.

Consistent Learner 모델은 일반적으로 약간의 overfitting이 발생하는 지점이 최적의 성능으로 평가되며, 이런 지점을 찾기 위해 Early Stopping 등의 기법을 사용합니다.

Dominated Convergence Theorem

사실 앞서 살펴본 Consistent Learner의 2가지 조건을 매번 증명하는 것은 번거로운 일입니다. 그래서 Dominated Convergence Theorem(DCT)를 이용합니다. DCT를 한글로는 지배수렴정리라고 합니다.

극한의 적분과 적분의 극한

DCT가 말하는 것은 다음과 같습니다.

\int\lim_{N\rightarrow\infty}f_N\operatorname{d}\theta=\lim_{N\rightarrow\infty}\int f_N\operatorname{d}\theta\qquad (5)\\ \quad\\ \text{if}\quad f_N\rightarrow f\quad \text{and}\quad\exists\quad g(\cdot)\quad \text{s.t.}\quad|f(\theta)|\leq g(\theta)\quad\forall\ x\quad\&\quad\int g(\theta)d\theta < \infty\qquad(6)

즉, $f_N\rightarrow f$ 이고 적분 가능한 함수 $g(\cdot)$ 에 대해 $|f(\theta)|\leq g(\theta)$ , 즉 거의 모든 데이터 포인트 $x$ 에서 $f_N$ 이 수렴하면 $f_N$ 을 적분한 것의 극한과 $f_N$ 의 극한을 적분한 것은 같다는 것입니다.

그런데 식 (6)의 조건은 식(3)과 식(4)를 모두 내포하고 있습니다. 그래서 식 (5)를 보일 수 있다면 주어진 모델이 Consistent Learner라는 뜻이 됩니다.

이게 중요한 이유는 식 (5)의 우변, 즉 우리가 만든 모델을 바로 적분하는 것이 어렵기 때문입니다. 하지만 좌변에 해당하는 부분인 $\int\lim_{N\rightarrow\infty}f_N\operatorname{d}\theta$ 는 조건에 의해 $\int f d\theta$ 가 되므로 계산하기 쉽습니다.