[신호처리] 푸리에 변환의 직관적 이해

Ethan·2024년 8월 30일

Time Series 푸리에 변환

딥러닝 이론

목록 보기

7/7

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 댓글을 남겨주세요.

푸리에 변환

기본 개념

푸리에 변환은 입력받은 신호를 여러 주파수 성분들의 합으로 변환해주는 방법입니다.

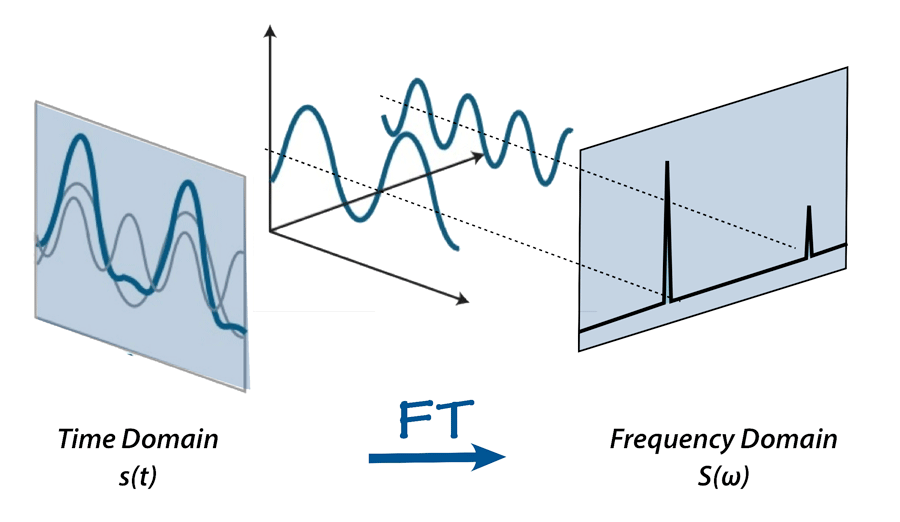
푸리에 변환을 이용하면 위 그림처럼 시간/공간에 대한 함수를 여러 개의 주파수에 대한 함수들로 분해할 수 있습니다.

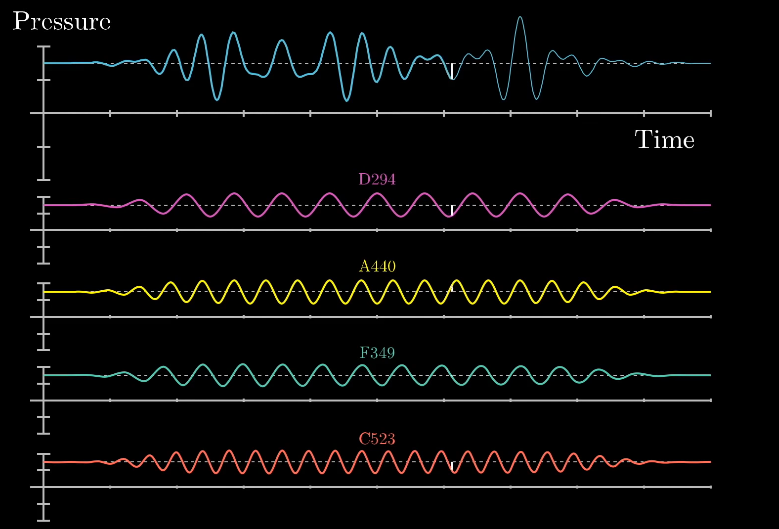
또, 이렇게 구한 함수들을 개별적으로 다시 시간/공간에 대한 함수로 돌려놓을 수도 있습니다. 그러면 위 그림처럼 여러 신호 데이터로 분해되겠죠. 이걸 푸리에 역변환이라고 부릅니다.

데이터를 굳이 주파수 도메인으로 변환하는 이유는 원본 데이터를 시간 도메인에서 바로 처리하기 어렵기 때문입니다. 예를 들어 A, B, C 3명이 대화한 내용을 기록한 녹음파일에서 A의 목소리만 분리하고 싶은 경우를 생각해볼 수 있습니다.

이처럼 원본 데이터를 직접적으로 처리하기 어려울 때 푸리에 변환을 이용해 하위 주파수 성분들로 분해하면 훨씬 다루기 쉬워집니다.

직관적으로 이해하기

푸리에 변환을 수식으로 나타내면 다음과 같습니다.

함수 $h:\mathbb{R}\rightarrow\mathbb{C}$ 에 대해 $\hat{h}=F[h]:\mathbb{R}\rightarrow\mathbb{C}$ 라는 함수가 있을 때,

\hat{h}(t)=F[h](t)=\int^\infty_{-\infty}e^{-2\pi itx}h(x)dx\quad(i=\sqrt{-1})\qquad(1)

여기서 $h$ 는 입력 신호이고 $\hat{h}=F[h]$ 는 푸리에 변환입니다. 위 식은 $h$ 를 임의의 $e^{-2\pi itx}$ 들의 합으로 나타낼 수 있다는 뜻입니다. 그렇다면 $e^{-2\pi itx}$ 는 도대체 무슨 의미일까요?

오일러 공식 Euler's formula

$e^{-2\pi itx}$ 에서 $i$ 는 허수이고 $x,t$ 는 실수입니다. 따라서 실수부와 허수부를 나눠서 보기 위해 오일러 공식을 이용합니다. 오일러 공식은 다음과 같이 삼각함수를 이용해서 복소수 지수를 표현합니다.

e^{i\varphi}=\cos \varphi+i\sin \varphi\qquad(2)

복소평면 상에 단위원을 그려보면 오일러 공식의 의미를 조금 더 이해할 수 있는데요.

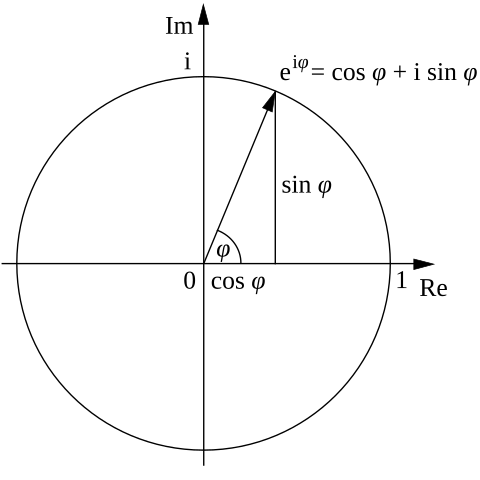
즉, $e^{i\varphi}$ 는 단위원 위에서 $\varphi\ \text{rad}$ 만큼 이동한 점을 나타내는 벡터입니다.

이제 이 특성을 이용해서 시간 $t$ 에 따라 단위원 위를 회전하는 점 $p$ 가 있다고 가정해 보겠습니다. 그러면 점 $p$ 의 위치를 다음과 같이 표현할 수 있습니다.

p=e^{-2\pi itx}=\cos 2\pi tx-i\sin 2\pi tx

여기서 $2\pi\ (\text{rad})$ 는 단위원의 둘레의 길이입니다. 따라서 $p$ 가 원 위를 $n$ 바퀴 돌려면 $tx$ 의 값이 정수여야 합니다. 그런데 $t$ 는 '점 $p$ 가 이동한 시간'이고 거리=속력x시간이니까 $x$ 는 '점 $p$ 가 단위원 위를 이동하는 속도'가 됩니다. (물론 속도!=속력이지만 직관적인 이해를 위해...)

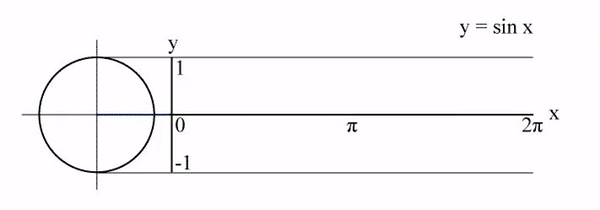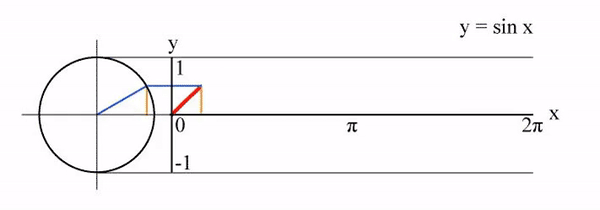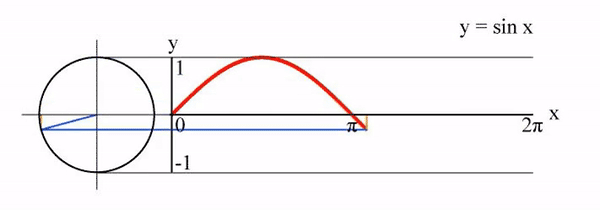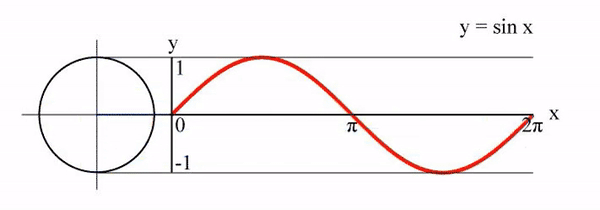
그리고 원 위를 회전하는 점 $p$ 의 움직임은 위 그림처럼 주기함수로 표현할 수 있습니다. 따라서 $x$ 는 그래프의 진동수 = 주파수가 됩니다. 결과적으로 푸리에 변환을 통해 원본 신호를 $x$ 값에 따라 다양한 주파수를 갖는 주기함수들로 분해할 수 있습니다.