[최적화이론] 헤세 행렬 Hessian Metrix

Ethan·2023년 4월 15일
Hessian최적화이론헤시안
2

최적화이론

목록 보기
1/5

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용이나 오류가 있다면 언제든지 댓글 남겨주세요.

헤세 행렬 Hessian Metrix

헤세 행렬이란 주어진 함수 f={x1,x2,⋯ ,xn}f=\{x_1,x_2,\cdots,x_n\}에 대해 2계 도함수들을 모아놓은 행렬입니다. 헤시안 행렬이라고도 부릅니다. 다음과 같이 나타낼 수 있습니다.

H(f)=[∂2f∂x12∂2f∂x1x2⋯∂2f∂x1xn∂2f∂x2x1∂2f∂x22⋯⋮⋮⋮⋱⋮∂2f∂xnx1⋯⋯∂2f∂xn2](1)H(f)= \begin{bmatrix} \partial^2 f\over\partial x_1^2 & \partial^2f\over\partial x_1x_2& \cdots & \partial^2f\over\partial x_1x_n \\ \partial^2f\over\partial x_2x_1 & \partial^2f\over\partial x_2^2 & \cdots & \vdots \\ \vdots & \vdots & \ddots & \vdots\\ \partial^2f\over\partial x_nx_1 & \cdots & \cdots& \partial^2f\over\partial x_n^2 \end{bmatrix}\qquad(1)

2차 미분의 의미

헤세 행렬이 갖는 의미를 이해하기 위해 먼저 미분이란 무엇인지 생각해 봅시다.

미분은 변화율에 관한 서술입니다. 따라서 2차 미분은 변화율의 변화율에 관한 서술이라고 할 수 있습니다. 그리고 어떤 함수의 1차 미분은 기울기입니다. 그렇다면 기울기의 변화율은 무엇일까요?

정답은 곡률입니다. 즉, 헤세 행렬의 의미는 주어진 점에 대해 함수의 기울기가 각각의 방향으로 어떻게 변하는가를 나타낸 것입니다.

직관적인 이해를 위해 다음과 같은 함수를 가정해 보겠습니다.

y=12ax2+bx+c(2)y = {1\over2}ax^2+bx+c\qquad(2)

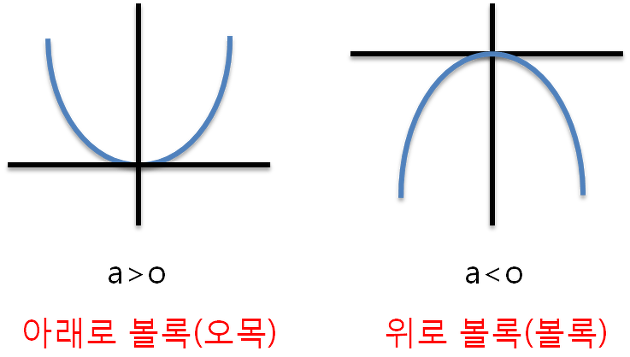
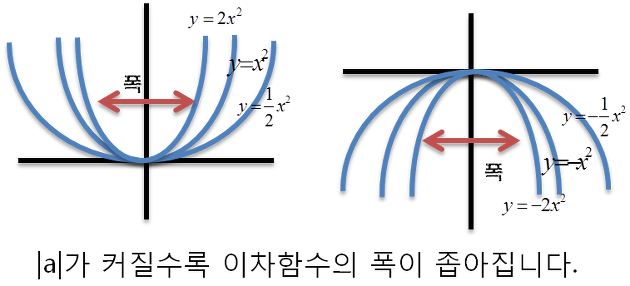
식 (2)의 이계도함수는 aa입니다. 만약 a>0a>0이라면 위 그림과 같이 convex한 형태가 됩니다. 2차 미분값은 곡률이므로, aa 값이 클 수록 당연히 더 가파른 형태가 됩니다. 따라서 해당 함수의 폭이 더 좁아지겠죠?

그리고 이는 헤세 행렬에도 마찬가지로 적용됩니다. 예컨대 식 (1)에서 ∂2f∂x12\partial^2f\over\partial x_1^2는 변수 x1x_1에 대한 함수 ff의 곡률을 의미합니다. ∂2f∂x1x2\partial^2f\over\partial x_1x_2는 변수 x1,x2x_1, x_2에 대한 함수 ff의 곡률이 되겠죠.

어떠한 변수에 대한 함수의 곡률이라는 단어가 직관적으로 와 닿지 않을 수 있습니다. 조금 더 쉬운 이해를 위해 모든 행렬은 선형변환이라는 점을 생각해 보겠습니다. 예를 들어 헤세 행렬은 다음과 같이 주어진 함수를 볼록하거나 오목하게 만드는 선형변환입니다.

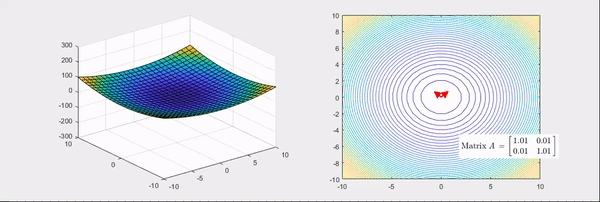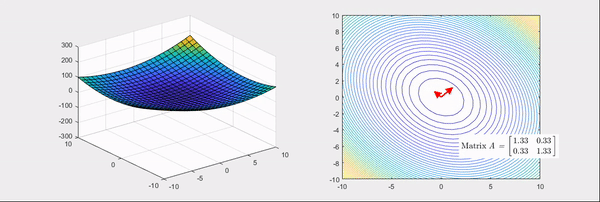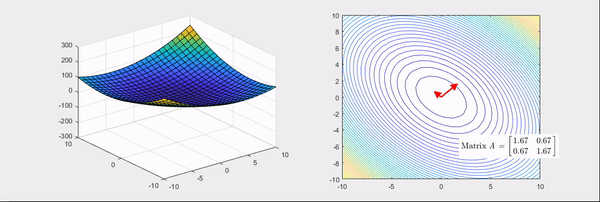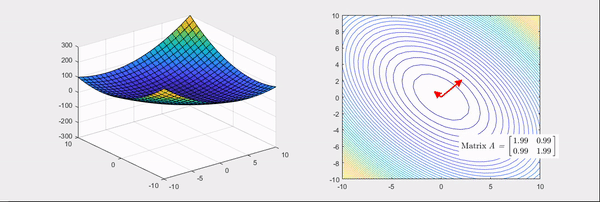
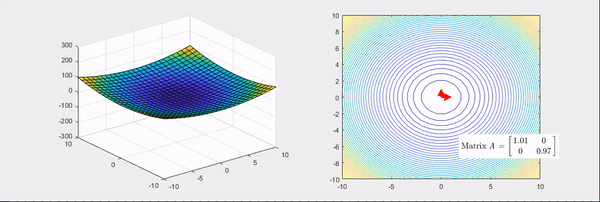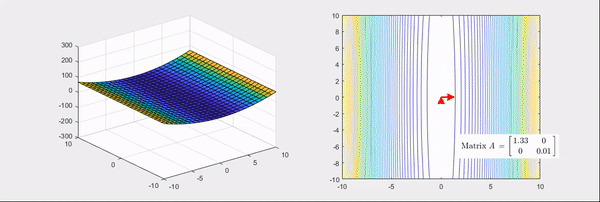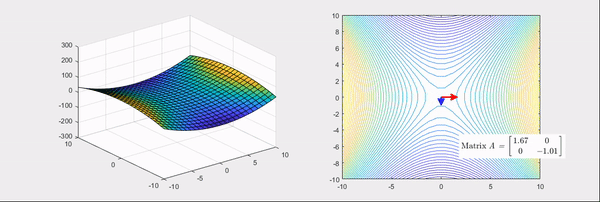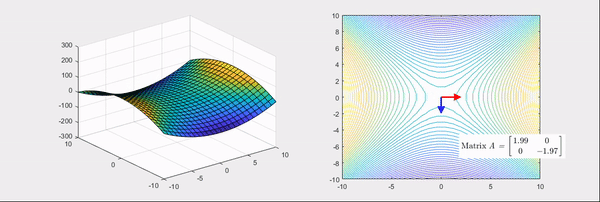
즉, ∂2f∂x12,∂2f∂x1x2{\partial^2f\over\partial x_1^2}, {\partial^2f\over\partial x_1x_2}은 각각 x1x_1 방향과 x1,x2x_1, x_2 방향으로 ff의 기울기가 어떻게 변하는가를 나타낸 값입니다. 값이 크면 해당 방향으로 더 급격하게 기울어지고, 값이 음수면 해당 방향과 반대로 기울어진다는 뜻입니다.

이 점을 통해 알 수 있는 헤세 행렬의 중요한 특징이 있는데, 바로 ff의 이계도함수가 연속이라면 H(f)H(f)는 대칭이라는 것입니다. 즉, ∂2f∂x1x2=∂2f∂x2x1{\partial^2f\over\partial x_1x_2}={\partial^2f\over\partial x_2x_1}이 성립합니다. 따라서 헤세 행렬은 항상 대칭행렬입니다.

헤세 행렬의 활용

헤세 행렬을 통해 주어진 점에 대해 모든 방향의 기울기 정보를 알 수 있으므로, 해당 함수의 convex 여부를 분석할 수 있습니다. 예를 들어 다음과 같은 함수를 가정해 보겠습니다.

f(x,y,z)=(x−y)2+2z2f(x, y, z) = (x-y)^2+2z^2

이 함수의 헤세 행렬은 다음과 같습니다.

H(f)=[2−20−220004](3)H(f)= \begin{bmatrix} 2 & -2 & 0 \\ -2 & 2 & 0 \\ 0 & 0 & 4 \\ \end{bmatrix}\qquad(3)

식 (3)의 고유값을 구하면 다음과 같습니다.

(2−λ)(2−λ)(4−λ)−((−2−λ)(−2−λ)(4−λ))=0λ=4,0(2-\lambda)(2-\lambda)(4-\lambda)-((-2-\lambda)(-2-\lambda)(4-\lambda))=0\\ \quad\\ \lambda = 4, 0

즉, H(f)H(f)는 positive semi definite 입니다. 다시 말해 함수 ff의 모든 임계점에 대해 모든 방향에서 그래디언트의 방향이 바뀌지 않으므로, ff는 convex function입니다. strictly convex는 아니라는 점을 주의합시다.

물론 주어진 함수 f(x,y,z)=A2+B2f(x,y,z)=A^2+B^2 꼴임을 보고 바로 convex 형태임을 알 수도 있습니다.

참고문헌

  1. 공돌이의 수학정리노트 - 헤세 행렬(Hessian Matrix)의 기하학적 의미
  2. 테일러 급수, 헤시안 행렬
  3. Worldpad - 헤세 행렬의 의미
  4. 다크프로그래머 - Gradient, Jacobian 행렬, Hessian 행렬, Laplacian
  5. Ch4. Numerical Computation for Deep Learning+
  6. 그림 출처
profile
Ethan
재미있게 살고 싶은 대학원생
다음 포스트

[최적화이론] 최대 우도 추정 Maximum Likelihood Estimation (MLE)

0개의 댓글