[추천시스템] Variational Autoencoders for Collaborative Filtering (MultVAE)

Ethan·2023년 7월 15일

Papers Review

목록 보기

10/18

본 블로그의 모든 글은 직접 공부하고 남기는 기록입니다.
잘못된 내용/오류 지적이나 추가 의견은 댓글로 남겨주시면 감사하겠습니다.

Published: WWW, 2018
Paper: https://dl.acm.org/doi/abs/10.1145/3178876.3186150

[요약]

Collaborative Filtering에 VAE를 적용
Decoder에서 베르누이 분포 대신 multinomial 분포를 활용
- user의 각 item에 대한 interaction을 multinomial로 모델링

[서론]

Abstract

Collaborative Filitering에 Variational AutoEncoder (VAE)를 활용한 논문입니다. Basic VAE와 달리 decoder에서 prior로 multinomial 분포를 가정합니다. 이하 논문에서 제안한 모델을 MultVAE라고 지칭합니다.

사용하는 분포 이외에 기존 VAE에서 크게 달라진 점은 없습니다.

1. Introduction

기존의 Latent Factor (LF) 모델들은 본질적으로 linear합니다. (이에 대해서는 여기의 설명을 참고)

그래서 VAE를 활용한 Collaborative Filtering을 제안합니다. 특히 prior distribution으로 multinomial 분포를 채택했는데, 추천 분야에서 흔히 사용하는 ranking 기반 loss를 모델링하는데 gaussian이나 logistic 분포보다 더 적합하기 때문이라고 합니다.

basic VAE가 over-regularized 됐다고도 주장하는데, 이 부분에 대해서는 후술합니다.

[본론]

2. Method

Notations

iten index $i \in \{1, ..., I\}$ , user index $u \in \{1, ..., U\}$
user-item matrix (binarized click rate) $X \in \mathbb{N}^{U\times I}$
$x_u=[x_{u1}, x_{u2}, ... x_{uI}]^T \in \mathbb{N}^I$ 형태의 bag of words vector

2.1 Model

각 user $u$ 에 대해 $K$ 개의 차원을 가진 latent representation $z_u \sim \mathcal{N}(0, I_K)$ 를 gaussian 분포에서 샘플링하는 것부터 시작합니다. 여기까지는 basic VAE와 동일합니다.

이후 디코더에 해당하는 MLP layer $f_\theta\in\mathbb{R}^I$ 를 $z_u$ 를 변환한 값에 softmax를 취해 normalization을 진행합니다. 이렇게 얻은 벡터 $\pi(z_u)$ 는 전체 item에 대한 각 user의 선호 확률로 해석할 수 있습니다. 이상의 과정을 순서대로 수식으로 표현하면 다음과 같습니다.

\begin{aligned} x_u\rightarrow z_u\sim\mathcal{N}(0,I_K)\qquad&\cdots\qquad\text{encoding}\\ \quad\\ \pi(z_u)\propto \exp(f_\theta(z_u))\qquad&\cdots\qquad\text{normalization}\\ \quad\\ x_u\sim\text{Mult}(N_u, \pi(z_u))\qquad&\cdots\qquad\text{reconstruction} \end{aligned}

결과적으로 latent factor 관점에서 user $u$ 의 log-likelihood는 다음과 같이 표현할 수 있습니다.

\log p_\theta(x_u|z_u)\overset{c}{=}\sum_i x_{ui}\log \pi_i(z_u)

위 식의 좌변과 우변은 거의 같습니다 $(\overset{c}{=})$ . 우변을 보면 $\log \pi(z_u)$ 를 통해 non-zero $x_u$ 에 대해 probability mass를 분배하지만, $\pi(z_u)$ 의 합이 1이어야 하기 때문에 모델이 상대적으로 더 높은 가능성을 가진 item에 더 많은 비중을 주게 됩니다. 쉽게 말해서 user가 선호할 확률이 높은 item일수록 더 높은 확률값을 주게 되어 Top-N ranking loss를 통해 잘 최적화된다는 의미입니다.

2.2 Variational inference

MultVAE도 basic VAE처럼 Variational Inference를 이용하여 파라미터 $\theta$ 를 추정합니다. 논문에서는 prior distribution $q(z_u)$ 를 다음과 같이 factorized gaussian distribution으로 설정합니다.

q(z_u)=\mathcal{N}(\mu_u, \text{diag}\{\sigma^2_u\})

결과적으로 모델의 학습 목표는 $KL(q(z_u)||p_\theta(z_u|x_u))$ 를 최소화하기 위해 $\{\mu_u, \sigma^2_u\}$ 를 최적화하는 것이 됩니다.

2.2.1 Amortized inference and the variational autoencoder

user / item 수가 늘어날수록 $\{\mu_u, \sigma_u^2\}$ 를 최적화하기 위한 파라미터 수도 증가하기 때문에 성능적 병목 현상이 발생할 수 있습니다. (user-item 조합 1개당 $\mu,\sigma$ 하나씩을 계산해야 하므로)

그래서 개별 파라미터를 일일히 계산하는 대신 다음과 같이 $\mu_\phi(x_u), \sigma_\phi(x_u)$ 벡터들로 표현되는 data-dependent function $g_\phi$ 를 사용합니다. 이 때 $g_\phi$ 를 흔히 inference model이라고 부릅니다. data-dependent function이라는 말에서 어렴풋이 느껴지듯이, 이게 바로 MultVAE의 인코더입니다.

g_\phi(x_u)\equiv[\mu_\phi(x_u), \sigma_\phi(x_u)]\in\mathbb{R}^{2K}

결과적으로 우리가 찾는 variational distribution $q_\phi(z_u|x_u)$ 는 다음과 같이 나타낼 수 있습니다.

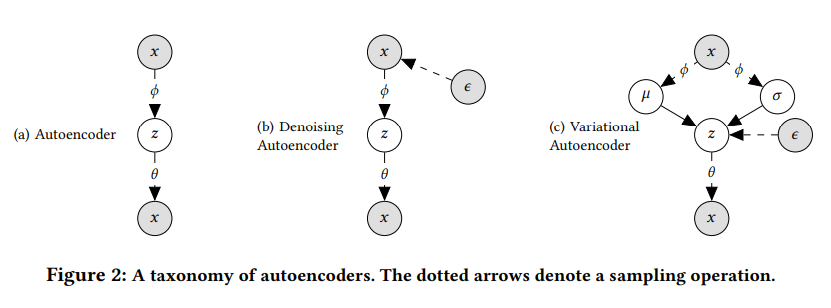
q_\phi(z_u|x_u)=\mathcal{N}(\mu_\phi(x_u), \text{diag}\{\sigma^2_\phi(x_u)\})

즉, $x_u$ 라는 데이터를 입력하면 inference model이 variational distribution $q_\phi(z_u|x_u)$ 를 계산하며, 이 분포를 최적화하면 posterior 분포 $p(z_u|x_u)$ 를 근사한 것과 같습니다. 위 그림의 (c)와 같은 구조로 계산이 진행되는 것이죠.

Learning VAEs

VAE 계열에서 사용하는 variational inference는 다음과 같은 ELBO를 갖습니다.

\log p(x_u;\theta)\geq E_{q_\phi(z_u|x_u)}[\log p_\theta(x_u|z_u)]-KL(q_\phi(z_u|x_u)||p(z_u))\equiv \mathcal{L}(x_u;\theta,\phi)

당연히 basic VAE와 동일한 문제가 발생합니다. 우변의 KL Divergence를 최소화할 때, $z_u$ 를 $q_\phi$ 에서 sampling해서 파라미터를 추정하면 되는데 sampling 연산은 미분이 안 되죠? 그래서 reparameterization trick을 사용합니다.

\epsilon\sim\mathcal{N}(0,I_K),\qquad z_u=\mu_\phi(x_u)+\epsilon\odot\sigma_\phi(x_u)

이상의 과정을 알고리즘으로 표현하면 다음과 같습니다.

2.2.2 Alternative interpretation of ELBO

\begin{aligned} E_{q_\phi(z_u|x_u)}[\log p_\theta(x_u|z_u)]\qquad&\cdots\qquad\text{(negative) reconstruction error}\\ \quad\\ KL(q_\phi(z_u|x_u)||p(z_u))\qquad&\cdots\qquad\text{regularization} \end{aligned}

사실 본 논문에서 ELBO를 바라보는 관점은 위와 같습니다. 그래서 아래와 같이 regularization을 제어하기 위한 파라미터 $\beta$ 를 도입하죠.

E_{q_\phi(z_u|x_u)}[\log p_\theta(x_u|z_u)]-\beta \cdot KL(q_\phi(z_u|x_u)||p(z_u))

이 때 $\beta\neq1$ 로 둡니다. 즉, 더 이상 log likelihood를 기준으로 ELBO를 최적화하지 않습니다. $\beta<1$ 로 설정하면 constraint ${1\over U}\sum_uq(z|x_u)\approx p(z)=\mathcal{N}(z;0,I_K)$ 의 영향력이 줄어드는데, 이 과정에서 ancestral sampling을 통한 user history 생성 능력이 저하되는 문제가 발생합니다.

이미지나 언어 모델이라면 이러한 부분이 큰 문제가 될 수 있습니다. 하지만 추천 생성 모델의 목표는 좋은 추천을 생성하는 것이라는 점을 기억해야 합니다. log likelihood를 최대화하는 건 우리의 본질적인 목표가 아닙니다. 즉, $\beta$ 를 설정한다고 해서 결과적으로 우리가 손해볼 것은 하나도 없다는 것이죠.

이러한 관점에서 VAE 계열을 비롯한 생성 모델이 좋은 성능을 보이는 이유는 implicit feedback에 존재하는 variance에 어느 정도 유연하게 대처가 가능하기 때문이라고 생각할 수 있습니다.

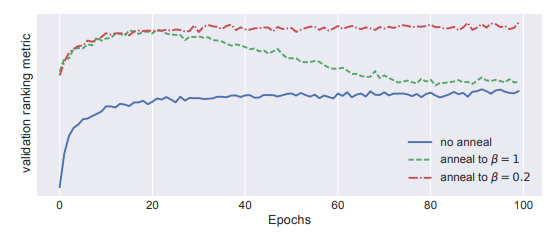
위 그림은 $\beta$ 값을 0부터 1까지 조금씩 늘려가며 annealing을 진행한 결과입니다. 논문에서 언급한 대로, $\beta$ 를 적당히 설정하는 것이 오히려 성능 향상을 이끌어내고 있습니다.

2.3 A taxonomy of autoencoders

일반적인 AE 모델에서 MLE를 하는 경우를 생각해보겠습니다. 식으로는 다음과 같이 나타낼 수 있습니다.

\begin{aligned} \theta^{AE}, \phi^{AE}&=\argmax_{\theta, \phi}\sum_uE_{\delta(z_u-g_\phi(x_u))}[\log p_\theta(x_u|z_u)]\qquad(1)\\ \quad\\ &=\argmax_{\theta, \phi}\sum_u\log p_\theta(x_u|g_\phi(x_u))\qquad(2) \end{aligned}

AE와 DAE는 delta variational distribution $q_\phi(z_u|x_u)=\delta(z_u-g_\phi(x_u))$ 을 사용하여 (1)번 항을 쉽게 최적화할 수 있습니다. 쉽게 말하면 생성 데이터와 원본의 차이를 줄이는 식으로 학습한다는 뜻입니다. 그래서 VAE처럼 posterior $q_\phi(z_u|x_u)$ 를 임의의 prior에 맞출 필요가 없습니다. 대신 non zero $x_u$ 에만 확률을 분배하기 때문에 overfitting의 가능성이 높아진다는 문제가 있습니다. DAE 계열의 모델들은 input layer에 dropout을 걸어서 이런 문제를 완화했습니다.

2.4 Prediction

기본적으로 MultVAE나 MultDAE나 추론 과정은 동일합니다. user history data $x$ 가 주어지면, 정규화하지 않은 multinomial probability $f_\theta(z)$ 를 통해 전체 item의 ranking을 매깁니다. MultVAE의 경우 variational distribution의 평균값 $\mu_\phi(x)$ 을 latent representation $z$ 로 사용하고, MultDAE의 경우 $g_\phi(x)$ 를 그대로 $z$ 로 사용합니다.

DAE 계열은 파라미터를 하나만 생성하고, VAE 계열은 평균과 분산 2개를 생성하기 때문에 후자의 computational cost가 높을 수밖에 없습니다. 실무에서 빠른 inference가 필요하다면 DAE 계열을 사용하는 것이 더 좋을 수 있습니다. DAE 계열이 하이퍼파라미터 설정에 조금 더 민감하지만 두 모델의 성능 차이가 그리 큰 편은 아닙니다.

VAEs on sparse data

연구에 따르면 VAE 계열 모델들은 large, sparse, high-dimensional data에서 underfitting 되는 경향을 보인다고 합니다. 위에서 본 annealing 실험 결과에서도 동일한 현상이 나타나는데, $\beta\leq1$ 로 설정하여 ancestral sampling 능력을 조금 포기하는 대신 user의 interaction data에 기반하여 생성을 수행합니다. 쉽게 말해서 추천 분야의 데이터가 워낙 sparse하기 때문에 베이지안적인 접근이 더 적절하다는 의미입니다.

4. Empirical study & Else...

실험 데이터셋으로는 MovieLens-20M, Netflix Prize, Million Song Dataset을 사용했습니다. 몇 가지 실험 데이터와 결과에 대해 설명하는데 2023년도 기준으로 대부분의 데이터와 baseline은 outdated 된 편입니다. 자세한 내용이 궁금하신 분은 뒤쪽을 직접 읽어보시는 걸 추천드립니다.

참고문헌

Ethan

재미있게 살고 싶은 대학원생

이전 포스트

[딥러닝] Batch Normalization: Accelerating Deep Network Training by Reducing Internal Covariate Shift