Abstact

• 최근 언어 모델은 대규모 데이터로 사전 학습되는 추세인데, GPT-3 175B와 같은 엄청난 매개변수를 가진 모델을 Full fine-tuning하는 것은 비용이 너무 많이 듬

• 본 논문은 Low-Rank Adaptation을 제안하여 기존 모델의 가중치는 그대로 고정시킨 상태에서, 학습 가능한 rank decomposition matrices를 기존 모델의 특정 계층에 삽입하는 방법으로 Full fine-tuning 대비 학습해야 할 매개변수의 수는 1만배 줄이고, GPU 메모리 사용량은 3배 감소시킬 수 있음

• LoRA는 RoBERTa, DeBERTa, GPT-2, 그리고 GPT-3에서 파인튜닝과 맞먹는 성능을 보이며, 추론 시 추가 지연이 발생하지 않음

1 Introduction

• fune-tuning 할 때 막대한 자원을 먹지 않도록 기존 모델은 그대로 freeze하고, adapter를 별도로 학습하는 방법이 연구되었지만, 추론 속도가 줄어든다던지, 시퀀스 길이를 감소시킨다던지, 기존 튜닝 방법과 비교해서 성능이 떨어진다던지 하는 효율성과 모델 품질 사이의 Trade-off가 발생함

• 연구진은 model adaptation 과정에서 모든 매개변수 차원에서 중요한 정보를 담고 있지 않고, 저차원에서도 충분히 중요한 정보가 담길 수 있다는 것을 포착하여(intrinsic rank), 매개변수를 low-rank 행렬 분해 방식으로 학습하고, 기존 모델 가중치는 freeze

• 예를 들어, GPT-3은 매개변수의 rank가 무려 12,888이지만, LoRA를 통해 rank를 1로 줄여도 충분히 adaptation이 가능하기 때문에 공간-연산 측면에서 효율적

2 Problem Statement

기존 Full fine-tuning

$\max_{\Phi} \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log P_{\Phi}(y_t | x, y_{<t})$

• $(x, y) \in Z$ : 데이터셋 Z 에 포함된 모든 (입력, 정답) 쌍
• t=1 부터 |y| 까지 정답 문장 y의 각 토큰에 대한 확률을 log-likelihood로 최대화
• 각 downstream task마다 여러 개의 파인튜닝 모델을 저장, 배포하기 부담 됨

LoRA

$\max_{\Theta} \sum_{(x,y) \in Z} \sum_{t=1}^{|y|} \log P_{\Phi_0 + \Delta\Phi(\Theta)}(y_t | x, y_{<t}) \quad$

• 본 논문에서는 전체 매개변수 $\Phi$는 freeze하고, 작은 행렬 $\Theta$(기존 파라미터 수의 0.01%)를 사용하여 $\Delta\Phi$를 저차원으로 표현

4 Our Method

4.1 LOW-RANK-PARAMETRIZED UPDATE MATRICES

• 특정 task에 맞춰 model adaptation을 할 때, 가중치를 작은 공간으로 projection해도 효율적인 학습이 가능하다는 것을 가정하여 사전 훈련 가중치 행렬 $W_0 \in \mathbb{R}^{d \times k}$를 업데이트 하기 위한 Low-Rank decompostion을 통해 아래와 같이 표현

$W_0 + \Delta W = W_0 + BA$

• 여기서 $B \in \mathbb{R}^{d \times r} , A \in \mathbb{R}^{r \times k}$ 이며, 랭크 r 은 $\min(d,k)$ 보다 훨씬 작음

• 기존에는 주어진 입력 벡터 x에 대해 $h = W_0x$ 라 할 때, LoRA는 아래와 같이 표현

$h = W_0x + \Delta Wx = W_0x + BAx$

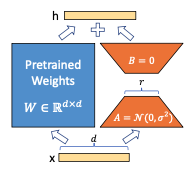
• A는 Random Gaussian initialization를 사용, B는 0으로 모든 가중치를 조정해서 처음 학습할 때는 $\Delta W = BA$ 가 0이 됨
• 이후, $\Delta Wx 를 \frac{\alpha}{r}$ 로 스케일링하는데, $\alpha$를 조정하면 leaning-rate와 같이 학습을 촉진시키며, r값을 변경할 때 하이퍼파라미터 재조정의 번거로움을 줄일 수 있음

4.2 APPLYING LORA TO TRANSFORMER

• Transformer architecture는 self-attention query, key, value, output 가중치 행렬 4개, MLP에 2개의 가중치 행렬이 존재하는데 본 연구는 Attention 가중치만을 조정함

• 추론 지연을 없애기 위해 BA를 기존 가중치에 병합할 수 있지만, 이렇게 되면 다른 작업에 대한 BA를 사용할 수 없기 때문에 LoRA모듈 사용이 어렵다는 단점 존재

5 EMPIRICAL EXPERIMENTS

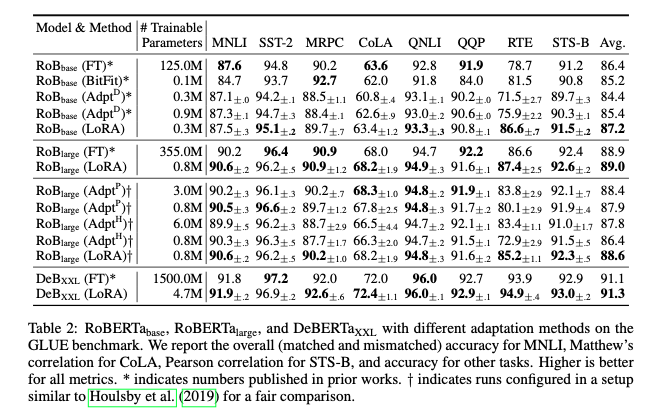
• BERT계열 모델인 RoBERTa, DeBERTa 2모델이 Full fine-tuning과 견주는 성능을 달성

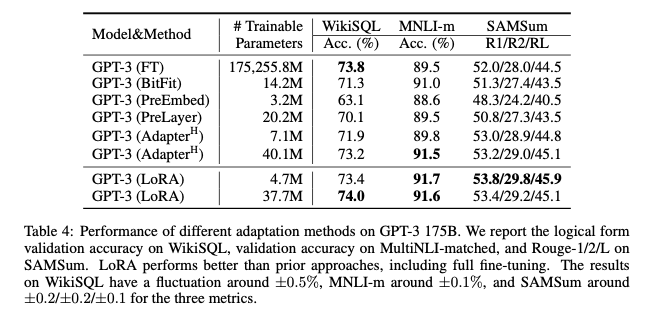
• GPT-3 모델의 경우에도 기존 풀 파인튜닝과 비교해 동등하거나 더 좋은 성능을 기록

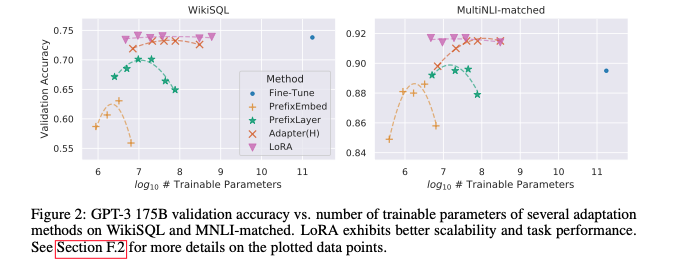
• LoRA는 다른 방법론과 비교해서 일관되게 더 좋은 성능을 달성했고, 파라미터 개수(r 개수)를 늘린다고 해서 성능이 유의미하게 향상되는 것은 아니었음

7 UNDERSTANDING THE LOW-RANK UPDATES

7.1 WHICH WEIGHT MATRICES IN TRANSFORMER SHOULD WE APPLY LORA TO?

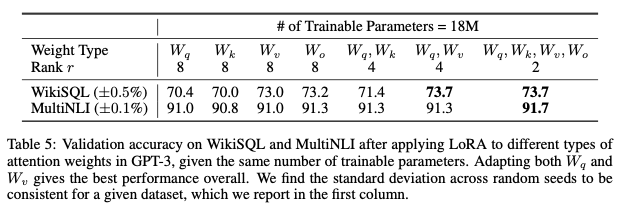
• 학습할 수 있는 추가 가중치가 제한되어있을 때, GPT-3 모델을 기준으로 $W_q$와 $W_v$를 전부 adaptation하는 것이 가장 좋은 성능을 보임

• Rank의 수보다는 여러 가중치를 많이 adaptatio하는 것이 바람직함

7.2 WHAT IS THE OPTIMAL RANK r FOR LORA?

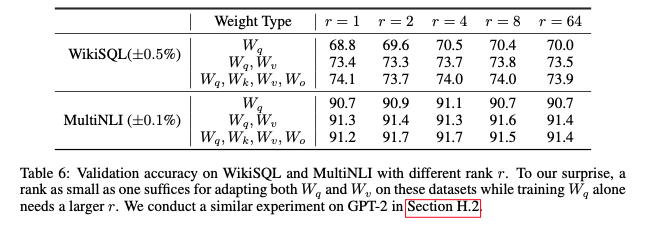
• 단일 가중치를 학습하는 것보다 여러 가중치를 학습하는 게 우수하며, 이는 Update matrix가 intrinsic rank임을 시사함

• but, downstream task가 사전 학습에 사용된 언어와 다르거나, 데이터 구성이 상이하면 전체 모델을 다시 학습하는 것이 작은 r을 사용한 LoRA보다 확실히 더 좋은 성능을 낼 수 있음

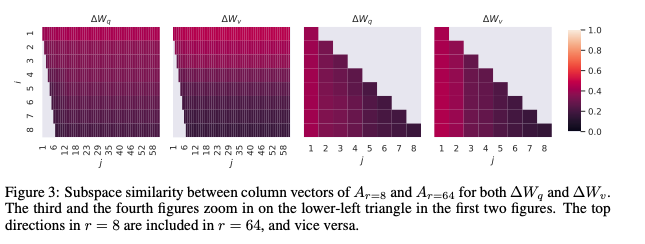
• 동일한 r=8과 r=64 모델을 비교한 결과, r=8 및 r=64 에서 가장 유용한 방향은 최상위 특이벡터들이며, 나머지 방향들은 학습 과정에서 쌓인 노이즈일 가능성이 크기 때문에 adaptation matrix은 실제로 매우 낮은 랭크를 가짐

7.3 HOW DOES THE ADAPTATION MATRIX ∆W COMPARE TO W?

• ∆W는 무작위 행렬과 비교했을 때 W와 더 강한 상관관계를 가지며, 이는 ∆W가 이미 W에 존재하는 일부 특징을 증폭(amplify)하고 있음을 시사한다.

• ∆W는 W의 최상위 특이 방향을 단순히 반복하는 것이 아니라, W에서 강조되지 않은 방향을 증폭시킨다.

8 CONCLUSION AND FUTURE WORK

• LLM을 파인튜닝 하는 것은 매우 비싸고 비효율적이다

• LoRA는 기존 파인튜닝 방법과 비교해서 성능이 비슷하면서도 추론 속도 저하, 시퀀스 길이 감소 문제도 없을 뿐만 아니라, adapter만 갈아끼우면 되기 때문에 신속한 task전환이 가능한 좋은 방법임

• 하지만, 여전히 LoRA의 메커니즘이 뭔지, 휴리스틱한 방법으로 분해할 가중치 행렬을 선택하는 데 명확한 기준이 있을지에 대해서는 여전히 향후 연구 과제가 될 수 있음