영상을 기하학적으로 변환할 때 아무런 정보를 받지 못하는 pixel이 생기게 된다.
이러한 픽셀을 채우는 방식에는 여러가지가 있다.
이번 글에서는 픽셀을 채우는 방식중 하나인 Interpolation에 대해 정리하고 그 중 하나인 Bilinear 방식이 어떻게 동작하는지 설명하겠다.
Interpolation의 종류
- Nearest-neighbour
- Linear
- Cubic
1차원
Nearest-neighbour은 가장 가까운 화소값을 사용하는 방식이다.
Linear은 인접한 2개 화소의 화소값과 거리비를 사용하여 결정하는 방식이다.
Cublic은 인접한 4개 화소의 화소값과 거리에 따른 가중치로 결정하는 방식이다.
Linear는 2차함수, Cublic은 3차 함수로 부터 유도되어진다. (2개의 점은 항상 직선으로 나타낼 수 있지만 3개부터는 직선에 위치시키기 어렵기 때문이다.)
2차원
2차원에서 관점에서 바라보면 Nearest-neighbour은 2D nearest-neighbour이 되고 Linear, Cublic은 각각 Bilinear, Bicublic방식이라 불리게 된다.
또한 축이 하나 더 생겼기 때문에 Bilinear은 4개, Bicublic은 16개의 인접한 화소값으로 부터 유도된다.
Linear interpolation
Linear interpolation을 직관적인 방법으로 설명하겠다.
Interpolation은 아래 그림에서 봤을 때 x1, x2사이의 a라는 점이 있을 때 b를 구하는 방식이다.
그림에서 유도되어진 식은 비례식의 느낌으로 접근하면 이해하기 쉽다.
x1~a와 a~x2의 거리를 d1, d2라고 할때 b의 값은 d1, d2의 거리에 의해 결정된다.
d1, d2의 거리 비율을 식으로 나타내면 d1/(d1 + d2), d2/(d1+d2)으로 나타낼 수 있다.
b는 y1, y2의 값을 d1, d2에 비례하여 받게 된다. b에게 큰 영향을 주는 것은 거리가 가까운 y1이고 멀리 떨어져 있는 y2는 적은 영향을 주게된다.
그렇기 때문에 값이 작은 d1/(d1 + d2)에는 y2를 곱하고 , 값이 큰 d2/(d1+d2)에는 y1을 곱해 더하는 것이 Linear interpolation이다.
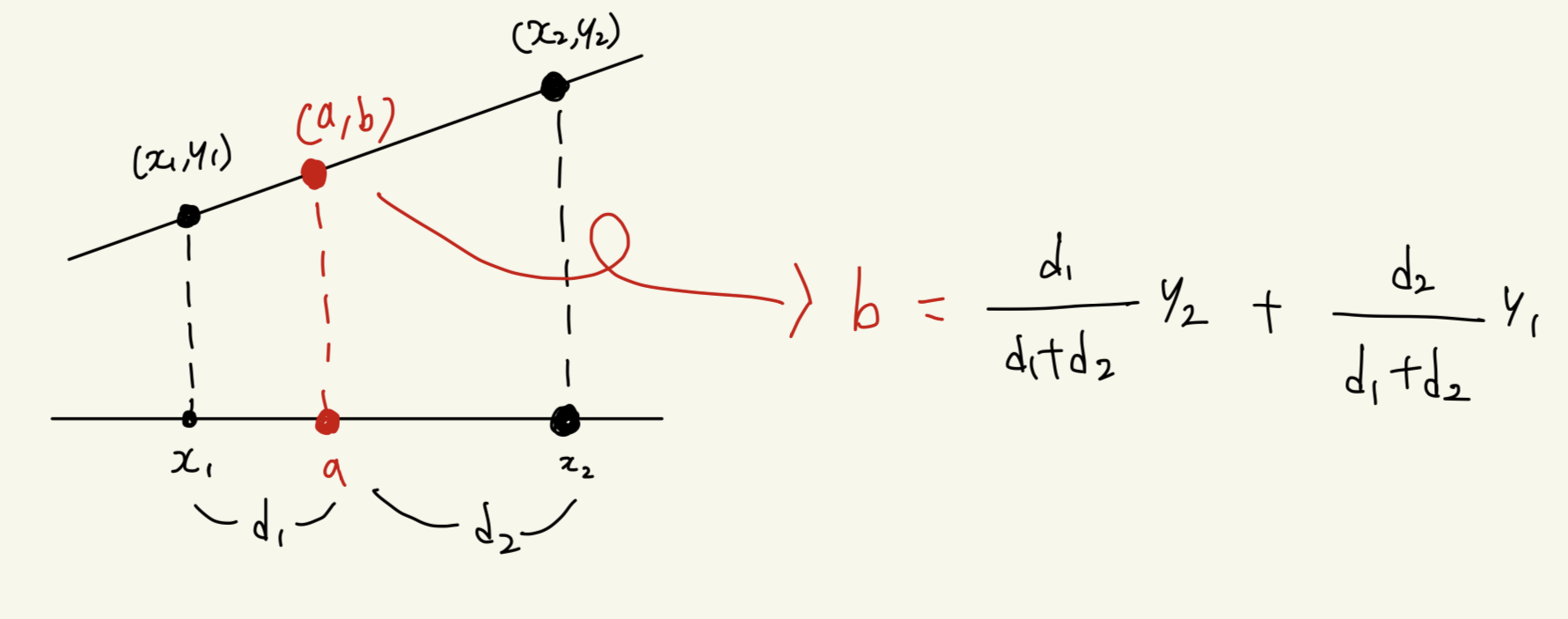
Bilinear Interpolation
Bilinear Interpolation로 2x2 이미지를 4x4 이미지로 만드는 과정은 다음과 같다.
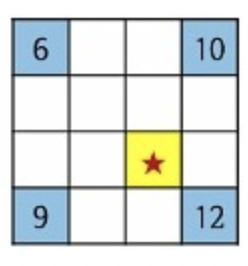
이 그림은 6, 10, 9, 12로 이루어져 있던 2x2이미지를 16x16으로 늘린 것이다. 이미지를 늘리니 그림 처럼 빈칸이 생기게 되는데 이 빈칸들을 Bilinear Interpolation으로 채워야한다.
별이 그려진 빈칸을 채우기 위해선 다음과 같은 순서로 Interpolation을 진행하면 된다.
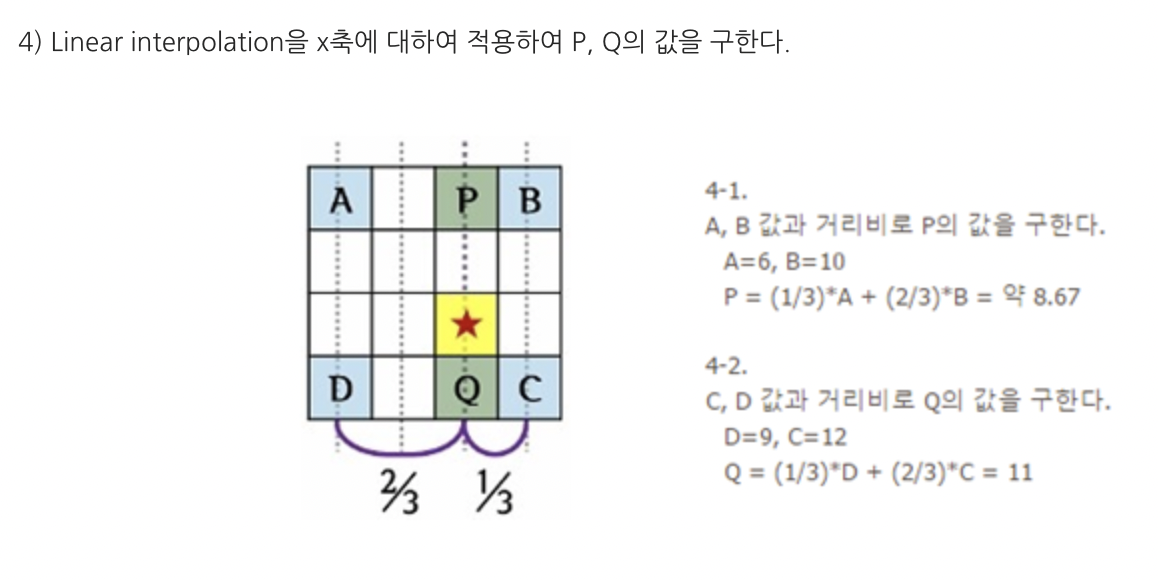
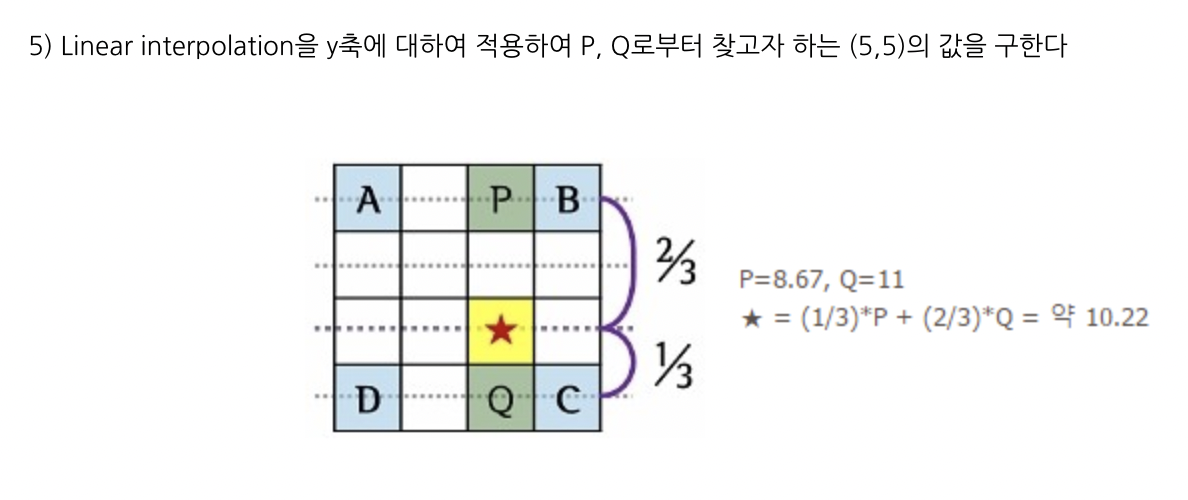
이러한 방법으로 빈칸들을 채워나가면 2x2이미지를 4x4이미지로 만들 수 있다.
[출처]
Bilinear Interpolation 파트는 https://blog.naver.com/aorigin/220947541918 에 있는 자료를 이용하여 작성하였습니다.
