Random Process - Probability Density Function

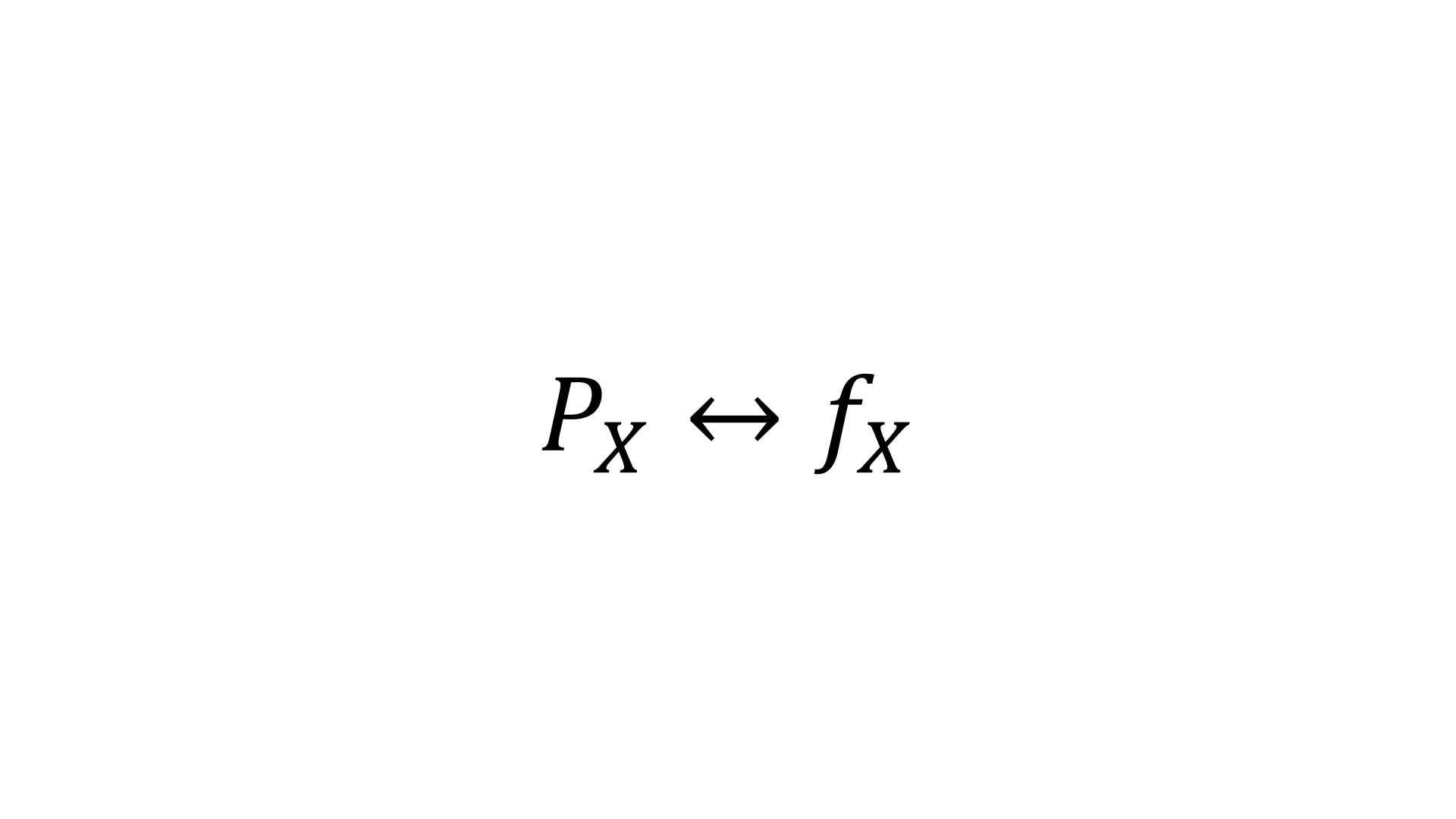
  이 글은 22-2학기 김운경 교수님의 Random Process 강의와 Peyton의 "Probability, Random Variables and Random Signal Principles" 4판을 참고하였음을 밝혀드립니다. 본 글의 'The Fundamental Theorem of Calculus'는 허야용 교수님의 2021년 2학기 해석학 2 lecture note를 참고하였음을 밝혀드립니다.

  저번 글에서는 random variable과 CDF의 여러가지 증명에 대해 살펴보았습니다. 이번 글에서는, CDF와 관련된 probability density function (PDF)에 대해 살펴보고, 이에 대한 증명을 해보고자 합니다.

  PDF의 증명에 앞서, 먼저 the fundamental theorem of calculus에 대해 알아보겠습니다.

The Fundamental Theorem of Calculus I) Let $f$ be a Riemann integrable function on $[a, b]$. Define

Assume that $f$ is continuous at $x_0 \in [a, b]$. Then $F$ is differentiable at $x_0$ and

  이에 대한 증명은 이 글에서 상세하게 다루지는 않겠습니다. 하지만 중요한 것은 interval $[a, b]$와 리만 적분 가능한 함수 $f$가 주어졌을 때, $f$의 리만 적분 함수 $F$가 존재한다면, $F$와 $f$ 사이에 $F'(x_0)=f(x_0)$와 같은 관계식이 성립한다는 사실입니다. 즉, $f$를 알면 $F$를 구할 수 있으며, 반대로 $F$를 알면 $f$를 구할 수 있습니다. 즉, $f$와 $F$는 필요충분 조건을 만족합니다.

FTC가 필요한 이유?

  우리는 먼저 임의의 random variable $X \sim (\mathbb{R}, \mathcal{P}(\mathbb{R}),P_X)$에 대해 CDF $F_X$가 존재한다는 사실을 알고 있습니다. 그렇다면 interval $\mathbb{R}$에 대해 $F_X$에 대해 대응되는 Riemann integrable function $f_X$가 존재한다고 합시다. 그렇다면 다음과 같은 관계가 성립할 것입니다.

$by \, FTC \, I$, ($f_X$가 존재하는 경우);

  그런데 앞서 principle 3는 다음과 같다고 언급한 적이 있습니다.

Principle 3) $\forall A,B \in \mathcal{P}(\mathbb{R}):[A \cap B= \empty]$

  따라서 주어진 임의의 interval $I=[a, b]$에 대해, 다음과 같은 관계식이 만족합니다.

  Connected 되지 않은 무한한 interval에서 정의할 수 있는 르베그 적분과 같은 경우는 이 글에서 다루지 않겠습니다. 하지만 몇 가지 경우, $\mathbb{R}$의 부분집합은 유한한 interval의 합집합으로 나타낼 수 있으며, 그 집합을 $A$라고 하면 $P_X$와 $f_X$ 사이에는 다음과 같은 관계가 성립합니다.

따라서 다음과 같은 관계가 만족한다고 결론내릴 수 있습니다.

  따라서 우리는 $P_X$를 알면 $f_X$를 알고, 그 반대의 경우도 마찬가지입니다. 즉, 주어진 random bariable의 PDF를 알면, 이에 대한 probability space를 안다는 것과 마찬가지라는 사실입니다.

제안된 확률 모델링의 문제점?

  지금까지 확률 공간에 대한 모델링과, 이와 관련된 여러가지 규칙들을 살펴보았습니다. 배운 것들을 돌아보면, 임의의 확률 공간을 모델링하고, 이에 파생되는 새로운 확률 공간을 생성하는 것은 매우 정확한 규칙 아래에서 이루어진다는 사실을 살펴볼 수 있습니다.

  이와 같은 모델링에서 파생될 수 있는 문제점은 무엇일까요? 한 가지 예상할 수 있는 것은, 애초에 모델링 과정에서 사소한 오류가 발생할 경우, 그 이후로 오류를 수정할 수 없다는 사실입니다. 또한 확률 공간의 특성이 변할 경우, 예를 들어 probability measure에 map되는 weight가 팽창하거나 수축할 경우 principle 5를 적용하여 파생된 확률 공간을 생성할 수 없게 됩니다.

Conclusion

  이번 글에서는 확률 공간과 PDF에 대해 살펴보았습니다. 주어진 확률 공간의 PDF를 알면, 특수한 경우 그 확률 공간을 아는 것이나 다름 없습니다. 따라서 확률 변수를 안다는 것은 확률 변수에 대한 PDF를 안다는 것과 동의어이며, 그만큼 PDF를 아는 것이 매우 중요합니다. 다음 글에서는 principle 5를 통해 새로운 확률 공간의 PDF가 생성되는 것에 대해 살펴보고자 합니다. 긴 글 읽어주셔서 감사합니다!