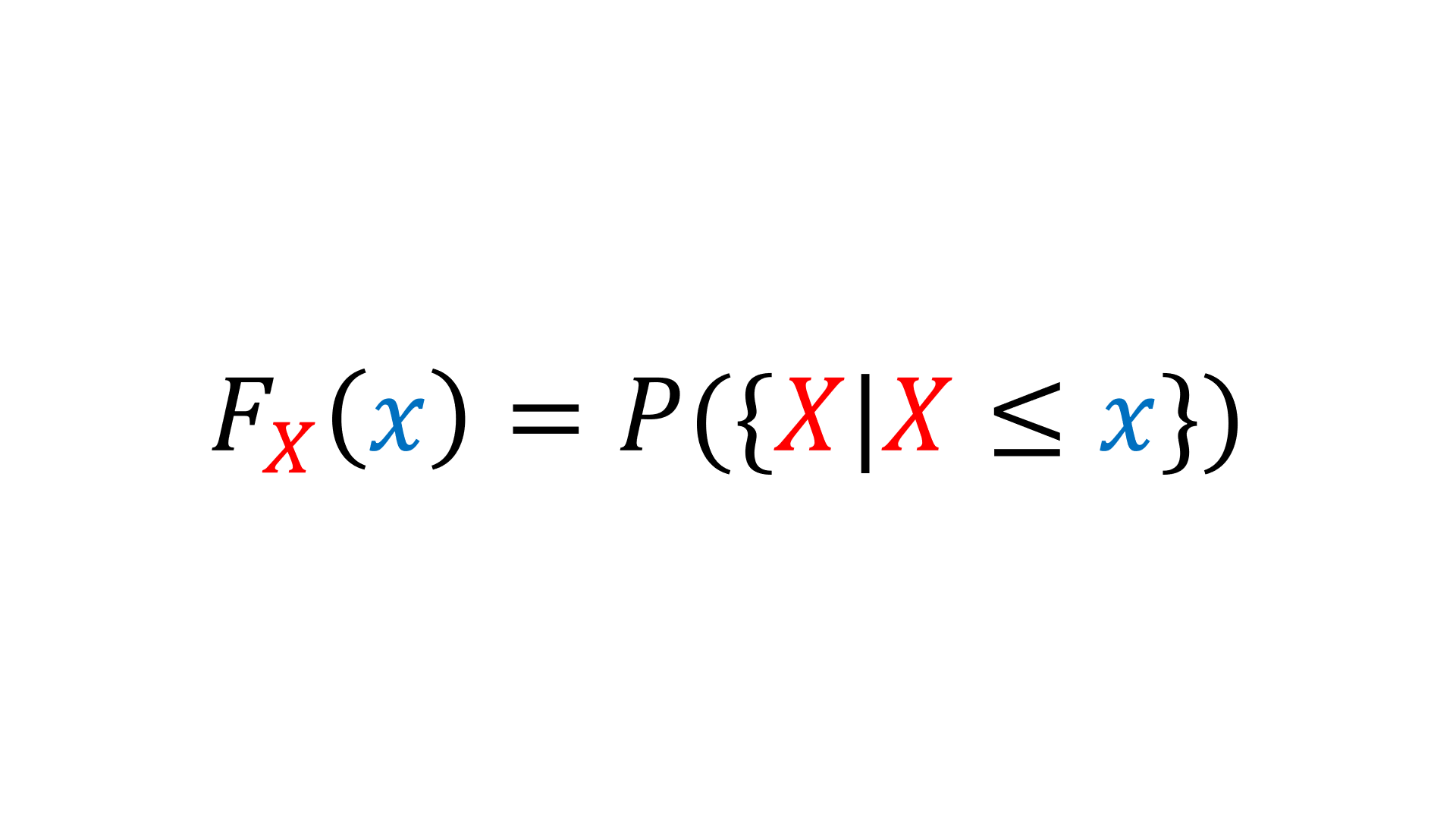Random Process - Random Variable

  저번 글에서는 principle 5에 대해서 다루어보았습니다. 이번 글에서는, random 객체 중 하나인 random variable에 대해 다루어볼까 합니다.

Random variable이란?

  확률 공간 $(\mathbb{R}, \mathcal{P}(\mathbb{R}), P)$으로 정의할 수 있는 random한 객체를 우리는 random variable이라고 합니다. 즉, 어떤 random한 객체의 outcome이 항상 실수의 형태라면, 그 객체는 random variable이라고 할 수 있습니다.

  이 random variable은, 다른 random 객체와는 다르게 cumulative probability distribution function(CDF)이 unique하게 존재합니다. Uniqueness에 대한 증명은 다음에 기회가 되면 다루도록 하겠습니다. 즉 CDF는 특정한 set $A \in \mathcal{P}(\mathbb{R})$들에 대한 probability measure이며 다음과 같이 정의가 가능합니다.

  이러한 distribution function은 다음과 같은 6가지 성질을 만족합니다. 이번 글에서는 이 6가지 성질에 대한 증명을 하고, 글을 마치겠습니다.

(1): $\lim_{x \to -\infty} F_{X}(x)=0$;
(2): $\lim_{x \to \infty} F_{X}(x)=1$;
(3): $0 \le F_{X}(x) \le 1$;
(4): $F_{X}(x_1) \le F_{X}(x_2) \; if \; x_1 < x_2$;
(5): $P(\{x_1 < x \le x_2 \}) = F_X(x_2) - F_X(x_1)$;
(6): $F_X(x^+)=F_X(x)$;

(1): Prove that

Proof)

Lemma: Let $[x_n]_{n \in \mathbb{N}}$ be an arbitrary decreasing sequence with $\lim_{n \to \infty}x_n=-\infty;$ Then $\cap^{\infty}_{n=1}(-\infty, x_n]=\emptyset;$
Proof of lemma)
Let $\cap^{\infty}_{n=1}(-\infty, x_n] \neq \emptyset$ where $\exist x \in \cap^{\infty}_{n=1}(-\infty, x_n];$
Then $\exist k \in \mathbb{N}:x_k < x$ because $x_n \rightarrow -\infty;$
Since $x \not\in (-\infty, x_k]$ for some $k \in \mathbb{N}$, so $x \not\in \cap^{\infty}_{n=1}(-\infty, x_n]$, which contradicts the fact that $x \in \cap^{\infty}_{n=1}(-\infty, x_n];$
Hence $\cap^{\infty}_{n=1}(-\infty, x_n] = \empty;$

Also, we can say that $\cap^{m}_{n=1}(-\infty, x_n] = (-\infty, x_m]$ for any $m \in \mathbb{N};$
So, by Measure of Limit of Increasing Sequence of Measurable Sets:

  Because $[x_n]_{n \in \mathbb{N}}$ was an arbitrary decreasing real sequence, we can conclude that $\lim_{x \to -\infty}F_X(x) = 0 \blacksquare$

(2): Prove that

Proof)

  Let $[x_n]_{n \in \mathbb{N}}$ be an increasing sequence with $\lim_{n \to \infty}x_n=\infty$;
Then:

$\square$

From Measure of Limit of Increasing Sequence of Measurable Sets, $P(\cup^{\infty}_{n=1}(-\infty, x_n]) = \lim_{n \to \infty}P((-\infty, x_n])$.
Thus,

$\square$

Since $[x_n]_{n \in \mathbb{N}}$ was arbitrary,

$\blacksquare$

(3): Prove that

Proof)

We know thtat for any $a \in \mathcal{P}(\mathbb{R})$:

Hence $0 \le P(a) \le 1;$
$\blacksquare$

(4): Prove that

Proof)

Let $A = (-\infty, x_1]$ and $B = (-\infty, x_2]$ where $P(A) = F_X(x_1)$ and $P(B) = F_X(x_2)$;
Then $B \setminus A = (x_1, x_2]$;

Thus:

Hence, $F_X(x_1) \ge F_X(x_2)$
$\blacksquare$

(5): Prove that

Proof)

Let $A = (-\infty, x_1]$ and $B = (-\infty, x_2]$ where $P(A) = F_X(x_1)$ and $P(B) = F_X(x_2)$;
Then $B \setminus A = (x_1, x_2]$ where:

Hence we can conclude that:

$\blacksquare$

(6): Prove that

Proof)

For any $a \in \mathbb{R}$, let $[x_n]_{n \in \mathbb{N}}$ be an arbitrary decreasing sequence where

And we define a set: $A_n = \{ x|x \le x_n \}$ where $A_n \in \mathcal{P}(\mathbb{R});$

Lemma: $\cap^{\infty}_{n=1}A_n = \{x|x \le a \};$

Proof of lemma)
($\Rightarrow$) For $m \in \mathbb{R}$, $\forall \alpha \in A_m$: let $\alpha > a;$
Then $\exists x_k:k > m$ where $\alpha> x_k \ge a$ because $\lim_{n \to \infty}x_n = a;$
Thus we can conclude that $\nexists \alpha \in \cap^{\infty}_{n=1}A_n$ where $\alpha > a;$
Hence we can conclude that $\cap^{\infty}_{n=1}A_n \subset \{x|x \le a \};$

($\Leftarrow$) Let $\alpha \in \{x|x \le a \};$
For each $m \in \mathbb{N} : a \le x_m$;
Hence $\{x|x \le a \} \subset \cap^{\infty}_{n=1}A_n$
$\square$

So, for any decreasing sequence $[x_n]_{n \in \mathbb{N}}$, $\lim_{n \to \infty}x_n=a$:

for any $a \in \mathbb{N};$

Hence we can conclude that $F_X(a^+) = F_X(a), \; \forall a \in \mathbb{R}$
$\blacksquare$

Conclusion

  지금까지 CDF와 그 성질에 대해 살펴보았습니다. CDF는 probability measure을 represent할 수 있는 함수이고, 위에서 증명한 6가지 성질을 만족합니다. 이 중 1, 2, 4 그리고 6번은 주어진 함수가 유효한 distribution function인지 분별하는데 사용되기도 합니다. 다음으로 우리가 할 것은 CDF가 미분 가능하고 그 도함수가 연속일 때(혹은 유한한 곳에서 불연속이고 piecewise continuous 할 때), density function을 구하고, 이 density function은 어떤 성질을 만족하는지에 대해 살펴보겠습니다. 지금까지 긴 글 읽어주셔서 감사합니다!