Random Process - Probability Measure에 관련된 규칙들

이 글은 22-2학기 김운경 교수님의 Random Process 강의와 Peyton의 "Probability, Random Variables and Random Signal Principles" 4판을 참고하였음을 밝혀드립니다.

  저번 글에서는 모르는 객체의 확률을 표현하는 방식인 probability space $(S, \mathcal{P}(S), P)$에 대해 다루었습니다. 이번에는, power set $\mathcal{P}(S)$에 양의 실수값을 mapping하는 함수 probability measure $P$에 대해 이야기해보겠습니다.

  Probability measure $P$는 앞서 정의했던 것처럼 power set $\mathcal{P}(S)$의 원소들의 모든 값들을 양의 실수로 mapping합니다. 따라서 다음과 같은 첫 번째 규칙을 제정할 수 있습니다.

Axiom I. For all $A \in \mathcal{P}(S):P(A) \ge 0$ ;

  두 번째로 필요한 규칙은 확률 값의 상한을 정하는 것입니다. 특정 event에 대한 확률이 상한값을 갖는다는 것은, outcome이 항상 그 event의 원소일 수 밖에 없다는 것과 동일한 의미입니다.

  일단 확실한 것은 모르는 객체의 outcome은 항상 sample space의 원소일 것이라는 사실입니다. 그 상한값을 1이라고 정할 때, 이를 수식으로 표현하면 다음과 같습니다.

Axiom II. $P(S)=1 \leftrightarrow P(s \in S)=1$ ;

  세 번째 규칙은, 나중에 증명 과정에서 왜 필요한지에 대해 더 확실히 드러나기 때문에, 일단 먼저 이에 대해 적어놓겠습니다.

Axiom III. $\forall A, B \in \mathcal{P}(S) : [A \cap B = \emptyset]$ ;

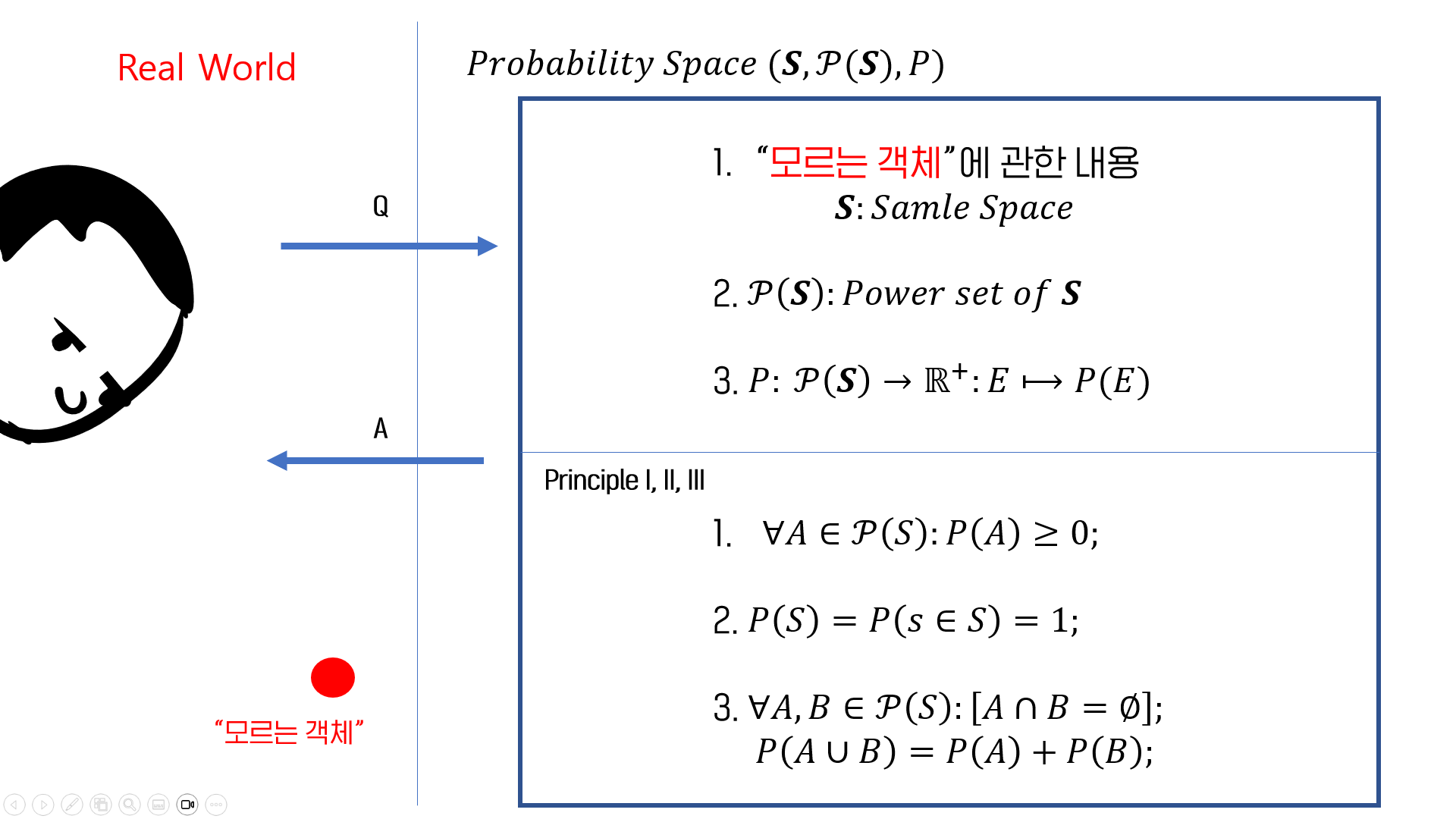
  지금까지 probability space에 대한 정의를 했고, probability measure의 세 가지 규칙에 대해 다루었습니다. 왜 이런 정의와 규칙이 필요한 것일까요? 다음 그림을 보면 이해가 편합니다.

Why Probability Space?

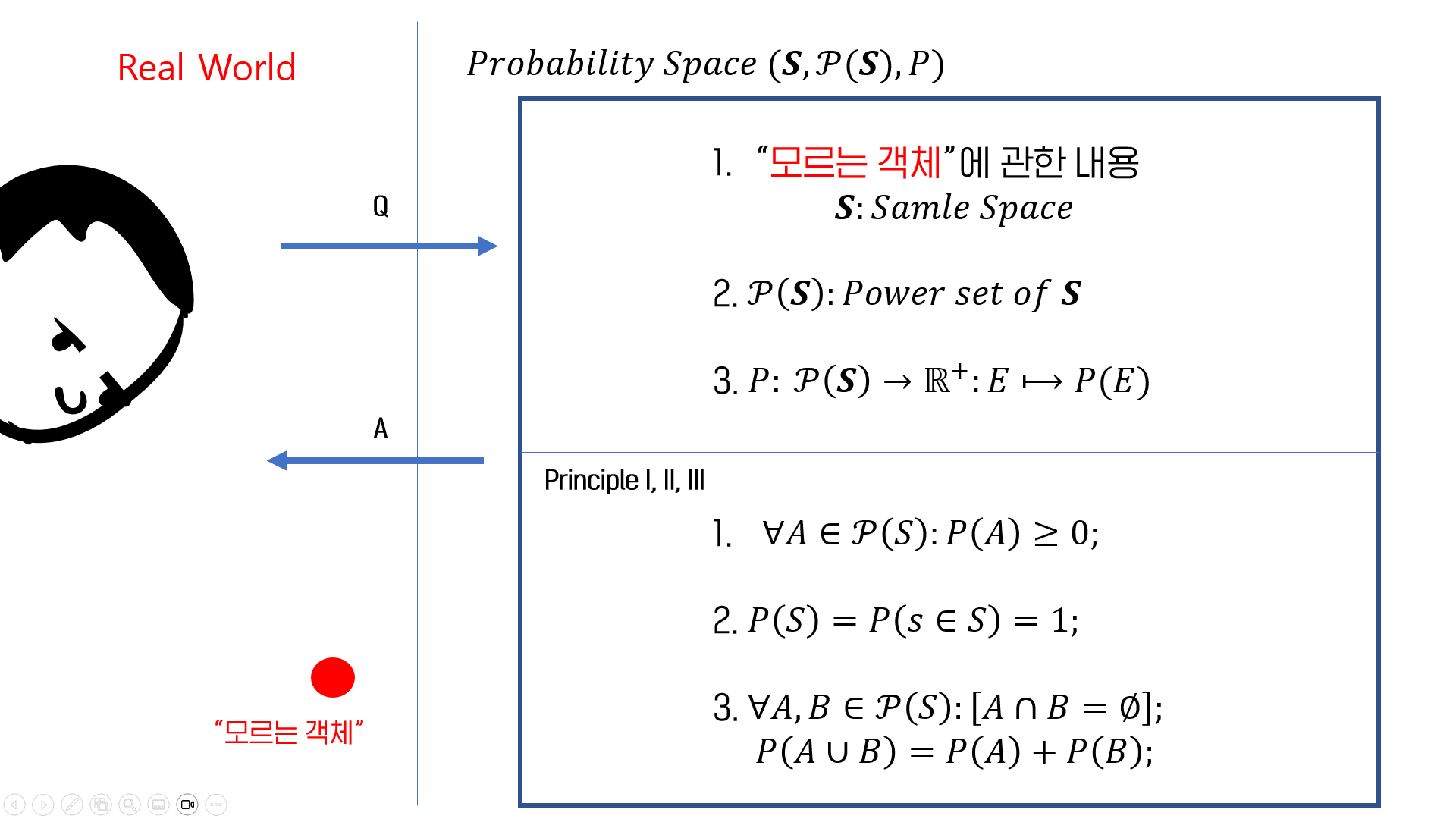
Figure 1 Real world user and probability space

  만약 왼쪽의 User가 오른쪽의 probability space에 임의의 질문을 했을 때 probability space가 결점이 없이 답변한다면, 우리는 이론상으로 정의된 probability space를 실생활에도 적용할 수 있을 것입니다! 즉, user은 지금까지의 probability space에 대한 정의를 내리는 것에 대한 강력한 동기를 제공해온 것입니다.

  실제로 분야를 불문한 모든 학문 연구에서는 통계 분석이 기본적으로 사용되고 있으며, 우리가 위에서 정의한 probability space를 기반으로 하고 있다는 사실을 확인할 수 있습니다.

  따라서 앞서 정의한 probability space가 잘 작동하는지 확인하기 위해 다음과 같은 세 가지 질문을 던졌다고 합시다. 우리가 정의한 probability space는 올바른 대답을 할 수 있을까요?

Question 1: Prove that $\forall A \in \mathcal{P}(S):P(A) \le 1;$

  Question 1이 필요한 이유: 앞서 확률의 상한이 1이라고 했는데, 이보다 커지면 우리는 제대로 확률 공간을 정의했다고 할 수 없습니다.

  Proof)

By using principle 3:

Hence we can conclude that:

따라서 우리는 확률 공간에 대해 했던 probability measure에 대한 정의를 다음과 같이 수정할 수 있습니다.

Question 2: Prove that if $A \subseteq B$ then $P(A) \le P(B)$;

  Question 2가 필요한 이유: 만약 $A \subseteq B$이면, $s \in B$라는 event가 일어났다는 사실은 $s \in A$이라는 event가 일어난 사실를 포함합니다. 따라서 $P(s \in B)$는 $P(s \in A)$보다는 같거나 커야 한다는 사실을 추론할 수 있습니다.

Proof)

Because $P(B \setminus A) \ge 0$:

Question 3: Prove that

  Question 3이 필요한 이유: 만약 우리가 $P(A)$와 $P(B)$를 알고 있을 때, $P(A \cup B)$를 계산하려면 논리적으로 1) $s \in A \setminus B$인 경우, 2) $s \in A \cap B$인 경우, 3. $s \in B \setminus A$인 경우 이 세 가지 가능성이 존재하며, 이들을 모두 더한 값이 바로 $P(A \cup B)$라는 사실을 추론할 수 있습니다.

Proof)
We know that:

and

Because

: we can let that

Hence

Conclusion: Is it enough?

  우리는 먼저 이론상으로 정의한 probability space가 여러 가지 확률에 대한 질문에 대해, 합리적인 답변을 할 수 있다는 사실을 확인할 수 있었습니다.

  위와 같은 규칙이 있으면, probability space는 outcome이 어떤 특성을 갖게 되는지에 대해 모든 답변을 할 수 있게 됩니다. 하지만 일상생활에서는 다음과 같은 순차적인, 파생적인 질문을 가지는 경우도 많다는 사실을 기억해야 합니다.

  1. Outcome이 주어진 특징을 만족한다는 사실을 확실히 알게 된다면, 그 때의 sample space와 probability measure은 어떤 순차적인 변화를 겪게 될까? (포커 게임에서 앞서 K가 4번 나왔다면, 승률엔 어떤 변화가 있을까?)

  2. 비행기가 특정 공역을 비행할 때, 레이더의 센서에 전압차가 발생한다. 그렇다면 센서에서 특정 전압차가 발생했을 때, 비행기가 특정 공역에 있을 확률은?

  첫 번째 문제는 outcome에 대한 추가적인 정보가 주어졌을 때 probability measure이 순차적으로 어떻게 변하는지에 대한 이야기이며, 두 번째 문제는 $\mathcal{P}(S)$의 원소들이 특정 함수에 mapping될 때, (혹은 system을 통과했을 때) 파생되는 outcome의 probability space는 어떻게 되는지에 대한 질문입니다.

  다음 시간에는 위에서 정의한 세 가지 규칙에 추가적으로 두가지 규칙을 더 소개해보겠습니다. 긴 글 읽어주셔서 감사합니다!