Random Process - Probability Measure에 관련된 규칙들 (2)

  이 글은 22-2학기 김운경 교수님의 Random Process 강의와 Peyton의 "Probability, Random Variables and Random Signal Principles" 4판을 참고하였음을 밝혀드립니다.

  저번 글에서는 probability space의 정의와 함께, 세 가지 principle에 대해 다루어 보았습니다. 이번 글에서는, user가 확률 공간에다가 추가적인 정보와 함께 질문을 던질 경우, probability는 이에 대한 답변을 위해 어떤 principle이 필요한지에 대해 이야기해보겠습니다.

Why Probability Space?

  저번 시간 우리는 user가 궁금해하는 질문에 답변을 효율적으로 하기 위해 probability space를 정의했다고 했습니다. 주어진 event에 대해, user는 outcome이 무엇인지 알지 못하며, 이 outcome을 모두 모은 집합을 sample space $S$라고 둡시다. 그렇다면 sample space의 power set $\mathcal{P}(S)$의 모든 원소를 real number으로 mapping시킨 것이 바로 확률입니다.

  즉, 확률은 outcome을 모르는 상황에서 outcome이 될 수 있는 모든 후보들의 무게를 재어보는 것이라고 할 수 있습니다. 직접 후보들의 무게를 비교하는 경우도 있지만, 어떤 경우에는 outcome이 원하는 특징을 가지는 지에 대해서도 무게를 재볼 수 있을 것입니다. 그 특징을 가진 모든 원소들을 모아둔 집합을 $A \subset S$라고 한다면, $P(s \in A)$가 바로 outcome이 해당 특징을 가질 확률이라고 정의할 수 있습니다.

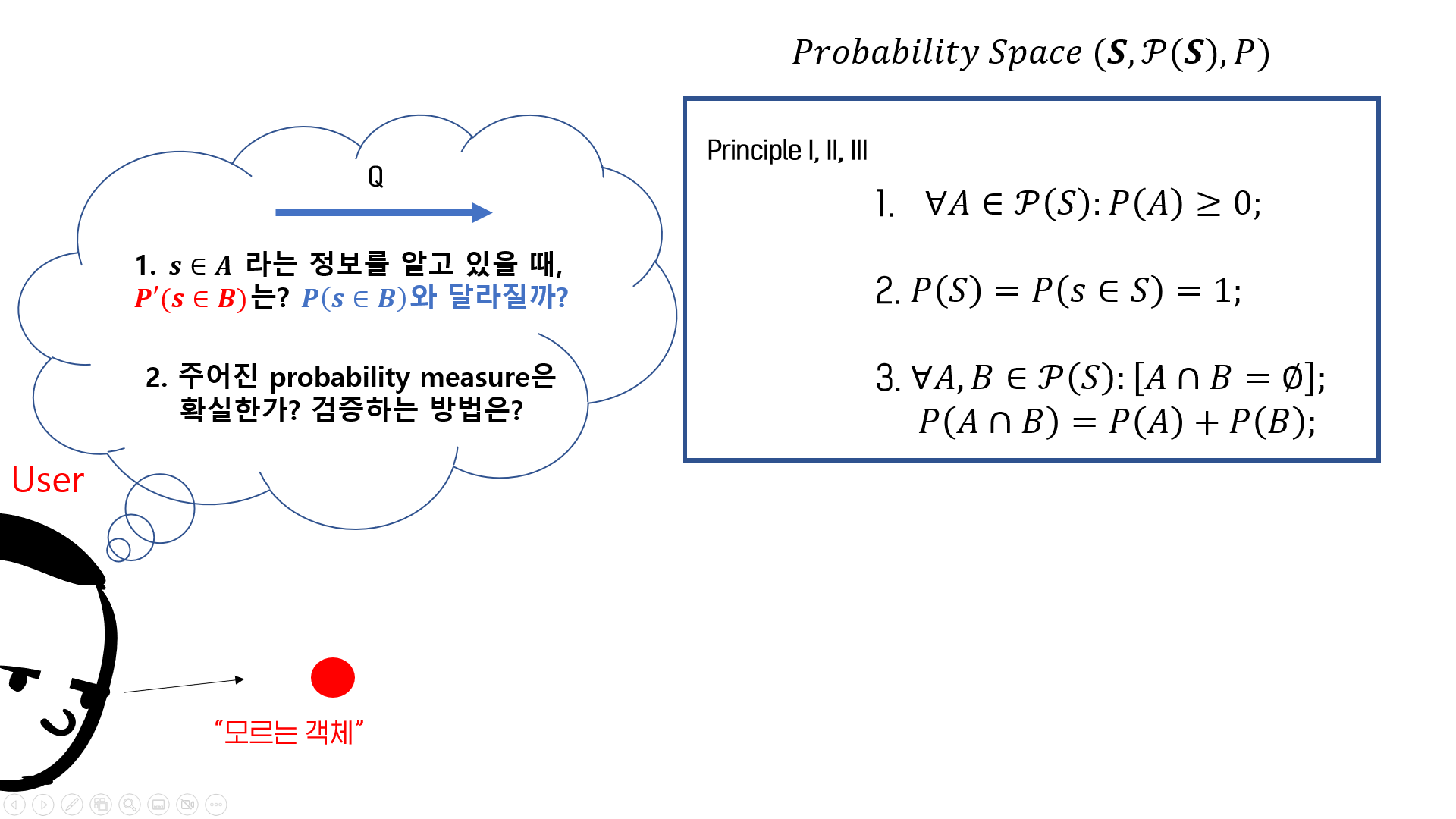
Is it enough?

  하지만 실생활에서 user는 이보다 더 복잡한 상황을 마주할 때가 훨씬 더 많습니다. 예를 들어, 모르는 event $s$에 대해, user가 그 event의 outcome이 어떠한 특징을 가지고 있다는 사실을 확실히 알고 있다고 합시다. 그 특징을 가진 모든 outcome을 모은 집합을 $A \subset S$라고 할 때, user는 이미 $s \in A$라는 정보를 알고 있다고 결론을 내릴 수 있을 것입니다. (단, 이 때 $A$는 공집합이 아니라는 가정이 필요합니다.)

  따라서 우리는 sample space가 $A$인 새로운 probability space를 생각하게 됩니다. 이러한 과정은 다음과 같은 그림으로 표현 가능합니다.

불완전한 user의 질문과 똑똑한 probability space.

  하지만 위 그림에서 중간의 power set이 $\mathcal{P}(A)$가 아닌 $\mathcal{S}$가 들어간 이유는 무엇일까요? 그 이유는 User의 '불완전한' 질문에서 답을 찾을 수 있습니다.

  예를 들어, 1부터 12까지 적힌 카드 중 하나의 카드를 뽑을 때, user는 그 카드가 짝수라는 사실을 이미 알고 있습니다. 이 때, user는 "과연 1부터 6사이의 수가 나올 확률은 얼마일까?"라는 질문을 떠올릴 수 있습니다.

  그렇다면, 1부터 12 중 짝수를 모은 집합을 $E$라고 하고, 1부터 6 사이의 수를 모은 집합을 $H$라고 한다면, user의 질문은 다음과 같다고 할 수 있습니다.

Given that $s \in E$ what is the probability that $s \in H$ ?

  그런데 이와 같은 질문은 다음 문장과 필요충분조건입니다.

Given that $s \in E$ what is the probability that $s \in H \cap E$ ?

  따라서 user는 probability space에 부분적인 정보를 제공하지만, probability space는 가장 적절한 대답을 해야 하기 때문에 새로운 probability space는 $(A, \mathcal{P}(A), P')$가 아닌 $(A, \mathcal{P}(S), P')$로 정의가 되는 것입니다.

새로운 probability measure.

  Probability space를 정의할 때 가장 중요한 일 중 하나가 바로 probability measure 함수를 정의하는 것입니다. 새로운 정보 $s \in A$가 주어졌을 때, probability space의 새로운 probability measure은 어떻게 변할까요?

  우리에게 필요한 가정은 의미없는 정보가 추가로 주어져도, 상대적인 확신의 정도는 변하지 않는다는 사실입니다. 예를 들어 우리는 문 앞에 서 있는 대학원생이 살아있다는 사실을 알고 있고, 연세대학교 학생보다는 고려대학교 학생일 확률이 두배라는 사실 또한 알고 있습니다.

  살아있는 모든 것들을 모은 집합을 $S$라고 할 때, 우리는 $(S, \mathcal{P}(S), P)$라는 확률 공간을 생각할 수 있습니다. 또한 고려대학교 대학원생을 모두 모은 집합을 $K \subset S$이라고 하고, 연세대학교 대학원생을 모두 모은 집합을 $Y \subset S$이라고 하면 다음과 같은 관계식이 성립합니다.

  이 때, 누군가가 와서 '사실 밖에 서 있는 분은 사람'이라는 정보를 제공한다고 합시다. 세상에 있는 모든 사람들을 모은 집합을 $M$이라고 할 때, 우리는 새로운 $(M, \mathcal{P}(M), P')$라는 확률 공간을 생각할 수 있습니다. 하지만 이러한 의미 없는 정보가 우리의 확신을 바꿀 수 있을까요?

  상식적으로 그럴 수 없습니다. 왜냐하면 우리는 $K, Y \subset S$를 만족하며, $K, Y \subset M$ 또한 만족한다는 사실을 이미 알고 있기 때문입니다. 따라서 이를 수식으로 정리하면 다음과 같을 것입니다.

  또한 이러한 현상은, '문 밖의 사람이 한국의 대학교를 다닌다'는 정보가 주어져도 동일하게 발생할 것입니다.

그래서 probability measure은?

  따라서 지금까지 살펴본 사실을 정리하면 다음과 같습니다. 원래 user은 궁금해하는 event $s$에 대해, $(S, \mathcal{P}(S), P)$이라는 probability space를 알고 있었고, 추가적으로 $s \in A$라는 정보를 알게 되어, $(A, \mathcal{P}(S), P')$라는 probability space를 정의해야 하는 상황에 놓여 있습니다. 그런데 $\forall B_1, B_2 \subset A, B_2 \neq \emptyset$에 대해, 다음과 같은 관계식이 만족합니다.

  그런데, 위와 같은 관계식을 조금 변형하면, 다음과 같음을 알 수 있습니다.

  따라서, 우리는 새로 정의한 probability space에 대한 complete knowledge를 알 수 있게 됩니다! 또한 probability measure을 불완전한 user의 질문을 고려하여 정의하면 다음과 같음을 쉽게 알 수 있습니다.

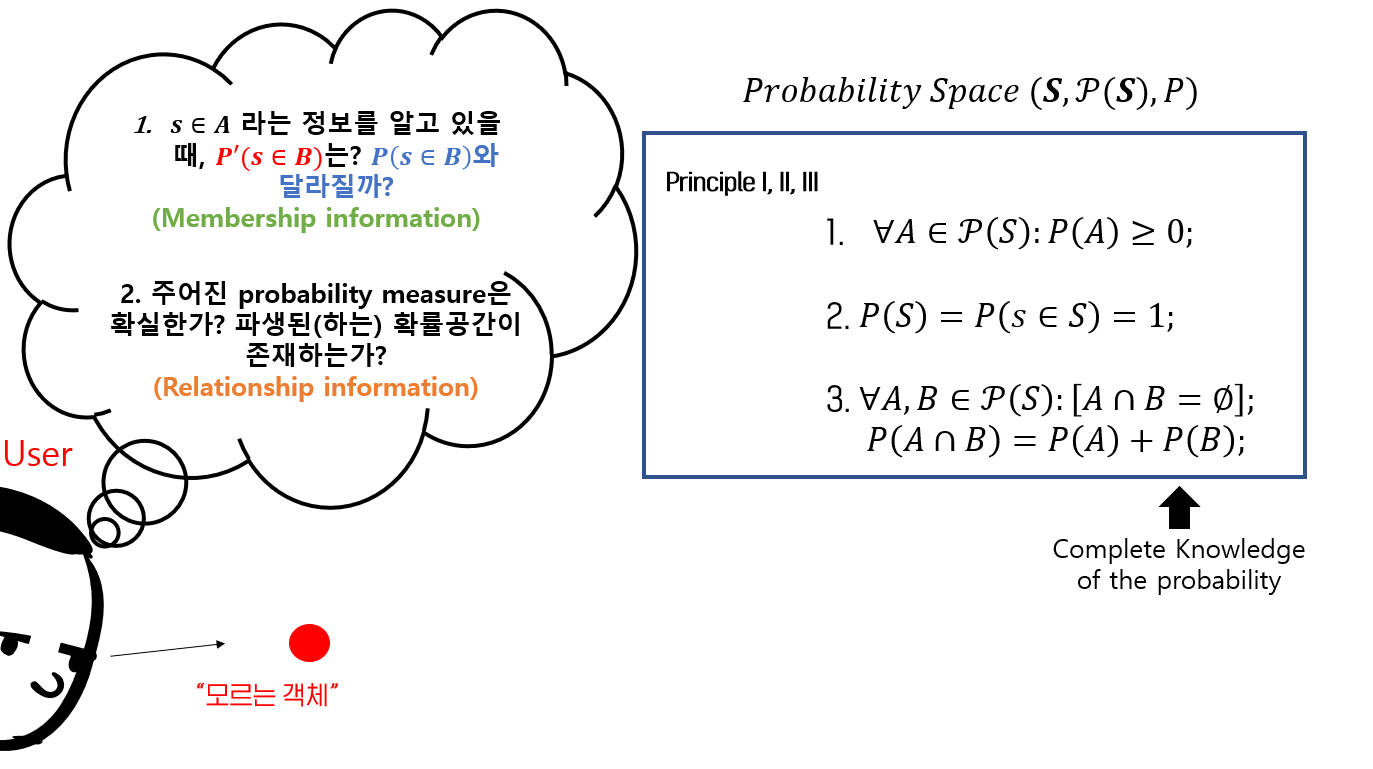
Conclusion.

  지금까지 membership information이 주어졌을 때 새로운 확률 공간이 어떻게 변하는지에 대해 살펴보았습니다. 다음 글에서는, 이러한 확률 공간이 make sense한지 살펴보고, 'relationship information'이 주어졌을 때는 확률 공간이 어떻게 변하는지 또한 살펴보겠습니다. 긴 글 읽어주셔서 감사합니다!