Convolution의 개념과 연산에 대하여

What is CNN(Convolutional Neural Network) ?

Convolutional Neural Network의 기원을 말하기 이전엔 퍼셉트론, 다층퍼셉트론 등의 개념들이 존재하지만, 이번 포스트에선 다루지 않습니다.

Convolutional Neural Network의 기원이자 첫 신호탄은 1950년대 하버드에서 진행되었으며, 고양이를 통해 동물의 시각적 정보가 어떠한 방식으로 처리되는지에 대해 연구했습니다.

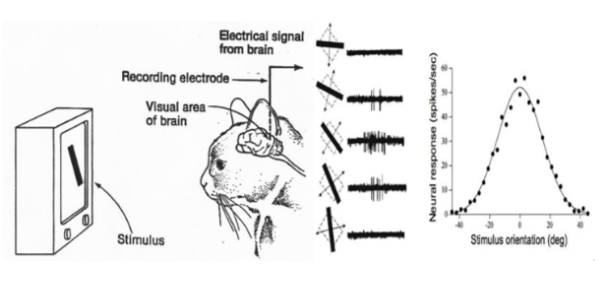
진행된 실험은 고양이의 뇌에 전극을 심어놓은 뒤 다양한 모양의 이미지를 보여주었을 때, 뉴런이 어떻게 활성화 되는지에 대해서 진행되었으며,

이러한 실험을 통해 동물이 시각적 정보를 받아들일 때, 전체 이미지를 한번에 해석하지 않고 이미지의 일부분을 다양하게 받아들인 뒤, 정보를 종합한다는 것을 알게되었습니다.

해당 실험 결과를 바탕으로 기존 퍼셉트론 기반의 인공신경망에서 합성곱 신경망(CNN : Convolutional Neural Network)을 통해 이미지를 인식하는 방법으로 변화시키고 개선시킬 수 있게되었습니다.

이러한 훌륭한 실험 결과와 함께 짚고 넘어가야 할 점이 존재하는데, 그것은 바로 합성곱 신경망이 왜 필요한가? 입니다. 이를 위해선 퍼셉트론으로 이미지를 다루는게 얼마나 비효율적인지 알아야 합니다.

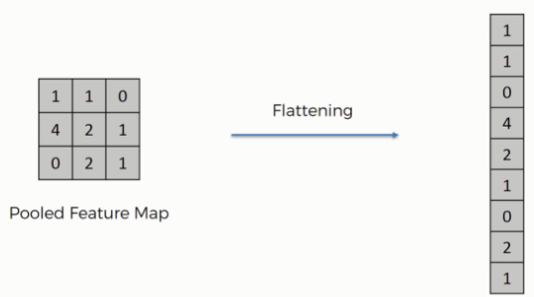
과거 합성곱 신경망이 등장하기 이전엔 다층 퍼셉트론을 활용하여 이미지를 다루었습니다. 2차원 형태의 이미지를 그대로 사용하는 것이 아닌 평평하게 펴서 활용했다는 의미로 볼 수 있습니다.

일반적으로 이미지는 2차원 형태의 배열로써, 순차적인 값들이 연관되어있지 않고 중심 픽셀과 인근 픽셀들이 서로가 서로에게 중요한 연관관계이다. 라고 할 수 있습니다.

하지만 이러한 2차원 정보를 평평하게 펴서 1차원 형태로 다층 퍼셉트론에서 활용하는 경우 계산을 위한 파라미터 수가 이미지의 크기와 비례하여 증가되고, 이미지가 갖는 위치 정보 또한 손실됩니다.

결과적으로 입력되는 이미지의 크기를 곱해준만큼의 파라미터가 필요하기 때문에 과적합과 싸워야하며, 이미지의 위치 정보가 사라지기 때문에 연산을 통해 도출된 정확도 또한 기대에 못미치게 됩니다.

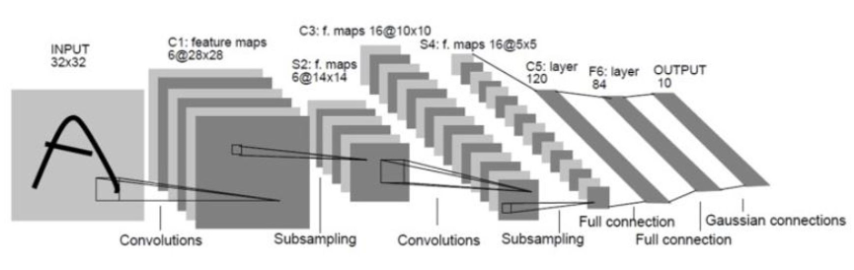
이러한 다층 퍼셉트론의 단점을 보완하기 위해, 앞선 시각 실험을 기반으로 1990년대 최초의 합성곱 신경망(CNN: Convolutional Neural Network) LeNet이 등장했으며, 이는 크나큰 발전을 이룩했습니다.

최초의 합성곱 신경망을 시작으로 이미지 인식 성능 개선, 계산량 감소 등 다양한 발전을 이끌어냈으며, 이러한 합성곱 신경망은 현재까지도 널리 사용되는 이미지 분석 방법으로 알려져 있습니다.

CNN의 발전 과정은 이 이외에도 상세한 스토리들이 있지만 여기서 마무리한 뒤, 다음 파트에서 CNN에 대한 조금 더 상세한 개념들을 다뤄보도록 하겠습니다.

Convolution(2D) 레이어의 연산, 파라미터 및 관련 레이어

앞서 LeNet을 통해 합성곱 신경망의 개념과 연산에 대해 간단하게 확인해보았지만, 내부적인 연산 과정은 어떻게되고 값은 어떻게 표현되는지 까진 알기 어려웠습니다.

이번 파트에선 이러한 Convolution 연산에 대해 다뤄보며, 이번 파트에서 다루는 Convolution 연산은 이미지 연산에서 사용되는 2D를 기반으로 합니다.

실 생활에서 시각적으로 받아들이는 이미지, 영상 정보들은 모두 픽셀(Pixel)이라는 단위를 가지며, 빛의 3원색으로 알려진 빨간색, 초록색, 파란색 픽셀 정보가 담겨져 있습니다. 이를 RGB 채널이라 합니다.

이미지는 앞서 설명한 채널 정보는 물론, 일정한 크기의 너비와 높이를 갖습니다.

Convolution 연산은 이러한 이미지의 너비, 높이 및 채널 정보를 입력 데이터로 사용하며, 필터(filter, 학습하는 파라미터)를 통해 계산과 학습을 반복해가며 점진적으로 이미지를 해석하는 방법을 학습하게 됩니다.

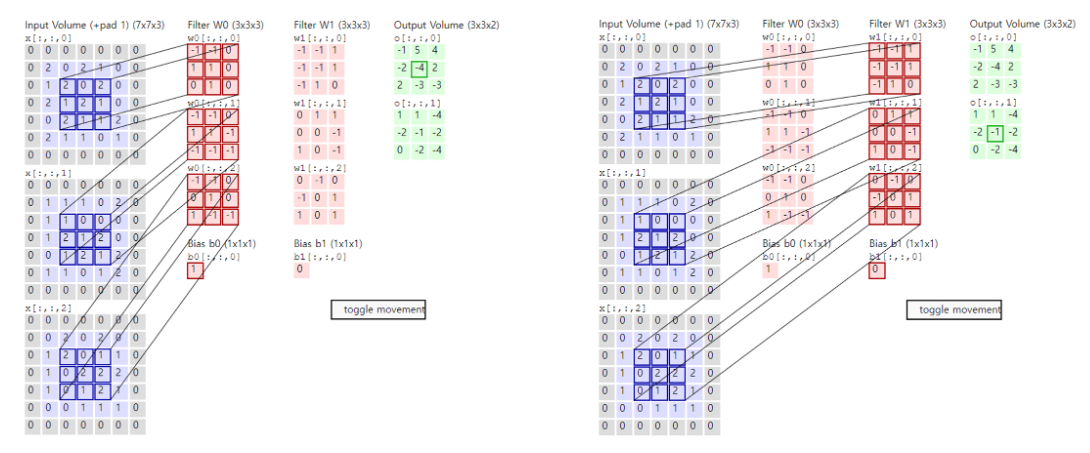
위에서 설명한 필터 개념이 Convolution 연산의 핵심이라 할 수 있으며, 위 이미지를 통해 이미지와 필터가 어떻게 계산되는지 시각적으로 이해해볼 수 있습니다.

입력 이미지에 대해 Convolution 연산을 수행하기 위해선 특정 크기로 정의된 필터(filter)가 필요하며, 일반적으로 필터는 $N * N$ 형태의 정사각 형태로 이루어져 있습니다.

이러한 Convolution 필터에 대해, $N * N$ 크기의 필터가 보는 영역을 주로 receptive field(수용 영역)라고 합니다. 논문 등의 여러 자료에서 자주 등장하는 개념이기에 간단하게 소개 드렸습니다.

그렇다면 입력 이미지와 필터만 정의된 상태에서 바로 Convolution 연산을 수행할 수 있을까요? 연산 자체는 가능하지만 원하는 형태의 결과물을 만들기 위해선 몇가지 인자를 함께 사용해야 합니다.

Convolution 연산 내에서 핵심적으로 사용되는 인자들은 Filter size(kernel size), Stride, Padding이며, 이러한 인자들은 어떠한 속성을 갖는지 확인해보겠습니다.

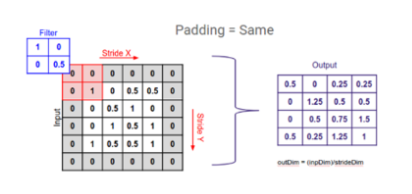
Padding은 입력 이미지에 대해 연산을 수행하는 과정에서 필터 혹은 이미지의 크기로 인해 연산 전/후의 이미지 크기가 다른 경우를 대비하기 위함이며, 모자란 크기만큼 가장자리에 빈 값을 추가합니다.

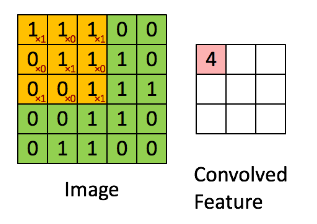
만약 너비, 높이가 각각 5의 크기를 갖는 이미지에 대해 Padding을 적용하지 않은 상태로 너비, 높이 3의 크기를 갖는 필터로 연산을 수행하게 된다면, 그 결과는 어떻게 될까요?

위 이미지의 결과와 같이 원본 이미지의 크기를 유지하지 못하게되고, 이는 결국 Convolution 연산을 거듭하여 진행할 수록 원본 이미지의 정보가 손실됨(크기가 점점 작아짐)을 의미하게 됩니다.

또한 Convolution 연산의 특성 상, 가장자리에 존재하는 픽셀 연산은 필터를 통해 계산되는 과정에서, 중심부에 존재하는 픽셀에 비해 연산에 참여하는 횟수가 적어, 영향 자체가 작아지는 문제도 있습니다.

이러한 원치 않는 정보 손실을 위해 사용되는 것이 Padding이며, 원하는만큼 가장자리에 0의 값을 넣어줄 수 있으며 padding=’same’ 인자의 경우, 이를 자동으로 넣어주게 됩니다.

Padding에 대한 설명은 간략하게 여기서 마무리하고, 다음 개념으로 Stride에 대해 알아보겠습니다. Stride는 입력 이미지에 대해 연산을 수행하는 과정에서 필터를 움직이는 크기를 의미합니다.

Stride를 2 이상의 값을 활용하는 경우 Padding을 same으로 적용하더라도 출력 이미지 크기는 무조건 줄어들게 됩니다. 이에 대해선 추후 코드 예제에서 확인해보도록 하겠습니다.

다음 설명할 것은 Filter이며, Filter의 개념은 입력 이미지에 대한 Convolution 연산을 수행하는 과정에서 가장 핵심적인 인자이며, 가장 중요한 점으로는 학습되는 파라미터(가중치)의 의미를 갖는 것입니다.

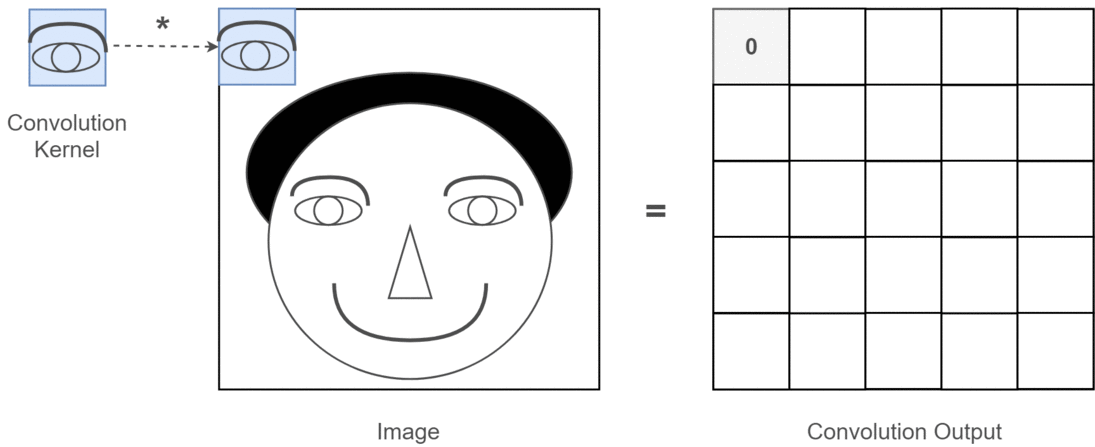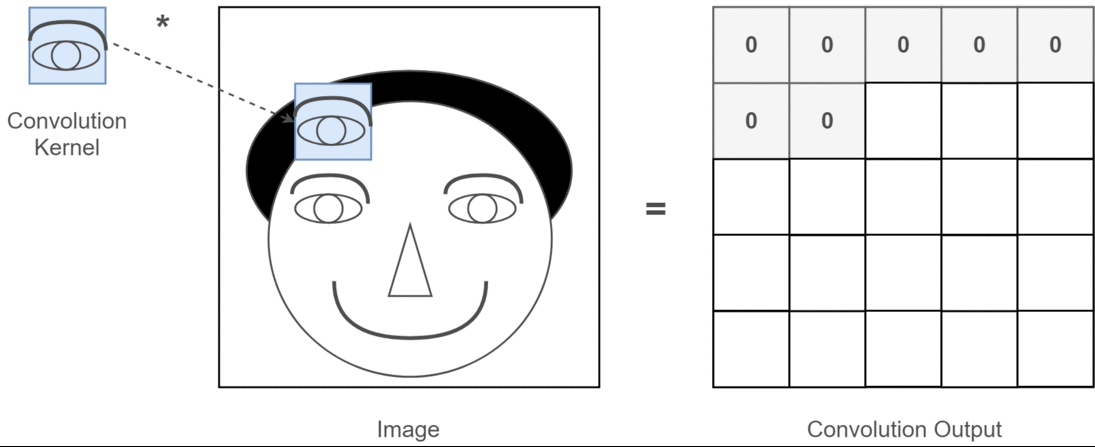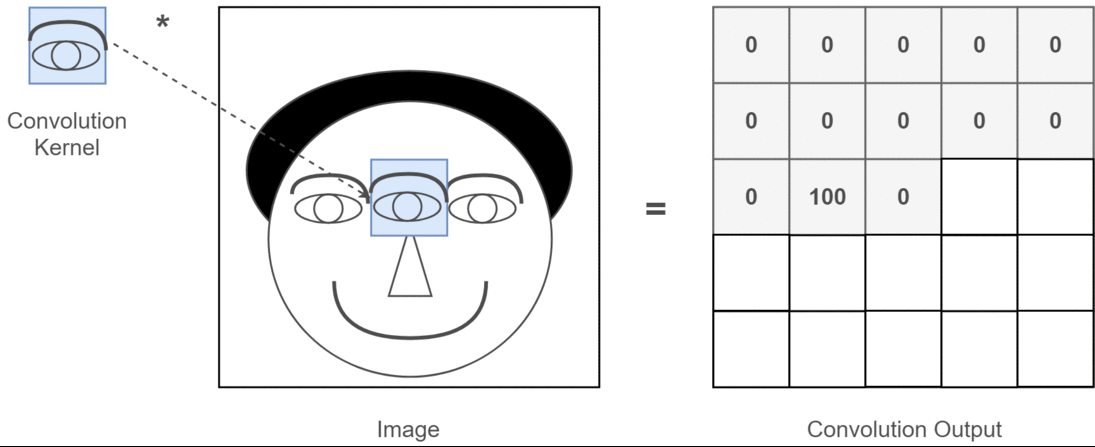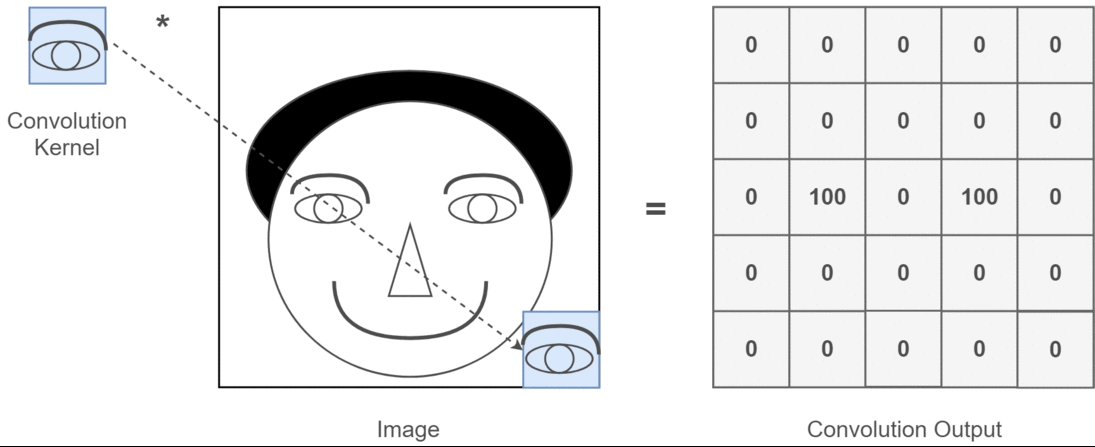
Convolution의 핵심은 이미지를 효과적으로 분석하는 방법을 배우는 것이지만, 결과적으론 이미지를 구성하는 핵심 요소들을 필터로 학습하는 것을 의미하며, 위 GIF에선 필터 연산을 나타내고 있습니다.

여기서 필터가 이미지의 핵심적인 요소들을 학습한다는 것이 어떠한 의미인지, 중요한 개념이기 때문에 이를 조금 더 풀어 설명해보겠습니다

필터(파라미터)를 통해 픽셀 연산(이미지)을 수행한다고 가정했을 때, 필터가 0인 부분은 영향이 전혀 없을 것이며, 필터가 1인 부분은 필터가 학습한 이미지에서의 핵심 요소라고 할 수 있습니다.

위 그림 A의 필터 크기가 $5 * 5$ 라고 했을 때, 가로 줄이 그어진 필터의 가중치는 오른쪽 이미지와 같은 가중치를 갖는다고도 할 수 있습니다. 또한 이러한 필터 가중치는 지속적으로 변화하며 학습됩니다.

물론 Convolution 연산을 일부 영역에 대해 수행하고 모든 값과 편향을 더해서 결정되지만, 위 A 이미지의 가중치를 갖는 필터의 연산이 수행된다면 결과 이미지에선 가로 직선의 형태가 부각되게 됩니다.

결국 필터란 이미지를 해석하기 위해 수십, 수백개로 나누어 정보를 추출하는 과정(가로, 세로 등)이라고 할 수 있으며, 이러한 정보를 잘 추출해낼 수 있는 필터를 학습하는 것이 CNN 학습의 목적입니다.

그렇다면 Convolution 연산만을 계속 수행한다면 이미지를 효과적으로 분석할 수 있을까요? 현재까지의 설명으로는 가능할 것처럼 느껴지지만, 실제 학습 과정에선 그렇지 않습니다.

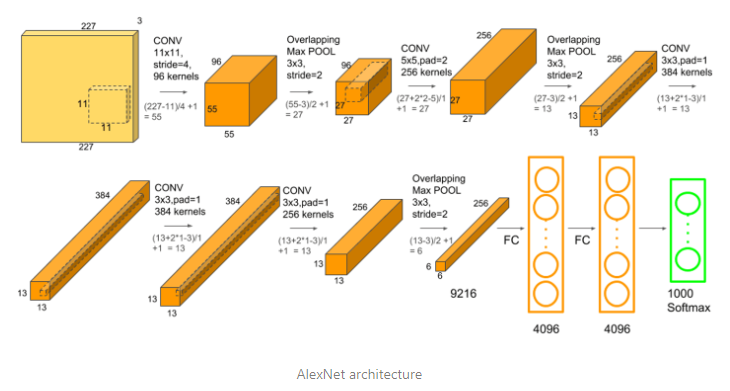
이미지의 크기가 유지된다면 많은 연산량을 계속 갖게됨은 물론이며, 정보는 점점 깊어지는데 표현력은 그대로이니 파라미터는 결국 과적합되는 방향으로 학습됩니다. 이 때, 사용되는 것이 Pooling 입니다.

월드컵과 같은 대회에서 수상자를 가려야 한다고 가정했을 때 예선, 본선, 8강, 4강 등 .. 많은 팀들이 탈락하며 우수한 경기력을 갖는 팀들이 선별될 것이고, 해당 팀들 또한 팀워크가 점점 올라가 더욱 잘해질 것 입니다.

Convolution에서 추구하는 연산의 개념이 위의 예시와 같으며, 이미지에서 뽑아낸 다양한 정보를 결합하고 보완해가며 보다 이미지를 잘 표현할 수 있는 좋은 특징들을 활용하는 것이라 할 수 있습니다.

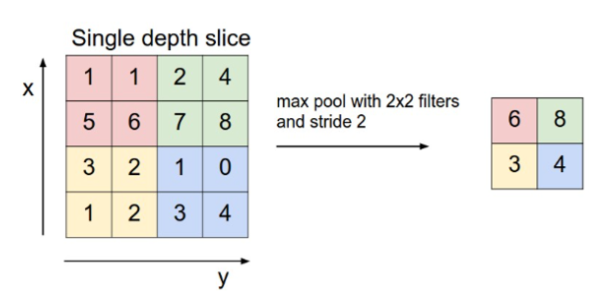
Conv 연산을 통해 산출된 결과물을 feature 혹은 activation map이라 하며, 이렇게 만들어진 feature map을 기반으로 정보를 압축할 때, Pooling이 사용됩니다. Pooling은 가장 큰 값을 남기는 Max Pooling이 주로 활용됩니다.

Pooling은 앞선 Convolution 연산과 동일하게 filter와 stride를 가지며, 유사한 연산 구조를 가지지만 별도로 학습되는 파라미터는 존재하지 않으며, filter 크기 내 픽셀 값을 활용한 연산을 수행합니다.

위 이미지에선 Max Pooling 수행 과정에 대해 나타내고 있습니다. 모든 Pooling에서 반드시 Stride를 2 이상의 값으로 주어야 하는건 아니며 Padding 또한 설정할 순 있지만, Stride 2를 가장 많이 활용합니다.

최근 Pooling을 사용하지 않고, Pooling을 사용할 위치에서 Convolution 연산의 Stride를 2로 주는 방법을 주로 활용합니다. 단순 알고리즘적인 방법보다 파라미터를 활용하는 것이 좋은 성능을 도출하기 때문인 것 같습니다.

이번 파트에선 Convolution 연산과 함께 활용되는 여러 인자 혹은 개념들을 살펴보았습니다. 이 외에도 Flatten, Global Average Pooling 등 여러 개념이 존재하지만, 다른 포스트에서 조금 더 깊게 다루도록 하겠습니다.

다음 파트에선 Convolution 레이어의 Filter 가중치가 실제로 어떻게 생겼는지, 앞선 Padding 등의 개념은 실제 어떻게 만들어지는지 코드와 결과로 확인해보겠습니다.

Convolution 가중치와 tensorflow 예제

여러 자료를 통해 이해하는 Convolution 연산 방식과 Convolution 레이어가 실제로 동작하는 방식은 약간 다르게 느껴질 수 있습니다. 또한 Padding과 Stride에 대한 이해가 부족할 수도 있습니다.

이번 파트에선 앞서 설명했던 내용들에 대해 코드 기반의 추가 설명과 Convolution 레이어가 갖는 실제 가중치가 어떠한 형태인지 확인해보도록 하겠습니다.

일상 생활에서 쉽게 접할 수 있는 카메라 이미지를 우리는 보통 이미지, 2D 이미지, 혹은 2차원 이미지라고 부르고 있습니다. 이러한 이미지는 앞선 개념인 빛의 3원색을 포함해 3차원 개념을 갖고 있습니다.

Tensorflow, Pytorch에서 사용되는 이미지는 모두 3차원 배열의 형태를 갖고 있으며, 이러한 이미지의 묶음 혹은 집합이라는 의미로 배치사이즈 개념이 추가되어 4차원 데이터라고 정의하게 됩니다.

아래 예제 코드에선 이러한 배경을 밑바탕으로 하는 4차원 이미지 집합을 데이터로 사용하며, 앞서 설명한 개념인 Padding, Stride에 대한 코드를 나타내고 있습니다.

# 샘플 데이터 지정
# 128 * 128 * 3 크기의 이미지 32장
array_2d = np.random.normal(0, 1, size=(32, 128, 128, 3)).reshape(32, 128, 128, 3)
array_2d_zero_padding = layer_zero_padding(np.random.normal(0, 1, size=(32, 128, 128, 3)).reshape(32, 128, 128, 3))
print('No Padding shape : ', array_2d.shape, 'Using Padding shape : ', array_2d_zero_padding.shape, '\n')

>>> output 
No Padding shape :  (32, 128, 128, 3) Using Padding shape :  (32, 130, 130, 3)

# filter 개수 : 16, kernel 크기 : 3x3, stride : 1
layer_padding_same = layers.Conv2D(16, 3, 1, padding='same', activation='relu')
layer_padding_valid = layers.Conv2D(16, 3, 1, padding='valid', activation='relu')
layer_padding_stride = layers.Conv2D(16, 3, 2, padding='same', activation='relu')
layer_zero_padding = layers.ZeroPadding2D(padding=1)

# 2D Convolution 연산 수행
layer_padding_same_output = layer_padding_same(array_2d)
layer_padding_valid_output = layer_padding_valid(array_2d)
layer_zero_padding_valid_output = layer_padding_valid(array_2d_zero_padding)
layer_padding_stride_output = layer_padding_stride(array_2d)
print('Padding Same : ', layer_padding_same_output.shape, 'Padding Valid : ', layer_padding_valid_output.shape)
print('Zero Padding Valid : ', layer_zero_padding_valid_output.shape, 'Zero Padding + Stride 2 : ', layer_padding_stride_output.shape)

>>> output 
Padding Same :  (32, 128, 128, 16) Padding Valid :  (32, 126, 126, 16)
Zero Padding Valid :  (32, 128, 128, 16) Zero Padding + Stride 2 :  (32, 64, 64, 16)

4차원 이미지 집합에 대해 Padding을 적용하지 않은 Padding Valid Convolution 연산을 수행하는 경우, 기존 128 128 크기의 이미지가 126 126 크기로 줄어든 것을 확인할 수 있습니다.

이러한 결과와 반대로 Padding Same Convolution 연산을 수행한 결과에선 128 128 이미지가 128 128 형태 그대로 출력되는 것을 확인할 수 있습니다. 이 때, Padding Same의 역할은 무엇일까요?

Padding Same은 연산을 수행할 Convolution 레이어의 Filter 크기에 맞추어 사전에 미리 Zero Padding을 씌워주는 작업을 의미하며, 위의 코드에서도 확인할 수 있습니다.

Zero Padding을 추가해준 데이터를 기준으로 Padding Valid Convolution 연산을 수행했을 때, Padding Same 연산을 수행한 결과물과 동일한 크기의 output을 도출하는 것을 확인할 수 있습니다.

또한 Stride 연산 실험을 위해 Padding Same Convolution 연산에서 Stride 값을 2로 설정해주었더니, Padding Same을 적용해주었음에도 이미지가 절반의 크기로 줄어든 것을 확인할 수 있습니다.

이러한 실험을 통해 Stride는 Padding과 관계없이, 입력 이미지의 정보를 축소시키는 것을 확인할 수 있었으며 Pooling 연산 또한 Stride와 동일한 결과물을 도출합니다.

앞선 Padding, Pooling, Stride의 부족한 설명이 충족되셨길 바라며, 다음으론 Convolution 연산과 가중치에 대해 확인해보겠습니다.

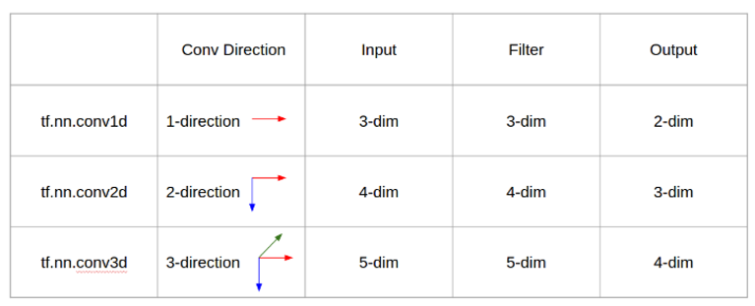
Convolution 레이어가 갖는 가중치, 필요로 하는 데이터의 형태, 연산 방향 등은 위 이미지의 자료를 통해 확인할 수 있습니다. 하지만 무엇을 의미하는지 잘 이해하기 어렵습니다.

아래 코드를 통해 각각의 Convolution 연산과 결과물, 그리고 가중치와 편향의 형태에 대해서도 확인해보겠습니다.

# Example to Convolution 1D
# filter 개수 : 16, kernel 크기 : 3, stride : 1
layer_padding_same = layers.Conv1D(16, 3, 1, padding='same', activation='relu')
layer_padding_valid = layers.Conv1D(16, 3, 1, padding='valid', activation='relu')
layer_padding_stride = layers.Conv1D(16, 3, 2, padding='same', activation='relu')

# 샘플 데이터 지정
# 32개의 샘플, 각 24번의 타입 스텝, 1개의 변수
# ex) 32개의 지역에서 1시간 단위로 기록된 온도 데이터
array_1d = np.random.normal(0, 1, size=(32, 24)).reshape(32, 24, 1)
print('Array shape : ', array_1d.shape)
>> Array shape :  (32, 24, 1)

# 1D Convolution 연산 수행
layer_padding_same_output = layer_padding_same(array_1d)
layer_padding_valid_output = layer_padding_valid(array_1d)
layer_padding_stride_output = layer_padding_stride(array_1d)
print('Padding Same shape : ', layer_padding_same_output.shape, 'Padding Valid shape : ', layer_padding_valid_output.shape, 'Stride 2 shape : ', layer_padding_stride_output.shape)
>> Padding Same shape :  (32, 24, 16) Padding Valid shape :  (32, 22, 16) Stride 2 shape :  (32, 12, 16)

# 가중치 shape
print('Weights shape : ', layer_padding_same.weights[0].shape, 'Biases shape : ', layer_padding_same.weights[1].shape)
>> Weights shape :  (3, 1, 16) Biases shape :  (16,)

Convolution 1D 연산은 단방향 연산으로써 주로 시계열 데이터에서 활용되며, 배치 차원이 포함된 3차원 데이터를 입력으로 받아 처리하게 됩니다.

위 예제에서 사용된 데이터를 풀어 설명한다면, 24시간동안 32개의 지역에서 1시간 단위로 수집된 온도 데이터(1개의 변수)라고 할 수 있습니다.

이러한 데이터는 (32, 24)의 차원을 갖지만, Convolution 연산의 특성 상 필터의 수만큼 차원 정보가 늘어나야하기 때문에 변수 축을 추가로 붙여 (32, 24, 1) 형태로 넣어주게 됩니다.

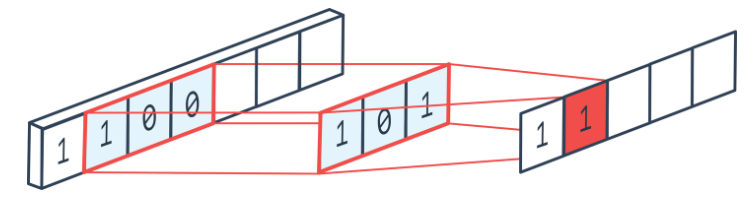
이러한 3차원 데이터를 활용해 Convolution 1D 연산을 수행했을 때, Padding 여부에 따라 (32, 24, 16) 혹은 (32, 22, 16)의 결과물을 나타내고, Stride가 2인 경우 (32, 12, 16)의 결과물을 도출합니다.

단방향 연산이기 때문에 입력 데이터의 데이터 수(24개→22개)가 직접적으로 변화되며, Filter 또한 단방향 연산을 위한 형태라고 할 수 있습니다.

실제 가중치는 (3, 1, 16)의 형태이며, 이는 (3, 1) 크기의 Filter가 16개 존재한다는 의미로 해석할 수 있으며, 이 때, 1은 무시한 상태로 3의 크기를 갖는 1차원 Filter라고도 할 수 있습니다.

# Example to Convolution 2D
# filter 개수 : 16, kernel 크기 : 3x3, stride : 1
layer_padding_same = layers.Conv2D(16, 3, 1, padding='same', activation='relu')
layer_padding_valid = layers.Conv2D(16, 3, 1, padding='valid', activation='relu')
layer_padding_stride = layers.Conv2D(16, 3, 2, padding='same', activation='relu')

# 샘플 데이터 지정
# 128 * 128 * 3 크기의 이미지 32장
array_2d = np.random.normal(0, 1, size=(32, 128, 128, 3)).reshape(32, 128, 128, 3)
print('Array shape : ', array_2d.shape)
>> Array shape :  (32, 128, 128, 3)

# 2D Convolution 연산 수행
layer_padding_same_output = layer_padding_same(array_2d)
layer_padding_valid_output = layer_padding_valid(array_2d)
layer_padding_stride_output = layer_padding_stride(array_2d)
print('Padding Same shape : ', layer_padding_same_output.shape, 'Padding Valid shape : ', layer_padding_valid_output.shape, 'Stride 2 shape : ', layer_padding_stride_output.shape)
>> Padding Same shape :  (32, 128, 128, 16) Padding Valid shape :  (32, 126, 126, 16) Stride 2 shape :  (32, 64, 64, 16)

# 가중치 shape
print('Weights shape : ', layer_padding_same.weights[0].shape, 'Biases shape : ', layer_padding_same.weights[1].shape)
>> Weights shape :  (3, 3, 3, 16) Biases shape :  (16,)

Convolution 2D 연산은 너비, 높이에 대한 양방향 연산으로써 주로 이미지 데이터에서 활용되며, 배치 차원이 포함된 4차원 데이터를 입력으로 받아 처리하게 됩니다.

위 예제에서 사용된 데이터를 풀어 설명한다면, 128 * 128의 크기를 갖는 RGB 이미지가 32개 모여있는 이미지 데이터 집합이라고 할 수 있습니다.

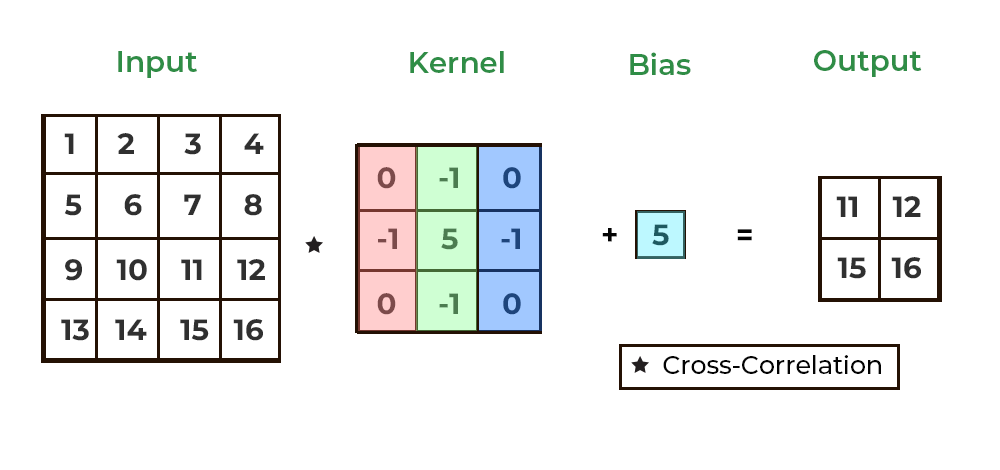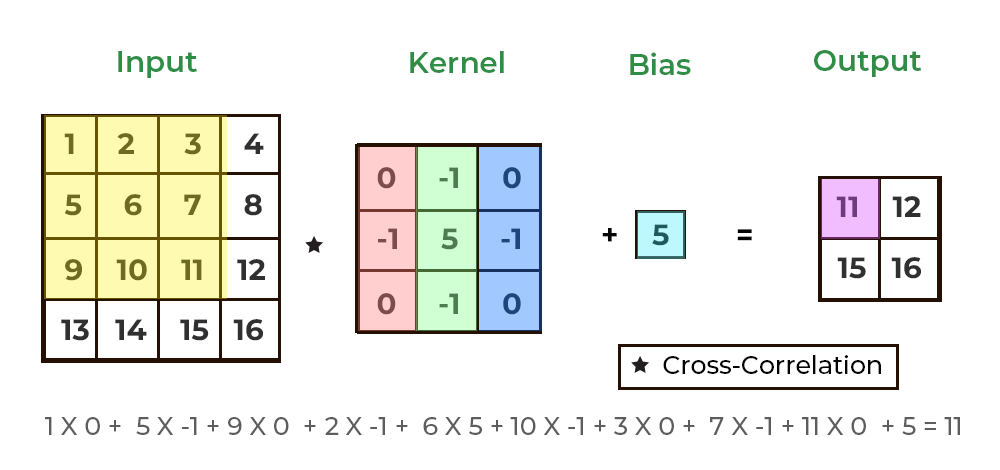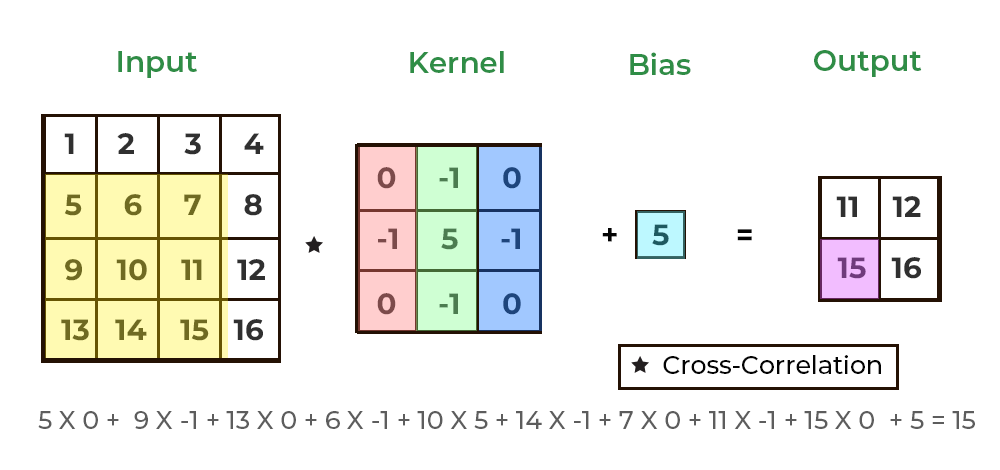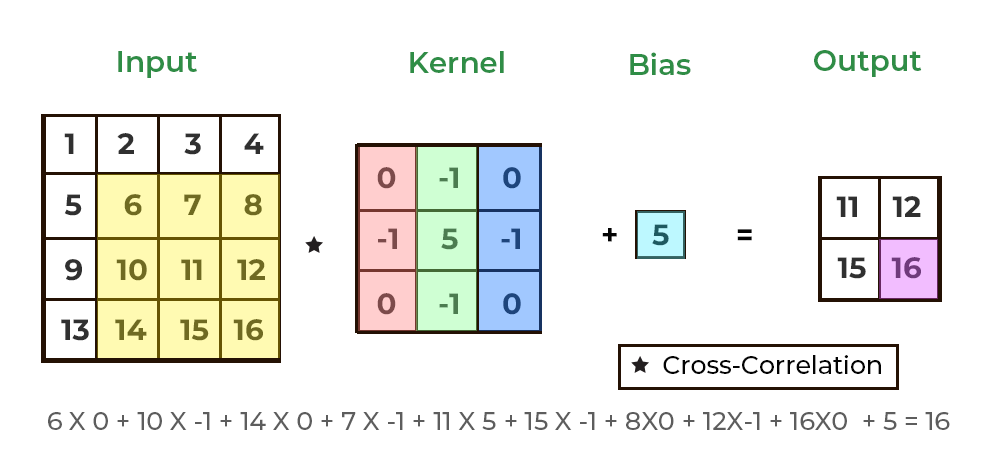
이러한 4차원 데이터를 활용해 Convolution 2D 연산을 수행했을 때, Padding 여부에 따라 (32, 128, 128, 16) 혹은 (32, 126, 126, 16)의 결과물을 나타내고, Stride가 2인 경우 (32, 64, 64, 16)를 도출합니다.

앞선 Convolution 1D와 유사하게 동작하지만, 3차원 이미지에 대해 동작하기 때문에 RGB 채널은 Filter의 개수만큼 변화하고 이미지의 크기는 Filter 크기와 Padding 여부에 따라 변화됩니다.

Convolution 2D의 가중치는 (3, 3, 3, 16)의 형태이며, 이는 (3, 3, 3) 크기의 Filter가 16개 존재한다는 의미로 해석할 수 있습니다. (3, 3, 3) Filter는 너비, 높이, RGB 채널에 대해 각각 연산되게 됩니다.

# Example to Convolution 3D
# filter 개수 : 16, kernel 크기 : 3x3, stride : 1
layer_padding_same = layers.Conv3D(16, 3, 1, padding='same', activation='relu')
layer_padding_valid = layers.Conv3D(16, 3, 1, padding='valid', activation='relu')
layer_padding_stride = layers.Conv3D(16, 3, 2, padding='same', activation='relu')

# 샘플 데이터 지정
# 128 * 128 * 3 크기의 동영상에 32장의 프레임이 존재하며, 이러한 동영상이 4개 존재
array_3d = np.random.normal(0, 1, size=(4, 32, 128, 128, 3)).reshape(4, 32, 128, 128, 3)
print('Array shape : ', array_3d.shape)
>> Array shape :  (4, 32, 128, 128, 3)

# 3D Convolution 연산 수행
layer_padding_same_output = layer_padding_same(array_3d)
layer_padding_valid_output = layer_padding_valid(array_3d)
layer_padding_stride_output = layer_padding_stride(array_3d)
print('Padding Same shape : ', layer_padding_same_output.shape, 'Padding Valid shape : ', layer_padding_valid_output.shape, 'Stride 2 shape : ', layer_padding_stride_output.shape)
>> Padding Same shape :  (4, 32, 128, 128, 16) Padding Valid shape :  (4, 30, 126, 126, 16) Stride 2 shape :  (4, 16, 64, 64, 16)

# 가중치 shape
print('Weights shape : ', layer_padding_same.weights[0].shape, 'Biases shape : ', layer_padding_same.weights[1].shape)
>> Weights shape :  (3, 3, 3, 3, 16) Biases shape :  (16,)

Convolution 3D 연산은 너비, 높이, 깊이(영상이라면 프레임)에 대해 3방향 연산을 수행합니다. 주로 동영상 데이터에서 활용되며, 배치 차원이 포함된 5차원 데이터를 입력으로 받아 처리하게 됩니다.

위 예제에서 사용된 데이터를 풀어 설명한다면, 128 * 128의 크기를 갖는 RGB 이미지가 32개 모여있는 동영상이 총 4개 있는 동영상 데이터 집합이라고 할 수 있습니다.

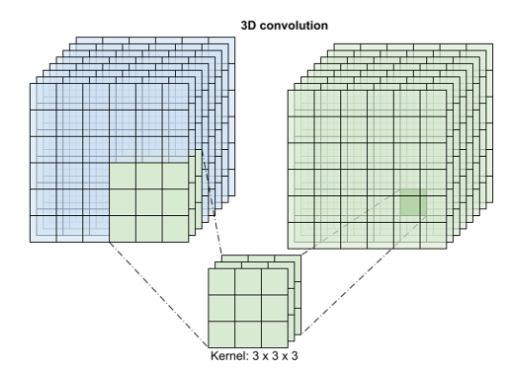
이러한 5차원 데이터를 활용해 Convolution 3D 연산을 수행했을 때, Padding 여부에 따라 (4, 32, 128, 128, 16) 혹은 (4, 30, 126, 126, 16)의 결과물을 나타내고, Stride가 2인 경우 (4, 16, 64, 64, 16)를 도출합니다.

4차원 영상 데이터에 대한 연산을 수행하기 때문에 RGB 채널은 Filter의 개수만큼 변화하고 프레임을 구성하는 이미지의 너비와 높이 그리고 프레임의 수는 Filter 크기와 Padding 여부에 따라 변화됩니다.

Convolution 3D의 가중치는 (3, 3, 3, 3, 16)의 형태이며, 이는 (3, 3, 3, 3) 크기의 Filter가 16개 존재한다는 의미로 해석할 수 있습니다. (3, 3, 3, 3) Filter는 프레임, 너비, 높이, RGB 채널을 의미합니다.

이렇게 Stride, Padding, Zero Padding, Convolution 1D/2D/3D에 대해 실제 코드를 통한 내용까지 확인해보았으며, 애매하게 이해되던 연산 과정 또한 조금 더 깊게 이해할 수 있게되었습니다!

마치며

다양한 차원의 Convolution은 단순하게 차원이 늘어나는 것만 아니라, 연산 방식이나 주로 사용되는 데이터 등이 바뀌기 때문에 처음 접하는 경우 이해하기 어려울 수도 있습니다.

검색을 통해 확인할 수 있는 다양한 정보를 기반으로 이해하는 것보다, 실제 가중치의 생김새, 연산 과정에서 어떠한 정보가 추출되고 압축되는지 등을 본다면 더욱 빠르게 이해할 수 있을 것 같아 코드 리뷰를 포함한 글을 작성하게 되었습니다.

궁금증을 갖고 제 포스트를 읽어주신분들께서, 원하는 대답을 얻어가셨으면 좋겠습니다.

긴 글 읽어주셔서 감사합니다.