문제 풀면서 중요한 포인트라고 생각되어 기억하고 싶은 부분들

7576 토마토 문제

배열을 이용한 큐 구현

write pointer와 read pointer로 간단하게 큐를 구현할 수 있음

push시 write pointer 하나 증가시키고, pop시 read pointer 하나 증가 시킴

write pointer와 read pointer가 같은 인덱스 위치에 오게 된다면 큐에 들어왔던 원소를 전부 읽어내어 빈 상태의 큐가 된 것

메모리 효율성을 생각한다면 원형 큐로 구현하는 것도 좋아보임

헤당 풀이에서는 BFS를 구현하기 위해 Tomato 구조체의 day 필드, 큐, 안익은 토마토의 개수를 저장하는 변수 unripe를 이용하고 있음

int write = 0;  // write pointer
int read = 0;   // read pointer

typedef struct
{
    int x;
    int y;
    int day;
} Tomato;

// 객체 배열
Tomato queue[MAX * MAX + 5];

// 배열로 큐 구현
void push(int x, int y, int day)
{
    if (write >= MAX * MAX + 5)
    {
        printf("Queue overflow.\n");
        return;
    }
    queue[write].x = x;
    queue[write].y = y;
    queue[write].day = day;
    write++;
}

Tomato pop(void)
{
    return queue[read++];
}

int isEmpty(void)
{
    return write == read; // true면 1, false면 0
}

2차원 배열에서 for문을 통한 상하좌우 이동

정수배열 dx와 dy를 정의하여 2차원 배열에서 위, 아래, 좌, 우 원소들을 확인하는 네 번의 작업을 하나의 for문으로 구현할 수 있음

	// 토마토 익히기
    int dx[] = {-1, 0, 1, 0}; // 좌우 이동
    int dy[] = {0, 1, 0, -1}; // 상하 이동
    while (!isEmpty())
    {
        Tomato current = pop();
        // 위 아래 양 옆 확인
        for (int i = 0; i < 4; i++)
        {
            int checkX = current.x + dx[i];
            int checkY = current.y + dy[i];

            // 배열 범위 안인지 체크
            if (checkX < 0 || checkX >= n || checkY < 0 || checkY >= m)
                continue;
            // 안익은 토마토 익히고 큐에 넣기
            if (box[checkX][checkY] == 0)
            {
                box[checkX][checkY] = 1;
                unripe--;
                push(checkX, checkY, current.day + 1);
            }
        }
        // 토마토 다 익음!
        if (unripe == 0)
        {
            printf("%d", current.day + 1);
            return 0;
        }
    }

11729 하노이 탑 이동 순서

웰노운 문제지만 나는 처음 시도해봤던 터라 규칙을 찾는데 약 1시간이 넘게 걸렸음 (요즘 머리가 잘 안돌아간다.. ㅠ)

처음엔 스택으로 구현해야되나 싶었는데 규칙이 눈에 보이고 나니 굳이? 싶었음

계속 그림을 그리고 프로세스를 따라가다 보니 최종단계와 직전단계 사이의 연관성이 보이기 시작했음

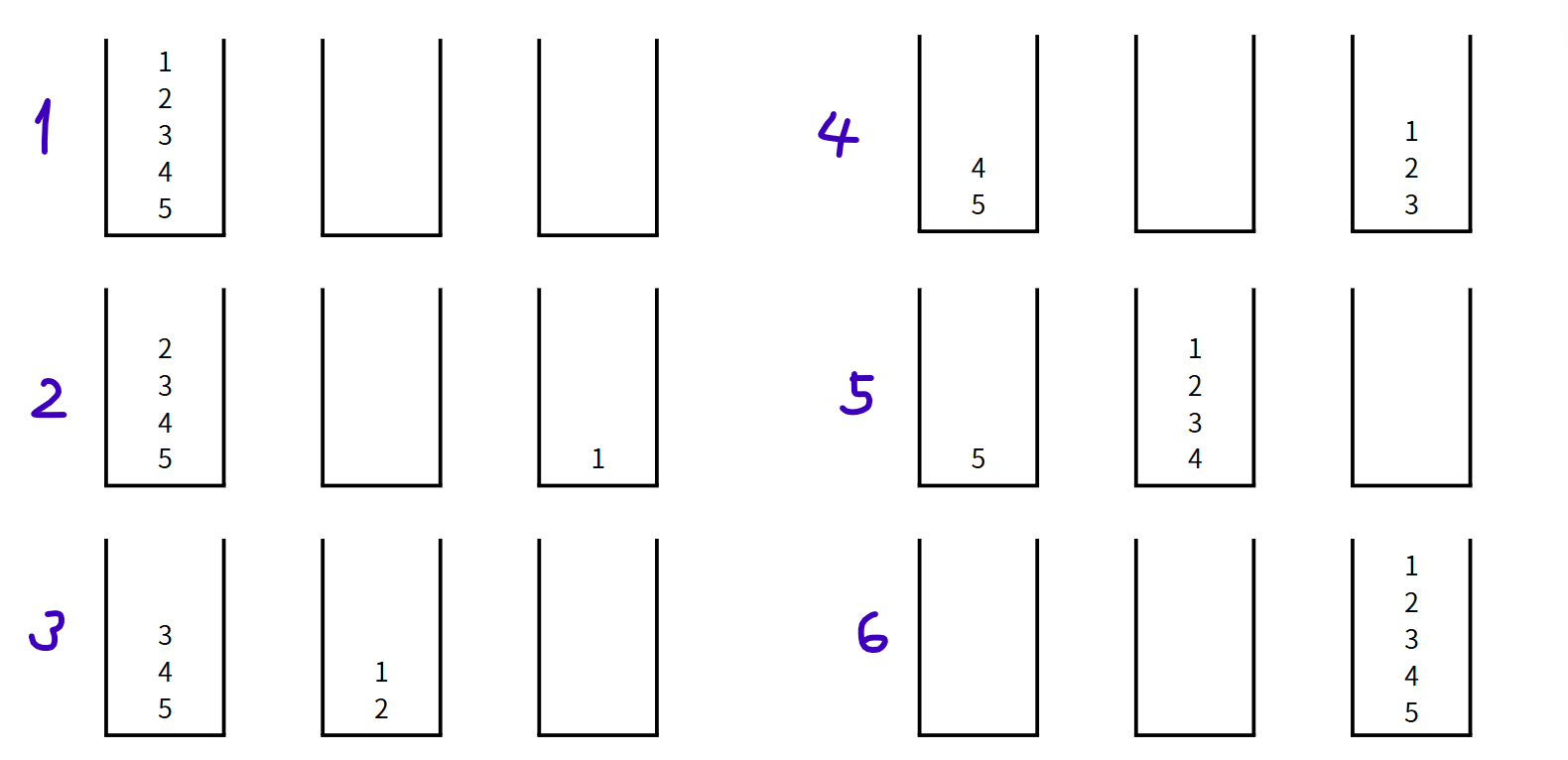
찾아낸 규칙을 일반화시키는 과정도 조금 애를 먹었지만 해냄

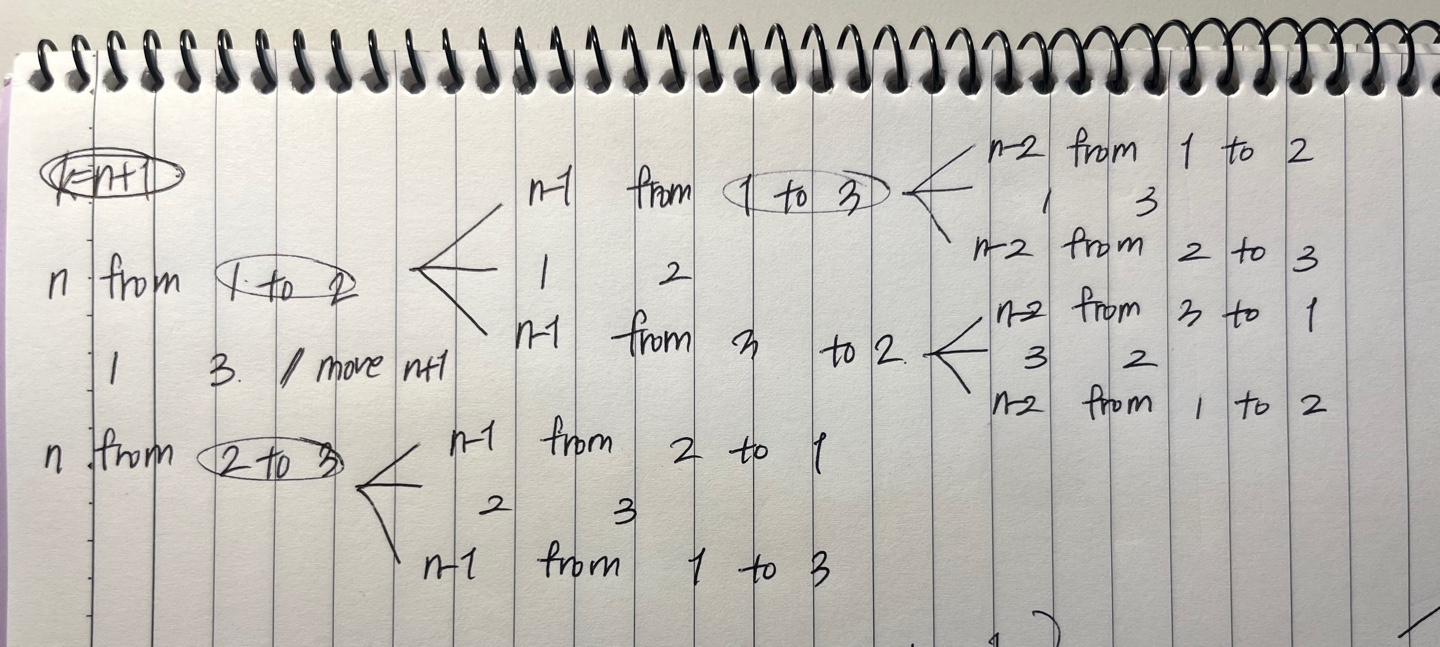
저번 학기 알고리즘 수업 때 재귀 함수를 많이 다뤄봤던게 코드 구현에 크게 도움이 됨

정수배열로 집합 구현

집합을 구현하고 싶었던 이유는

n from __ to __

빈칸에 1, 2, 3 중 두 수가 들어가는데 들어가지 않은 나머지 하나의 수를 알아내고 싶었기 때문 (나중에 알게되었는데 하노이 탑 문제에서는 이걸 보조(auxiliary)기둥이라고 부른다고 함)

간단한 정수배열에 for문으로 인덱스를 확인하는 방법으로 해결

// base N from A to B function
void fromTo(int n, int from, int to)
{
    if (n == 1)
    {
        printf("%d %d\n", from, to);
        return;
    }
    int aux; // 보조기둥
    int set[] = {1, 2, 3};

    for (int i = 0; i < 3; i++)
    {
        if (set[i] != from && set[i] != to)
        {
            aux = set[i];
            break;
        }
    }
    fromTo(n - 1, from, aux);
    printf("%d %d\n", from, to);
    fromTo(n - 1, aux, to);
}