12865 0-1 KnapSack (day 3)
2차원 배열을 이용한 풀이
item이 N개이고 최대 무게가 K일 때 [N+1][K+1] 크기의 2차원 배열을 그려서 품.
item i를 고려하며 최대 무게 j까지 허용할 때 [ WITH i UNDER j ] (0<i<=N, 0<j<=K)
if ( item i의 무게가 허용된 무게 j보다 무거울 경우) i-1단계 값이 그대로 내려옴
if (weight[i-1]>j) table[i][j] = table[i-1][j];
else 최적해는 반드시 다음 두 경우 중 하나 (더 큰 값 고르면 됨)
- item i가 포함됨 -> [ WITH i-1 UNDER j-(item i 무게) ] + (item i의 가치)
- item i가 포함되지 않음 -> [ WITH i-1 UNDER j ]
else table[i][j] = max(value[i-1]+table[i-1][j-weight[i-1]], table[i-1][j]);

최적해를 한칸씩 채워나가며 배열이 다 채워졌을 때 제일 마지막 칸이 문제의 정답.
코드 구현시 주의할 점은 직전 단계 결과를 참조하기 때문에 시작 전에 배열의 1행과 1열을 0으로 초기화 해줘야 한다는 점.
(사실 위의 풀이는 Dynamic Programming보단 Memorization 기법에 가깝지 않나 싶음)
1차원 배열을 이용한 풀이
사실 [N+1][K+1] 크기의 2차원 배열은 사치.
배열을 초기화하는 것과 마지막 단계의 값이 정답이 된다는 점은 동일하지만 [K+1] 크기의 1차원 배열 단 두 줄만 있으면 위의 문제를 해결할 수 있음 (이전 단계를 전부 참조하는 것이 아니라 직전 단계만 참조하기 때문)

두 배열이 서로의 값을 긴밀하게 주고 받음
bool a = true; // (배열 구분해주는) 스위치 역할
int b;
for (int i = 1; i < N + 1; i++)
{
// 스위치에 의해 결정되는 배열 행 인덱스
if (a == true)
b = 1;
else
b = 0;
for (int j = 1; j < K + 1; j++)
{
if (weight[i-1] > j)
table[b][j] = table[!b][j];
else
table[b][j] = max(value[i - 1] + table[!b][j - weight[i - 1]], table[!b][j]);
}
a = !a;
}
printf("%d", table[b][K]);
2차원 배열을 사용했을 때와 1차원 배열을 사용했을 때의 엄청난 메모리 사용량 차이가 보임.
우리 모두 가급적 효율적으로 살자
2447 재귀 별찍기 (day 4)
입력값이 n일 때 n/3에 대하여 재귀적으로 함수를 호출한다는 것은 알기 쉬운 포인트.
공백의 규칙이 각 단계의 n과 관련된 재귀적인 특성을 띈다는 점을 명심할 것.
10026 재귀 별찍기 (day 5)
Stack을 이용한 DFS 구현하여 Queue를 이용한 BFS 문제(토마토 문제)와 비슷하게 품.
배열로 stack 구현
pointer 2개(write pointer와 read pointer)를 사용하여 구현했던 queue와는 다르게 LIFO 구조인 stack은 pointer 1개로 구현 가능.
단 전위/후위 연산자 잘 구분하여 쓸 것.
- 전위 증가/감소 연산자 : 변수의 값을 1 증가/감소시킨 후 반환
++p --p
- 후위 증가/감소 연산자 : 변수의 값을 반환 후 1 증가/감소
p++ p--
stack의 경우
push시
pointer++;
pop시
--pointer;getchar()
표준 입력 버퍼에서 한 개의 문자를 가져오는 '표준 입력 함수'
getchar(); // (단독으로 써서)버퍼에 남아있는 '\n'(개행문자) 제거자 이제 본론으로
먼저 정상인이 보는 구역을 구함
- 처음 등장하는 문자(R,G,B 중 하나)를 stack에 push
- pop -> 해당 좌표의 상하좌우를 탐색하며 같은 문자를 stack에 push
- 이 때 방문한 좌표는 그 값을 바꾸어 visited됨을 표시 (후에 색맹이 보는 구역을 구하기 위해 R과 G를 하나의 문자로 표시)
- stack이 채워졌다가 비워지는 횟수는 = 구역의 개수
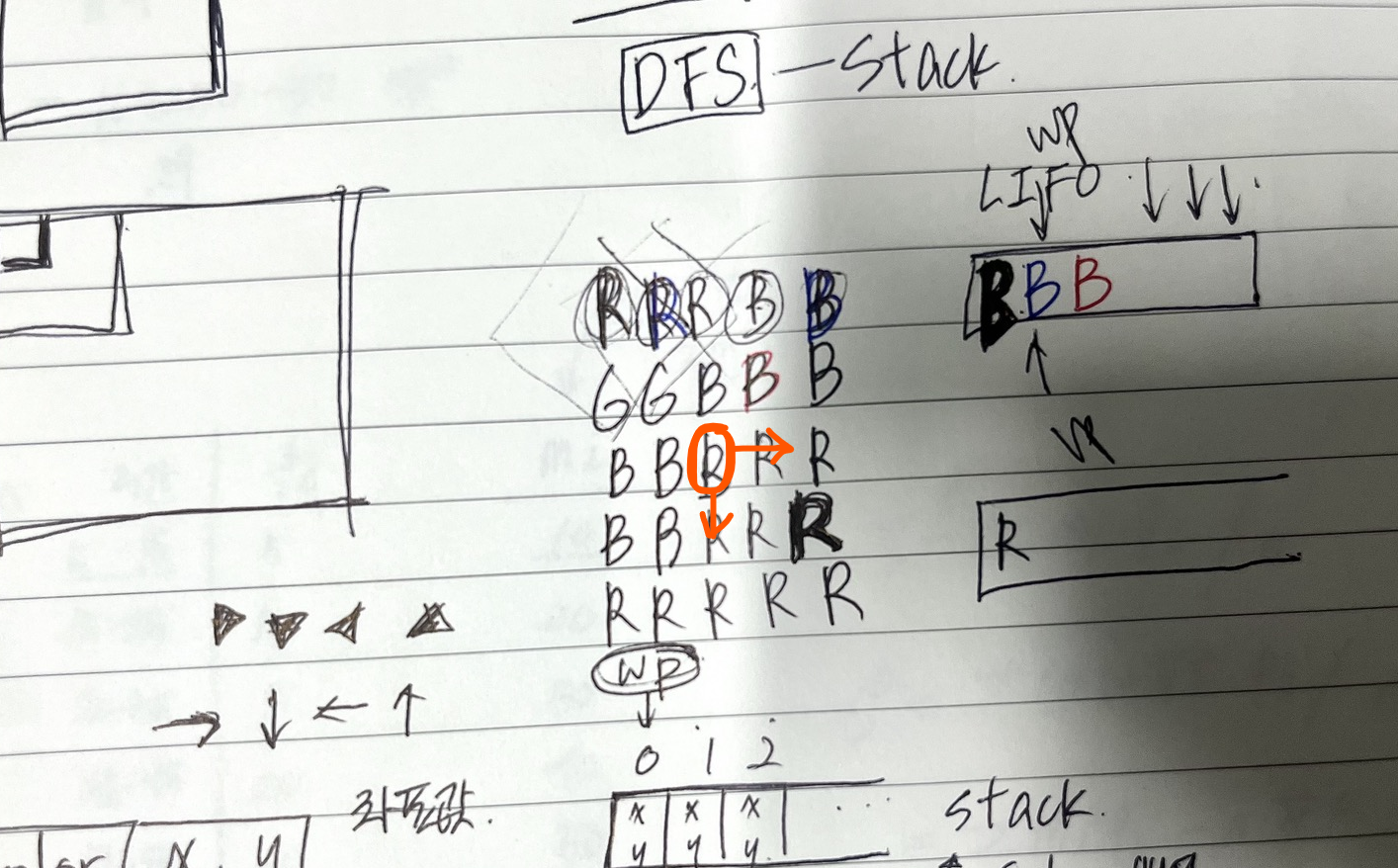
// 우, 하, 좌, 상 순으로 탐색하며 자신과 같은 문자 check
int dx[] = {1, 0, -1, 0};
int dy[] = {0, -1, 0, 1};
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
{
if (rgb[i][j] == '0' || rgb[i][j] == '1')
continue; // 이미 방문한 좌표 건너뛰기
char current = rgb[i][j]; // 현재 탐색 중인 문자
push(i, j);
while (!isEmpty())
{
Color c = pop();
switch (rgb[c.x][c.y])
{
case 'R':
case 'G':
rgb[c.x][c.y] = '0';
break;
case 'B':
rgb[c.x][c.y] = '1';
break;
} // 방문 표시
for (int k = 0; k < 4; k++)
{
int newX = c.x + dx[k];
int newY = c.y + dy[k];
if (newX < 0 || newX >= n || newY < 0 || newY >= n)
continue; // 범위 안인지 체크
if (rgb[newX][newY] == current)
push(newX, newY);
}
}
normal++;
}
}
이제 같은 로직으로 1과 0을 구분하여 색맹이 보는 구역의 수를 구하면 됨.
