Cost Function

비용함수란 간단히 말하자면 실제와 예측 결과의 다른 정도를 구하는 함수다.
비용함수를 통해서 원래의 값과의 오차를 계산한 뒤,
그를 근거로 가설함수를 더 개선하는 것이다.

우리는 보통 가설함수의 매개변수를 최적화해서 가장 오차가 작은 가설함수를 만드는 것이 최종적인 목표이다.
비용함수를 통해 얻은 오차는 음수가 될 수도 있기 때문에 보통 제곱을 해준 뒤 모든 경우에서의 오차제곱을 더해서 이전과 비교해준다.
오차의 제곱합이든, 제곱의 평균이든 기준이 되는 값이 최소가 되도록 만드는 것이 optimize이다.

Gradient Descent Method

경사하강법은 앞서 말한 오차의 최소가 되는 지점을 찾는 optimizing 기법중 하나이다.

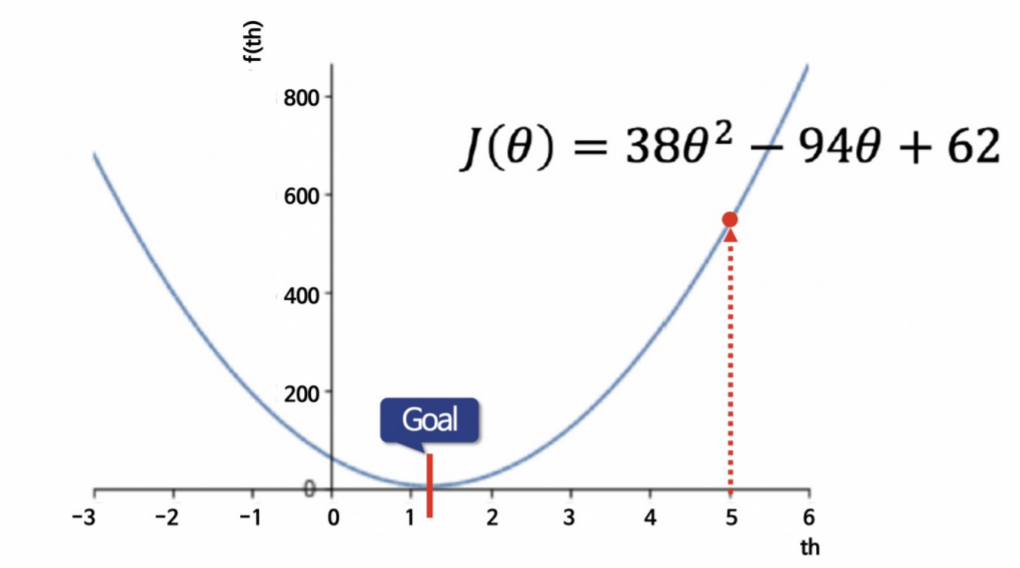
이러한 그래프에서 랜덤한 지점을 선택한 후,
cost function을 미분한 값에 learning rate를 곱해준 값을
기존의 $x$ 값에서 빼주어 이동한다.

Learning rate

학습률이라고 부르며, 모델이 학습하는 정도를 지정해줄 수 있는 Hyper Parameter이다.
큰 값을 지정해주면 빠르게 이동할 수 있지만 도착지에 도착을 못할수도 있다.
함수의 하단으로 갈수록 진동만한다.
하지만 너무 작은 값을 주면 언젠간 도착할 수 있겠지만 매우 느리기 때문에 좋지 않다.

GDM의 단점

GDM의 치명적인 단점은 바로 지역해의 유무이다.
우리가 찾는 도착지는 바로 전역해이다.
함수 전체에서 가장 작은 값인데 GDM은 전역해를 찾던 도중에 지역해를 만나면 변화량이 줄어드는것을 보고 전역해라고 착각해서 멈출 수 있다.

또한 GDM을 사용하기 위해선 Covex(볼록)함수라는 점이 필수적이다.

SSE, MSE, RMSE

앞서 말했던 오차의 관한 이야기이다.
오차는 실제값에서 예측값을 빼준 값이다.
그렇기 때문에 오차는 당연하게도 양수도, 음수도 나올 수 있다.
그렇기 때문에 오차를 제곱을 한 뒤에 사용하는것이 일반적이다.

SSE

SSE는 sum square error의 줄임말로, 말 그대로 오차의 제곱을 더한 수치이다.

MSE

Mean square error의 줄임말로, 오차 제곱의 합이 아닌, 오차 제곱의 평균을 보는 방법이다.
이 방법은 데이터셋이 클수록 연산량이 많기 때문에 속도가 느려질 수 있다.

RMSE

그렇기 때문에 root mean square error를 사용하여 수치값을 줄여서 사용한다.
mse에 root한 값이다.

선형회귀모형에 사용되는 a와 b를 조정하여 이러한 오차들의 최소값을 찾는것이 목적이다.