Soft Actor-Critic: Off-Policy Maximum Entropy Deep Reinforcement Learning with a Stochastic Actor
https://arxiv.org/abs/1801.01290
Soft Actor-Critic(SAC)는 Policy Gradients 모델들 중 TRPO, PPO와 더불어 가장 유명한 모델인듯 하다.
비교적 최근의 모델인 만큼 성능도 더 좋지 않을까 기대해본다.
1. Introduction
이 논문에서는 offpolicy maximum entropy actor-critic algorithm인 soft actor-critic (SAC)를 제시한다.
Off-Policy learning을 이용하여 표본 효율성과, maximum entropy를 이용하여 탐험과 안정성을 챙겼다고 한다.
(entropy가 높을수록 무작위적이라는 뜻이며, 탐험을 장려한다고 볼 수 있다.)
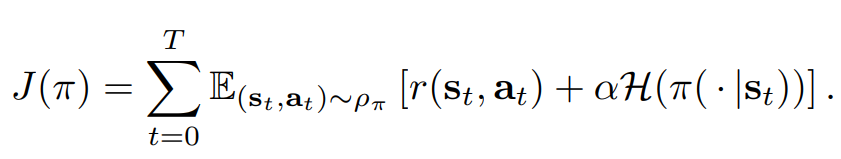
(H가 엔트로피를 의미, J가 최대화 해야하는 objective)
4. From Soft Policy Iteration to Soft Actor-Critic
4.1. Derivation of Soft Policy Iteration
먼저 tabular setting에서 유도한 뒤, 이를 continuous setting으로 일반화 한다.
정책 평가
고정된 정책에 대해, 정책 평가를 통해 soft Q-value를 계산할 수 있다.
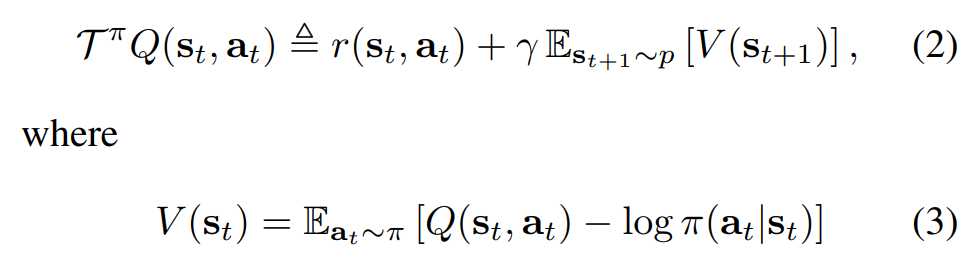
엔트로피가 추가됨으로 인해 해석이 복잡해졌다.
먼저 -log()의 형태가 엔트로피이며, - 기호가 있음에도 엔트로피가 더해진것이라는 점을 명심해야 이해하기 쉽다.
연쇄적으로 대입하면 매 타임스탭마다의 보상과 엔트로피의 총합이 되는것을 확인할 수 있다.
Q는 첫번째 행동이 결정되어 있으므로 첫번째 타임스탭에 엔트로피가 없다.
정책 향상
정책 평가를 했으니 정책 향상을 할 차례이다.
∏중에서 Q함수에 exp()함수와 정규화를 적용한 분포와 KL Divergence가장 작은 녀석으로 업데이트 한다.
KL Divergence가 작을수록 분포가 비슷하다고 보면 된다.
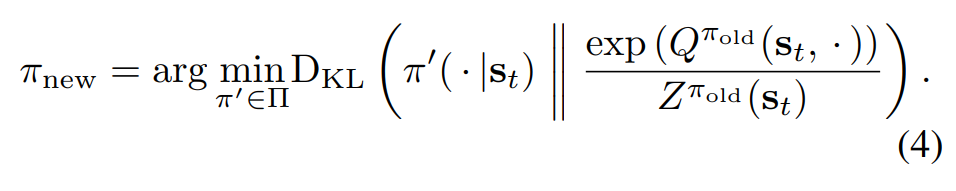
∏는 가우시안 분포 같이 매개 변수화 할 수 있는 정책들의 집합이라고 한다.
이때 tabular setting이다 보니 상태-행동 쌍을 일일이 지정하는 정책이 가능하다.
이를 continuous setting으로 일반화하면 문제가 생길수 있으니, 배제하는듯 싶다.
z는 Partition function으로 정규화를 시켜주는 녀석이라고 한다.
https://en.wikipedia.org/wiki/Partition_function_(statistical_mechanics).
(잘 모름 코드 분석때 알아보겠음..)
무한히 반복하다 보면 soft Q-value 기준 최적 정책으로 수렴이 보장된다고 한다.
하지만 soft Q-value를 사용하는 이유는 안정성과 탐험 등의 이유이기 때문에
절대적으로 좋은 성능은 보장 못하지 않을까 싶다.
soft Q-value가 기준이 아니라 Q-value 혹은 V-value 기준으로 해야 진정한 최적 정책이라고 생각하며,
그렇게 할 시 더 좋은 정책(ex.결정론적 정책)이 분명히 존재한다고 생각한다.
하지만, 어차피 근사적 해법을 사용하는 순간부터 최적 정책을 찾는것은 불가능 하며, 학습 효율을 고려해야 하기 때문에 이렇게 하는듯 하다.
4.2. Soft Actor-Critic
이제 continuous setting으로 일반화할 차례이다.

V, Q, π를 근사하게 된다. (가중치 ψ, θ, φ)
π로 표본을 추출하며 replay memory에 표본을 저장한다.
표본을 통해 V와 Q를 근사하고,
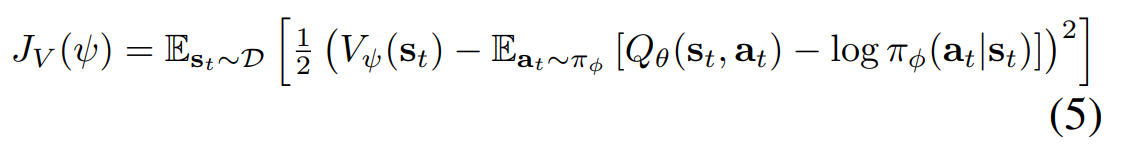
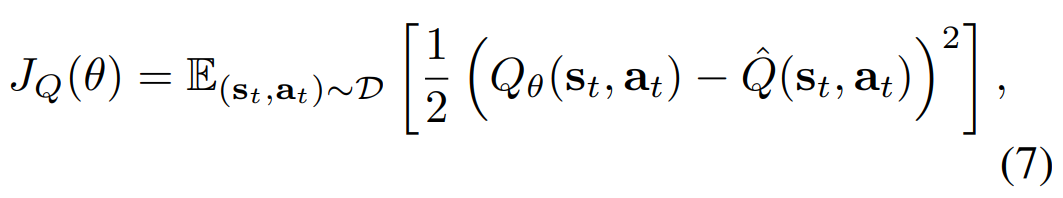
Q를 이용해 π를 업데이트 하게 된다.
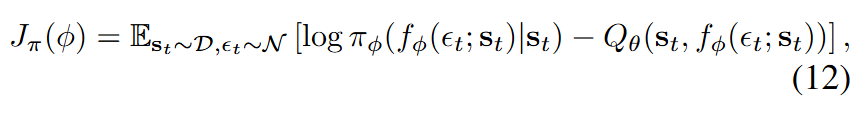
log_prob - Q값을 최소화하여 성능을 향상시키게 된다.
Q값을 늘리는 방향으로 정책의 가중치를 수정하면 성능이 좋아질것이다.
동시에 행동의 엔트로피를 늘리도록 항이 추가되어있다. 따라서 탐험을 장려할것이다.
위 discrete할때의 objective가 갑자기 변하게되는 수학적 전개는 잘 모르겠다.
최종 objective가 너무 직관적이며, 간단하다.
아무리 생각해도 잘 되니까 있어보이기 위해서 분석해서 논문에 추가한거같다
혹은 왜 되는지 분석정도로 생각된다.
사실 Q만 근사하면 되나, V를 같이 이용하면 안정성, 다른곳에서의 쓸모 등에서 유용해서 그렇게 했다고 하며,
Q 네트워크도 2개를 독립적으로 학습시켜서 같이 사용한다고 한다.
(Double DQN과 유사한 원리이지 않을까 싶음)
5. Experiments ~
보상의 스케일에 따라 성능이 달라진다고 한다.
정책은 Q함수에 exp()함수와 정규화를 적용한 함수와 비슷해지도록 업데이트 된다.
이는 소프트맥스 함수와 비슷해 보이는데, 소프트맥스 함수는 비율보단 값들의 차이가 중요하다.
예를들어 소프트맥스 함수에 [1,2,3]과 [10,20,30]을 넣게 되면
tensor([0.0900, 0.2447, 0.6652])
tensor([2.0611e-09, 4.5398e-05, 9.9995e-01])
로 후자가 훨씬 결정론적인 확률을 반환함을 확인할 수 있으며, 따라서 보상의 스케일에 따라 결과가 다름은 당연하다.
Experiments관련 내용을 직접 구현해보며 내 경험을 포함해서 다음 벨로그때 정리해 보겠다.