미리 알아야 하는 지식 - 몬테카를로, 시간차 학습
n단계 시간차학습(n-step TD)
몬테카를로 방법은 표본을 생성하고 이득을 측정, 가치함수 업데이트를 반복한다.
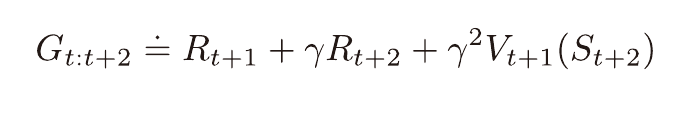
TD방법은 표본과, 다른 가치함수의 추정값을 이용(부트스트랩)하여 가치함수를 업데이트한다.
여기서 표본을 몇개 사용하느냐에 따라서 n단계 시간차 학습이라 부른다.
몬테카를로와 다르게 시간차학습은 에피소드가 끝날때까지 기다릴 필요가 없으며,
n이 커짐에 따라 몬테카를로 방법이 될 수 있다. (일반화)
또한 가치함수 업데이트 방식이 다른만큼 위 방법이 유리한 상황이 다수 존재한다.
n단계 살사
살사 방법은 on-policy 방법으로 입실론 탐욕적인 정책π를 이용하여 학습을 하는 방식이다.
n단계 살사는 기존 살사에서 표본을 n개 사용하는 것과 같다.
n단계 off-policy 살사(Q-Learning)
위 n단계 살사 방식의 off-policy버전이다.
off-policy는 on-policy를 포함한다.
off-policy방식이니 목표정책 π를 가치함수에 탐욕적이도록 해줄 수 있다.
행동정책 b를 사용하니 이득에 중요도추출비율을 곱해줘야 한다.
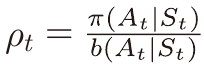
아래 식에 단순히 중요도추출비율을 곱하면 분산이 커진다는 단점이 있다.
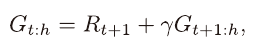
이를 보완한 식으로 아래와 같이 표현이 가능하다.
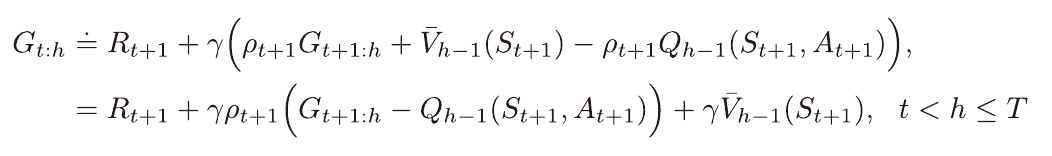
(추가된 부분을 제어변수라고 하며 총 기댓값에는 영향을 못 끼친다.)
π와 b가 같을시에는 중요도 추출비율이 1이 되며, 살사방식과 같아진다.
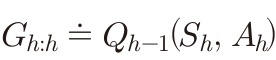
n단계 트리 보강 알고리즘
이 방법은 중요도 추출비율을 사용하지 않는 off-policy 방법이다.
하나의 시간단계에서 행동들의 π에서 확률을 가중치로 사용하여
표본과 다른 가치함수의 추정값을 같이 이용해주는 방법이다.
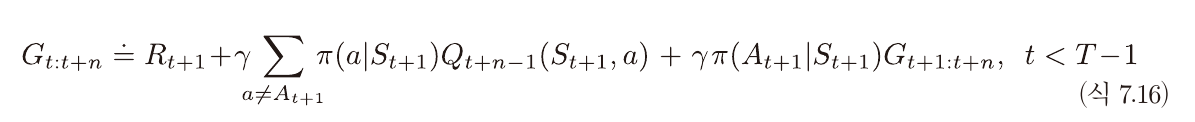
위와 같이 재귀적으로 표현이 가능하다.
n단계 Q(σ)
이 방법은 시간차학습부터 몬테카를로,
on-policy, off-policy, n단계 트리 보강 알고리즘까지
모두 일반화 시킨 방법이다.

n에 따라 사용하는 표본의 수가 달라지며,
π와 b가 같다면 중요도추출비율은 항상 1이 된다.
또한 σ가 0일때는 트리 보강 알고리즘(가중치)을, 1일때는 중요도추출비율을 사용하는 방식이며 0과 1사이의 연속적인 값 또한 가능하다.
트리 보강 알고리즘의 이득은 다음과 같이 변형 가능하다.

아래는 중요도추출비율을 사용한 이득이며 두개가 유사함을 이용한 알고리즘이다.
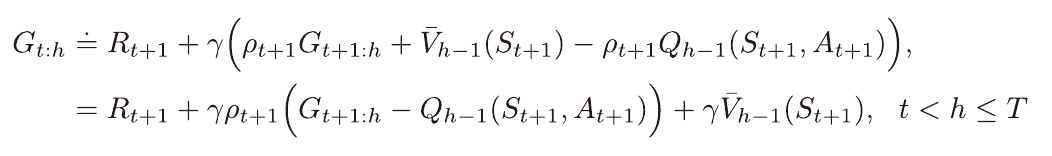
σ값에 따라서 G-Q부분에 곱해지는 값이 달라지고
이에 따라 V가 다 지워진다면 -> 중요도추출비율,
아니면 트리 보강 알고리즘이 되는 느낌으로 이해하면 되겠다. (정확한 설명 아님)
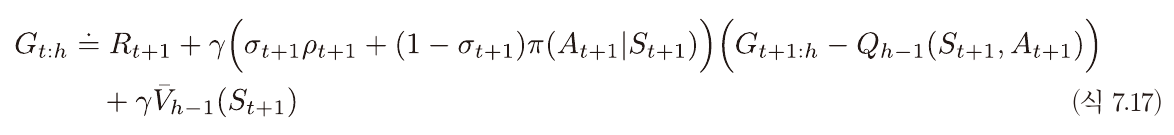

번외
계산량이 매우 적은 퍼즐과 같은것들은 위 알고리즘으로 해결 가능하다.
하지만 매우 많은 경우의수(ex 이미지)를 다뤄야 할때는 해결이 불가능하다.
인공신경망을 이용하여 근사적으로 측정하는 방법을 앞으로 공부하게 될 것 같다.
그전에 위 알고리즘을 실제로 구현해봄으로써 기초 개념을 탄탄하게 만들어야겠다.
뭔가를 만들고 자랑스럽다면 링크를 올려야겠다.
