SVM loss로 Weight를 구해도 bug가 존재한다?!
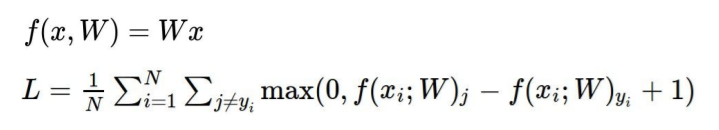
<SVM loss 구하는 공식>
SVM loss를 사용하여 Loss=0 인 Weight 값을 구했다면 과연 Loss=0일 때 Weight 값이 유일한 값일까?!
만약! Loss=0일 때 을 한다면 Loss 값은?!
.png)
loss=0인 car를 이용하여 알아보자!
weight를 제곱하지 않았을 때 loss는?
.png)
했을 때 loss는?
.png)
즉, weight 를 제곱하여 구한 Loss의 값 또한 0으로 나오기 떄문에 해당 Weight의 값은 유일한 값이라고 할 수 없다!
유일하지 못한 Weight 값을 활용한다면?! 과적합을 불러온다?!!
💡 과적합(OverFitting)이란? train data에만 지나치게 적응되어 그 외의 데이터에는 제대로 대응하지 못하는 상태를 말함..png)
<과대적합된 경우>
모델이 과적합되면 훈련 데이터에 대한 정확도는 높을지라도, 새로운 데이터. 즉, 검증 데이터나 테스트 데이터에 대해서는 제대로 동작하지 않는 문제가 있다.
모델 학습이 과적합된 경우에는 학습 데이터에서 불필요한 요소 (noise)까지 학습한 상태로 볼 수 있다.
과대적합은 막고! test data에도 잘 동작하게 하기 위해서는 어떻게 해야할까?!
.png)
<우리가 하고 싶은 최종 예측 모양>
사각형이 test 데이터를 뜻함.
Regularization을 사용하면 된다!
regularization을 직역하면 정규화로 번역되지만 일반화라고 번역하는 것이 더 적합하다.
regularization을 활용하여 model이 train data에 overfitting (과대적합)되는 것을 방지하여 test data를 적용하면 좋은 결과를 얻을 수 있다.
💡 즉, unique한 weight 값을 결정하기 위해서 regularization이 생긴 것이다. regularization를 활용하여 weight가 얼마나 괜찮은지 측정할 수 있다. (data loss 부분은 train data에 일반화, regulatization은 test에 일반화하려는 것)- regularization을 사용하면 train data에 대한 loss 값을 커진다?!
→ 데이터에 대한 정확도는 안좋아지지만 test set에 대한 퍼포먼스는 좋아지는 것을 뜻함
→ regularization 에서는 weight = 0 이 가장 좋은 것
하지만 data loss는 분류를 해야 하기 때문에 weight ≠0 이 될수는 없다.
즉, dats loss와 regularization loss와 싸우면서 data set에도 fit하고 가장 최적화된weight를 구함
(a way of trading off training loss and generalization loss on test set)
.png)
<SVM loss에 regularization을 적용한 식>
.png)
regularization strength로 하나의 hyperparameter를 뜻한다.
Regularization 종류
.png)
regularization은 위의 이미지를 봐도 많이 있지만 L2 regularization이 가장 많이 사용된다.
L2 Regulatization을 사용해서 Bug를 박멸하자!
x=[1,1,1,1]일 때 w1을 활용한 data loss = 1, w2일 때는 data loss= 1로 같은 결과값을 가진다.
그러면, regulatization에서는 어떤 weight를 선호할까?
regularization은 weight가 특정 값만 영향을 주는 것보다 모든 원소값에 영향을 주는 것(diffuse over everything)을 선호하기 때문에 w1보다 w2를 더 선호한다.
Regularization을 진행하면 overfitting은 DOWN!
test data에 대한 일반화 성능은 UP!
원본 사이트
https://leather-pedestrian-89b.notion.site/Regularization-85f701af9726443b8217739b1e7508a2
