Deep Fuzzy Clustering—A Representation Learning Approach 정리

Abstract

Fuzzy Clustering은 다양한 클러스터링 방법론 중 전통적인 soft clustering 접근법이다.
하지만 high dimensional data에 대해서 한계점이 분명하기 때문에 논문은 deep neural network를 통해 feature space에 나타난 representation data에 fuzzy clustering을 적용시킨 Deep Fuzzy Clustering을 제안한다.
표현학습에서 군집 친화적(clustering-friendly)으로 표현하기 위해 3가지 조건을 제시한다.

• 1. feature space에 나타난 representation 결과들은 reconstruction 에 효과적이어야 한다.
• 2. 클러스터링이 잘 되기 위해서 군집 내 압축성은 최소화, 군집 간 거리는 최대화해야 한다.
• 3. 동일 클래스의 거리는 가까워져야 하므로 데이터 간 유사성을 조정해야 한다.
     논문은 소프트 클러스터링과 표현학습을 동시에 수행하기 위해 graph-regularized deep normalized fuzzy compactness and separation clustering model 을 제안한다.

Introduction

고차원 데이터와 복잡한 잠재 분포를 다루는 데에 있어 전통적인 퍼지 클러스터링의 한계와 기존 방법들의 한계를 말한다.
제안된 방법은 딥 뉴럴 네트워크를 활용하여 클러스터링에 보다 효과적인 데이터 표현을 학습함으로써 이러한 한계를 극복하고자 한다.
표현 학습과 deep fuzzy clustering을 병합하기 위해 다음과 같은 3가지를 최적화하는 파라미터 튜닝을 목표로 한다.

• Auto Encoder의 재구성 오차
• 클래스 간 / 클래스 내 scatter-matrix KL divergence
• affinity의 일관성

논문은 다음과 같은 기여점을 가진다.

• 표현학습과 soft clustering을 동시 수행하기 위해, 처음으로 표현학습에 fuzzy clustering을 추가했음.
• 새로운 feature space에서 효율적으로 클러스터링하기 위해 새로운 FCS(Fuzzy Compactness and Separation)정규화 알고리즘을 제시함. 또한, fuzzifier m 이 클러스터링 성능에 얼마나 영향을 끼치는지 알기 위해 모든 데이터 셋에 대해서 실험해봄.
• 제안한 deep fuzzy clustering 모델 내에 hidden feature space의 regularization term 에 discriminative graph를 적용시킴. 그리고 클러스터링을 통해 pseudo-labeling을 수행해서 affinity를 계산함.
• deep fuzzy clustering의 optimization algorithm을 제안함. 그리고 real-world high-dimensional data에 대해 실험하여 baseline methods 와 성능을 비교함.

Related Work

• FCM Clustering

  object function
  
  $X = input\\c = cluster\;centers$
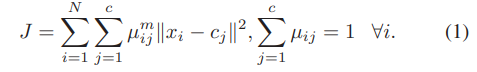
  $m>1$은 fuzzifier, $\mu_{ij}$는 $x_i$, $c_j$에 대한 fuzzy membership
  이 때, 멤버십 $\mu_{ij}$와 cluster center $c_j$는 다음 수식을 따른다.
  
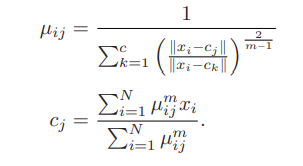
  FCM은 fuzzy membership, cluster center가 수렴할 때까지 업데이트 진행

• Deep AE

  
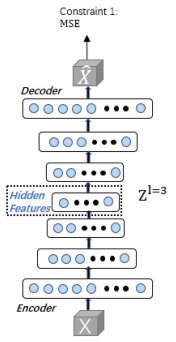
  AE는 data representation에서 unsupervised data에 대해 자주 쓰이는 모델이다.
  encoder와 decoder로 구성되며, encoder의 경우 데이터를 차원 축소하고, decoder의 경우 reconstruction을 통해 해당 feature들을 원본 데이터와 비슷하게 재구성한다.
  
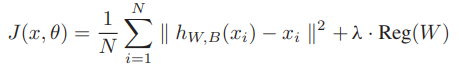
  위와 같은 목적함수를 가지며, 원본 데이터와 재구성 데이터 간의 오차를 최소화 시키는 것이 목적이다.
  $\lambda = Euclidean\;norm\\Reg(W) = regularization\;term$

• Deep Clustering Based on Student's-t Distribution

  DEC model, IDEC model은 AE와 clustering을 동시에 최적화하는 모델이다.
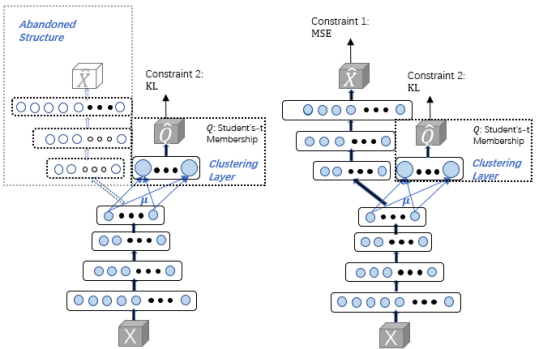  (왼: DEC model, 오: IDEC model)
  기존 AE와 비슷하게, input data $X$의 차원은 $d$, hidden feature layer에 차원 축소 된 data $Z$의 차원은 $c$ 이다.
  그리고 $z_i$에 대해서 클러스터링을 진행하는게 DEC, IDEC의 특징이다.
  더 자세히 살펴보면,
  $x_i$가 $j$ cluster에 속할 확률인 output $q_{ij}$은 다음과 같은 수식을 따른다.
  
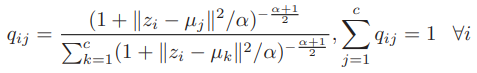
  $\mu$는 clustering layer(차원 $c$)의 trained weight이며, cluster의 center 값이고, 클래스의 개수는 $c$개이다. ($\alpha$는 하이퍼파라미터이고 보통 1로 세팅)
  
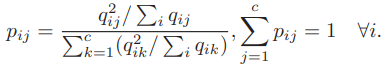
  target $p_{ij}$는 $q_{ij}$의 분산을 증가시키고, j번째 센터에 대해 정규화시킨 값이다.
  
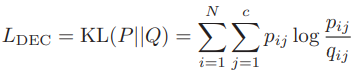
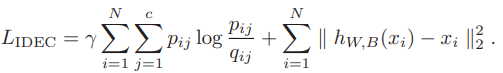
  DEC model의 loss는 $p_{ij}$와 $q_{ij}$의 KL divergence를 최소화하는 것
  IDEC model의 loss는 DEC와 유사하지만 KL divergence의 scale을 조절할 수 있는 $\gamma$ 상관계수가 있다.
  IDEC와 DEC의 차이는 모델 구조와 학습 과정의 loss값이다.

  • IDEC는 decoder 구조를 가져가고, MSE loss를 구하지만
  • DEC는 decoder와 MSE를 포기한 구조이다.
    DEC와 IDEC가 clustering에 용이하다고 하지만 representation 이전에 데이터 내적 가치를 고려하지 않았다.
    따라서 다음과 같이 graph-regularized deep normalized fuzzy compactness and separation(GrDNFCS) clustering model을 제안한다.
    

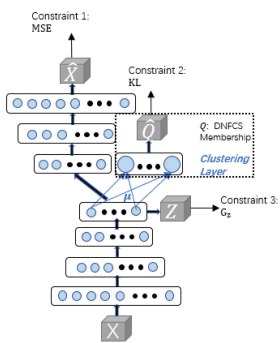
Pseudolabel-Based Affinity Graph-Regularized Deep Fuzzy Clustering Model

• A. Normalized FCS-Based Membership and KL-Divergence-Based Objective

  최근 FCM(Fussy C-Means)과 Student's-t distribution based approach를 포함한 다양한 clustering methods가 있지만 FCS는 fuzzy clustering method를 접목시켜 더 명확한 군집화를 이룰 수 있다.
  그리고 논문에서는 앞서 서술한 2번째 조건을 만족하도록 FCS를 Deep Normalization 시킨 DNFCS를 제안한다.
  1) Fuzzy Compactness and Separation (FCS)
  제안하는 내용 상, between-cluster scatter matrix / Within-cluster scatter matrix 두 가지 값이 도출된다.
  
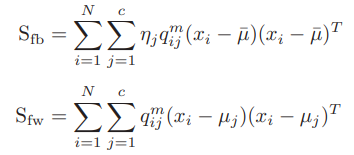
  $m$은 fuzzifier, $\mu_{j}$는 j번째 center의 representation, $\bar\mu$는 데이터 평균값이다.
  $S_{fb}$는 fuzzy between-cluster, $S_{fw}$는 fuzzy within-cluster score이다.
  이 때, 앞서 서술한 것처럼 군집 간 거리는 최대화, 군집 내 거리는 최소화 시켜야 하므로 Loss function은 $S_{fb}$를 최대화, $S_{fw}$를 최소화하는 조건식이어야 한다.
  
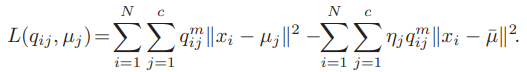
  $\eta_j$는 fuzzy membership $q_{ij}$를 $L(q_{ij},\mu_j)$에 대해 미분 가능하도록 하는 파라미터이다.
  FCS의 목적 함수에 따라서 $q_{ij}$는 다음과 같이 표현 가능하다.
  
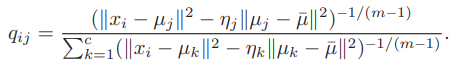
  2) Normalized FCS Membership
  앞서 보았던 기본 FCS 수식에서의 fuzzy membership($q_{ij}$)은 $\eta_j$나 $\frac 1{c(c-1)}$은 Loss function의 분자가 항상 양수임을 보장하지 않는다.
  positiveness를 보장하기 위해서 DNFCS가 제안된다.
  DEC와 IDEC에서 $z_i$가 input으로 들어가고, fuzzy membership이 output으로 나왔었다.
  그렇다면 위의 fuzzy membership 수식의 input을 다음과 같이 변형하여 나타낼 수 있다.
  
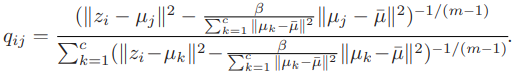
  $\beta$는 within-cluster / between-cluster distance를 조절하는 하이퍼파라미터이며 $q_{ij}$값이 positive하게 만드는 데 필수적이다.
  위와 같이 fuzzy membership을 나타낼 수 있으니 Loss function 또한 의미는 동일하지만 아래와 같이 변형 가능하다.
  
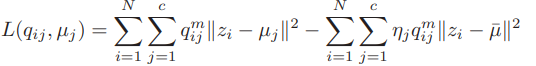
  위의 식을 보면, $\eta$가 나타내는 부분이 제곱 합 부분으로 바뀌면서($\beta$의 분모부분) 음수 값이 도출되는 것을 방지할 수 있게 됐다.
  within-distance를 $d_1$, between-distance를 $d_2$라고 했을 때, 학습 초기에 $d_1$의 스케일은 지나치게 높아졌다가 학습이 진행될수록 지속적으로 감소한다.
  하지만 $d_2$의 경우, 상대적으로 스케일이 큰 상태로 남아있을 수 있기 때문에 $d_1$에 효과적으로 영향을 미치기가 어렵다.
  때문에 정규화를 통해서 두 스케일을 동일하게 조정할 필요가 있었던 것이다.
  3) KL-Divergence-Based Objective Term
  처음 설정했던 목표 중에 KL-Divergence minimize가 있었다.
  fuzzy membership $q_{ij}$의 desire target인 $p_{ij}$이 있었고, $p_{ij}$에 $q_{ij}$를 근사시키는 수식은 다음과 같다.
  
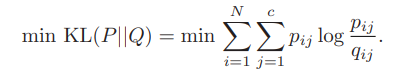
  이에 대해서 update를 위해 gradient를 구하면 다음과 같다.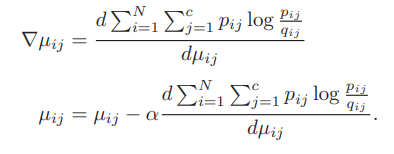
  이와 같이 gradient descent를 통해 KL-Divergence를 업데이트 하면 fuzzy membership의 분포가 j번째 클러스터에 더 명확히 밀집하게 된다.

• B. Analysis of Fuzzifier $m$

  fuzzifier $m$은 fuzzy membership의 softness를 조절하는데 굉장히 중요한 역할을 하는 하이퍼파라미터이다.
  
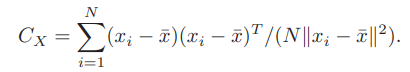
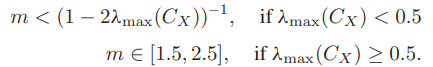
  $m$은 위와 같은 조건식을 통해 범위가 정해진다.
  $\lambda_{max}$는 $C_x$ matrix의 eigenvalue max 값을 뜻한다.

• Pseudolabel-Based Affinity Graph Regularization

  pseudo labeling을 통해 affinity를 regularization 하는 것은 처음 정한 3가지 목표 중 3번에 해당한다.
  representation set $Z$(new or encoded features)와 input dataset $X$의 관계에서 graph-based regularization은 다음과 같이 정의된다.
  
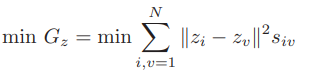
  여기서 $s_{iv}$는 $x_i$와 $x_v$간의 affinity score이다.
  즉, score가 높으면 $z_i$와 $z_v$의 distance는 작을 것이므로 regularization term이 minimize 된다. (그 반대의 경우면 regularization term도 반대로)
  전통적으로 affinity matrix는 KNN 알고리즘을 통해서 구했다.
  하지만 KNN의 경우 time-consuming이 굉장히 심한편이며 deep learning에 직접적으로 적용할 수가 없는 문제점이 있다.
  이를 해결하기 위해 논문에서는 clustering layer에서 예측한 fuzzy membership을 통해 pseudo-labeling을 진행하여 affinity를 계산하는 방법을 제안한다.
  뿐만 아니라, KNN-based보다 더욱 효율적이라는 장점도 있다.
  
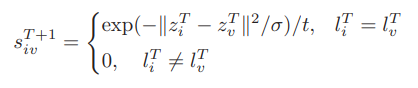
  전통적인 affinity-based approach에서는 모델 학습동안 affinity matrix를 업데이트할 수 없었다. 그러나 pseudolabel-based approach는 학습 과정동안 epoch가 1 이상이기만 하면 affinity가 업데이트가 가능하다.
  업데이트가 가능하므로 논문에서는 SGD를 통해 data에 shuffling trick을 주어 학습을 함으로써 모델 성능을 더 높였다.
  
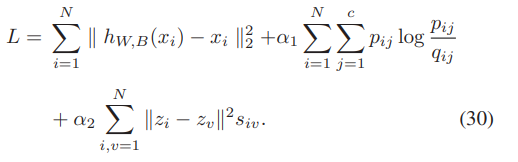
  앞서 설명되어왔던 deep fuzzy clustering model의 최종 loss function은 위의 수식과 같고, 논문에서는 이에 대해서 GrDNFCS fuzzy clustering이라고 명칭한다.

• Psudo-code
  

Experiments

논문에서는 MNIST, USPS, Reutersidf-10k, COIL20, Fashion-MNIST, STL-10으로 실험을 진행했다.

사용한 평가지표는 다음과 같다.

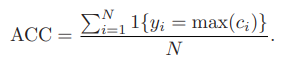
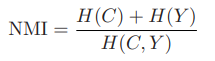
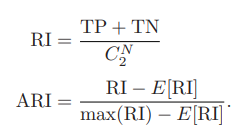
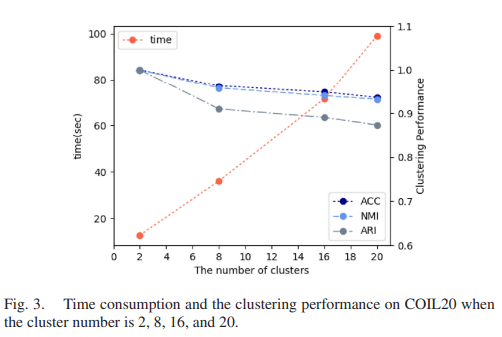
• time complexity analysis
  
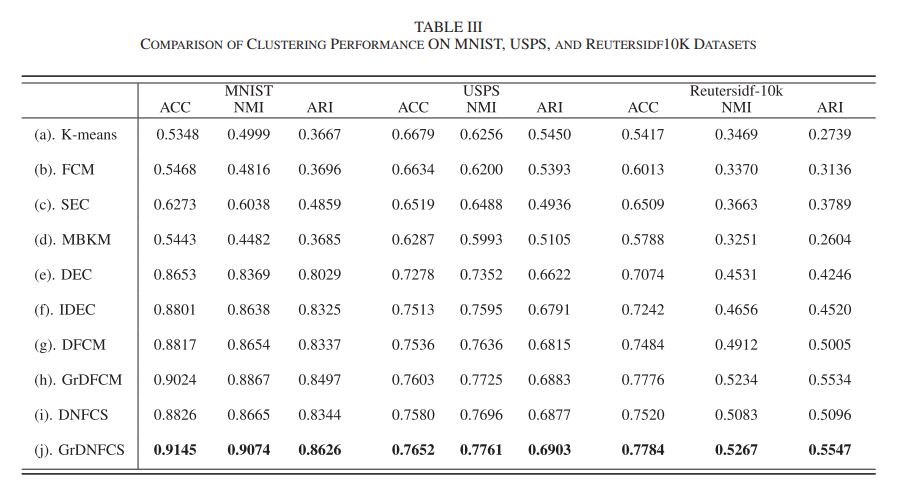
• performance
  

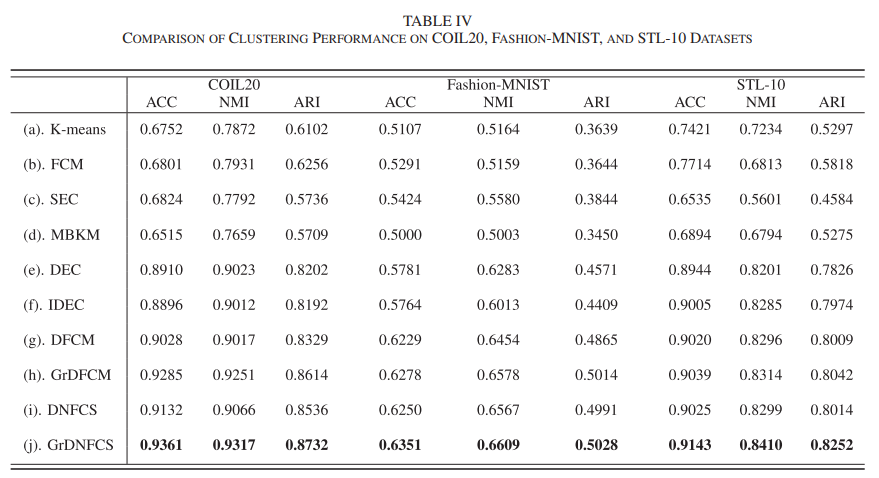
conclusion

제안된 GrDNFCS 모델의 성능과 특징에 대한 종합적인 평가를 제시했다.
실험 결과를 토대로 GrDNFCS 모델이 다른 클러스터링 알고리즘보다 우수한 성능을 보이며, 고차원 데이터셋에서도 효과적으로 적용됨을 확인할 수 있었다.
또한, 모델의 하이퍼파라미터에 대한 민감도 분석과 시간 소비에 대한 실험을 통해 모델의 견고성과 효율성을 입증했다.
이를 통해 GrDNFCS 모델이 실제 데이터에 대한 클러스터링 작업에 적합하며, 다양한 응용 가능성을 가지고 있음을 강조한다.
또한, GrDNFCS 모델의 우수성을 확인하기 위해 다양한 평가 지표를 활용하여 그 성능을 명확히 제시하고, 해당 모델의 실제 응용 가능성과 잠재적 가치를 강조한다.
마지막으로, GrDNFCS 모델의 성과를 강조하고, 미래 연구 방향에 대한 제언을 통해 해당 연구의 중요성과 확장 가능성에 대해서 말한다..