Soft Contrastive Learning for Visual Localization

Abstract

Image Retrieval(이미지 검색)을 통한 Localization은 간단한 매핑 및 매칭 기술 덕분에 큰 비용을 들이지 않고 확장이 가능하다. 그러나 이 방법론의 localization accuracy는 contrastive learning(대조학습)을 통해 얻은 기본 이미지 특성의 품질에 영향을 받는다.
그리고 대부분의 대조학습 방법론은 서로 다른 클래스를 구별하기 위한 특성을 위주로 학습하지만, Localization의 경우에는 명확한 클래스를 정의하기가 어렵기 때문에 anchor image(학습 대상)에 대한 기하학적 근접성을 측정하여 인위적으로 positive/negative class로 구분짓는다.

하지만 이 논문에서는 기존의 기하학적 근접성을 토대로 인위적인 클래스 구분을 짓는 것은 localization 특성을 학습하는 데에 문제를 일으킬 수 있다고 한다. 또한, 기하학적 근접성을 측정해서 positive와 negative 클래스로 나눈다는 것은 threshold가 있다는 뜻이고, threshold에 인접한 이미지들의 경우엔 구분짓기가 굉장히 모호해진다는 단점이 존재한다.
이러한 문제들을 피하기 위해서, 논문은 soft positive/negative 클래스를 부여하여 기하학적 공간과 특성 공간에서 점진적으로 가까운 이미지와 먼 이미지를 구분한다. 그 결과, 4개의 대용량 벤치마크 데이터셋에서 SOTA를 달성했고, 기존의 retrieval 기반 방법론보다 우수함을 보였다.

Introduction

이미지 검색 기반 위치 추정은 단순하고 확장 가능한 방법으로, 고품질의 넓은 시야 이미지를 사용하여 특정 위치를 고유하게 나타낼 수 있다. 시각 기반 위치 추정은 로봇 공학과 증강 현실 등 여러 응용 분야에서 효과적이지만, 대규모 환경에서는 높은 계산 요구 때문에 제한된다. GPS와 같은 추가 센서를 사용할 수 없는 경우, 이미지 검색 기반 위치 추정이 좋은 대안이 된다.

기존의 시각 기반 위치 추정 방법은 주로 구조 기반 접근법(SfM, SLAM)과 검색 기반 접근법으로 나눌 수 있다. 검색 기반 위치 추정은 간단한 매핑 및 매칭 덕분에 저렴하며, 최근 이미지 특징 학습의 발전으로 더욱 유용해졌다. 대부분의 위치 추정 특징 학습 방법은 분류를 위한 학습에 기반하고 있으며, 대비 학습을 사용하여 서로 다른 카테고리를 구별하는 특징을 학습한다.

그러나 위치 추정에서는 자연스러운 클래스 정의가 없어, 인위적으로 긍정/부정 클래스로 나누는 것이 문제가 된다. 이러한 인위적인 분할은 근접성 임계값 근처의 이미지에 대한 모호한 supervision 때문에 바람직하지 않다. 이를 해결하기 위해, 소프트 긍정/부정 할당 방식을 제안한다. 이 방식은 기하학적 및 특징 공간에서 점진적인 구분을 통해 보다 효과적인 학습을 가능하게 한다.

이 논문의 주요 기여점은 3가지로 요약할 수 있다.

1. 위치 추정 특징 학습을 위한 공식 이론적 프레임워크 제안.
2. 제안된 프레임워크 내에서 새로운 손실 함수 공식화.
3. 네 가지 대규모 데이터셋에서 제안된 방법의 우수성 입증.

Related Work

Visual localization features

기존 연구들은 크게 3가지로 구분지을 수 있다.

1. 장소 인식에 대해서 학습 및 추론
2. 장소 인식에 대해서 학습한 후, 지역화(localization)에 대해서 추론
3. localization에 대해서 학습 및 추론

1번 방법론은 place를 recognize하기 위해 필요한 특성들을 학습하고, 같은 세팅에서 테스트를 진행한다.
2번 방법론이 이 논문에서 앞서 논의한 내용인데, targe place를 recognize하기 위한 방법론임에도 불구하고 visual localization task에 일반화된다.
3번 방법론은 visual localization에 따르는 방법론이다. 이 논문의 방법론 또한 3번 카테고리에 해당된다. 하지만 기존의 방법론들은 hard assignments인 반면, 이 논문은 이를 soft assignments로 바꿨기 때문에 방법론적으로 차이가 분명하다.

Assignments for contrastive learning

기존 기술들을 3가지 카테고리로 분류하면 다음과 같다.

1. hard assignments
2. hybrid assignments
3. soft assignments

hard assignment는 이미지를 엄격하게 이진 분류한다.(anchor image에 기반하여 positive와 negative로 분류) hybrid assignment 또한 이진 categorization을 진행하지만, 각 카테고리 내의 샘플에 대해서 서로 다른 처리를 진행한다. 예를 들면, feature를 찾을 때, feature distance가 positive pairs의 기하학적 거리에 비례하도록 찾는 방법론이 있다.
다음으로, soft assignment는 샘플들을 이진 분류하지 않는다. 이 논문에서 제안하는 방법론 또한 soft assignment 기반이지만 기하학적 거리가 멀어도 featuer distance가 적절하다면 해당 샘플은 충분하다고 판단하는 점(굳이 기하학적 거리와 비례하지 않아도 괜찮다는 것)에서 기존 논문들과 본질적으로 다르다.
모든 pair에 대해서 비례성을 적용하면 geometric map을 저장하는데 있어서 문제가 발생한다. (이 때문에 위에서 예시로 언급한 기존 연구에서도 positive pair에 대해서만 진행한 것)

이 논문에서는 기하학적 공간에서 feature간 거리가 가깝고, feature space에서 거리가 먼 경우에 anchor 쪽으로 당겨진다 (반대의 경우에도 마찬가지).

Problem Formulation and Background

3.1 Preliminaries

데이터(D) 구성은 (I,x) 쌍으로 구성되며, I는 이미지 샘플, x는 이미지의 기하학적 위치 정보이다. 그리고 $\phi$는 CNN 모델이고, 세타는 모델 파라미터이다. 이를 통해서 이미지를 하나의 feature space에 매핑시킬 수 있다.
retrieval-based localization을 위해서는 image pair 간에 기하학적 근접성을 측정해서 ordering한 것이 feature간에 유클리디언 거리를 ordering한 것을 따르게하는 파라미터 세타($\theta$)를 학습해야 한다.
대용량 데이터셋에서는 학습 동안에 이를 다 계산한다는게 컴퓨팅 자원적으로 쉽지 않다. 따라서 이 논문은 anchor-based learning (A={a}로 표현되는 anchor features를 랜덤하게 선택)을 기본 셋업으로 가져간다.

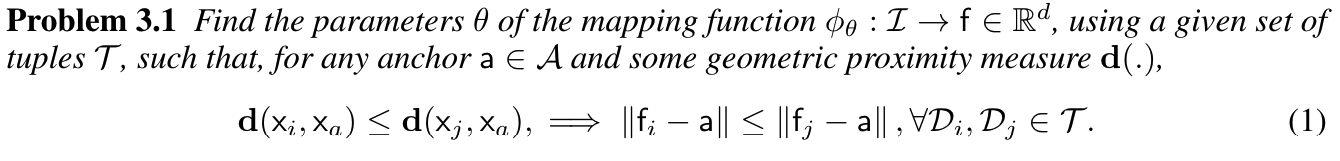
feature space에서의 유클리디언 거리는 retrieval process를 진행할 때, computation cost를 낮추기 위해서 사용한 것이다. 즉, 기하학적으로 가까운 이미지를 찾을 때, feature distance만을 이용해서 충분히 찾을 수 있다는 뜻이다. 이 논문에서 제시하는 솔루션을 설명하기 전에, 지금까지 사용된 매핑 함수 $\theta$를 학습하는 표준 접근법들을 살펴봐야 한다.

3.2 Learning by hard assignments revisited

hard assignment는 모든 anchor에 대해서 positive(P)와 negative(N)으로 이진 분류된다. 기하학적 공간에서 근접한지에 대한 임계치는 임의로 $\tau_1, \tau_2$로 지정하고, $\tau_1 <= \tau_2$를 만족하며, $P = \{f_i|d(x_i,x_a)<\tau_1 \} = \{p\}$, $N = \{f_i|d(x_i,x_a)>=\tau_2 \}=\{n\}$를 따른다.

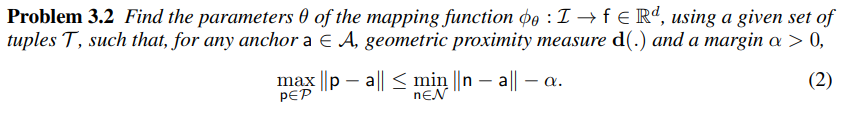
retrieval-based localization에서 3.2와 같은 수식은 몇 가지 의문점을 남긴다.

1. 이미지에 대한 처리 없이 임의로 설정한 $\tau_1, \tau_2$
2. problem 3.1에서 원하는 형태가 아님
3. 임계치 $\tau_1, \tau_2$가 동일해졌을 때, supervision이 모호해짐

3번에 대해서 좀 더 자세히 설명하자면,

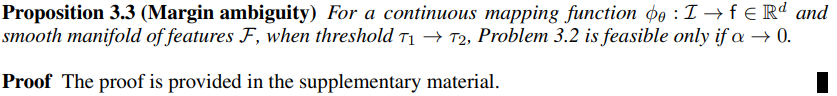
매핑 함수가 기하 공간 전반에 걸쳐 이미지를 연속적으로 매핑할 수 있다면, threshold $\tau_1$ -> $\tau_2$가 되었을 때, Problem 3.2 식이 만족하기 위해서는 $\alpha=0$이 되어야 한다.

전반적으로 요약하자면, 만약 기하적 측정에 따라 feature distance가 ordering될 수 있고, 기하 공간 전체에서 연속적으로 이미지를 사용할 수 있다면, $\tau_1 == \tau_2$가 될 때, $\alpha$가 무조건 0이 되어야 수식 (2)에 대한 올바른 해를 가질 수 있다. 게다가, 이렇게 구한 해도 순서를 유지해주지는 못한다.

다시 말해, 주어진 매핑 함수가 이미지의 기하학적 거리와 특징 거리를 일관되게 유지할 수 있을 때, 두 임계값 $( \tau_1 )$과 $( \tau_2 )$가 같아지는 경우 마진 $( \alpha )$가 0이 되어야 문제 2의 실행 가능한 해가 존재한다는 것을 의미한다. 또한, 이러한 해는 특징 거리와 기하학적 거리의 원하는 순서를 유지하지 못한다. (max positive와 min negative가 같아지는 경우가 생기기 때문인 것 같음.)

Learning by Soft Assignments

이 논문에서 제시하는 방법론은 이미지를 엄격하게 positive와 negative로 이진 분류 하는 것이 아니라, feature distance와 geometric proximity measure를 사용하여 positiveness와 negativeness에 대한 score를 매기고 $s^+, s^-$로 명명한다.

contrastive learning 특성 상, 거리가 멀어지면 negativeness가 증가해야 하고, 거리가 가까워지면 positiveness가 증가해야 한다. 따라서 y가 샘플 간 거리라고 가정했을 때, 영향 함수 $g^+, g^-$가 contrastive learning 특성을 따라야 한다.
Definition 4.1의 제약 조건들을 보면 이를 만족함을 알 수 있다.(거리는 0 이상, 거리가 0일 때 positive 영향 함수가 negative 영향 함수보다 큼, y가 커지면 negative 영향 함수가 positive 영향 함수보다 그 값이 커짐 등)