An Inductive Bias for Tabular Deep Learning

Abstract

딥러닝 방법은 이미지, 텍스트, 오디오와 같은 데이터 모델링 작업에서 최첨단 성능을 보여주지만, tabular 데이터에서는 tree based approach보다 성능이 떨어지는 경향이 있다. 이 논문에서는 tabular 데이터의 heterogeneous한 특성으로 인해 타겟 함수가 불규칙해지고, 신경망이 smooth한 함수를 학습하는 경향이 성능 차이의 주요 원인이라고 가정했다.
스펙트럼 분석 도구를 이용해 높은 불규칙성을 가지는 tabular 데이터셋에 대하여 scaling / ranking transformation 등으로 부드럽게 할 수 있지만, 이러한 변환은 정보 손실이나 최적화 문제를 초래할 수 있다. 이를 해결하기 위해 주파수 감소(frequency reduction)를 유도하는 새로운 neural network layer를 제안했다. 이 layer는 input feature의 저주파 표현(low-frequency representation)을 학습하도록 하여 성능을 향상시키고, 수렴 속도를 높인다. 제안된 방법은 14개의 tabular 데이터셋에서 신경망의 성능을 크게 향상시키고, 수렴 속도를 가속화한다.

Introduction

tabular data의 도전 과제

tabular data는 가장 간단하고 자연스러운 데이터 설명 방법 중 하나이지만, 이질적인 열을 포함하고 있어 딥러닝 모델에게 큰 도전 과제를 제시한다. 최근 연구에서는 여러 딥러닝 접근법을 트리 기반 모델과 비교한 결과, 트리 기반 모델이 tabular 데이터에서 최고의 성능을 보이는 것으로 나타났다. 그럼에도 불구하고, 딥러닝 모델은 미분 가능한 손실 함수를 사용하고, 의미 있는 고차원 데이터 표현을 학습할 수 있으며, 대규모 데이터셋으로 확장할 수 있다는 여러 장점을 제공한다. 이미지 생성 및 언어 모델링에서 신경망의 빠른 발전은 복잡한 정보를 인코딩할 수 있는 능력을 명확히 보여준다. tabular 데이터셋을 포함한 작업에서 이러한 이점을 최대한 활용하려면 딥러닝 모델이 이러한 형태의 데이터에서 성능이 부족한 이유를 파악하고 해결하는 것이 중요하다.

스펙트럼 편향

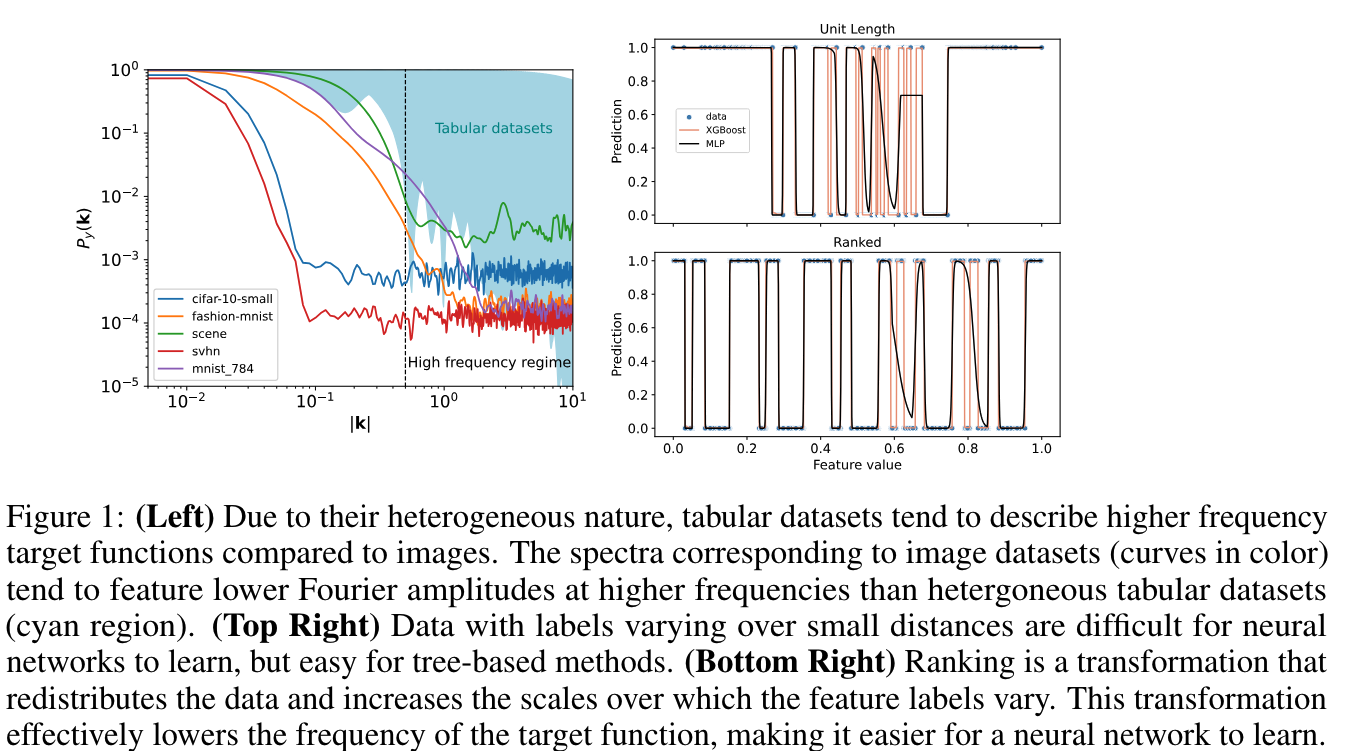
합성 및 이미지 데이터에 대한 몇 가지 중요한 연구는 신경망이 저주파 성분을 더 쉽게 학습하는 경향이 있다는 것을 지적한다. 이러한 스펙트럼 편향은 tabular 데이터에서도 유사하게 나타나며, 딥러닝 모델이 표형 데이터에서 고주파 성분을 학습하는 데 어려움을 겪는 원인 중 하나로 작용한다.

주파수 저감의 유도 편향

논문에서는 주파수 저감을 유도 편향으로 사용하는 방법을 제안하였다. 이는 신경망 훈련 중 입력 특성의 저주파 표현을 학습하도록 장려하는 훈련 가능한 층을 도입하여 구현된다. 이러한 층은 목표 함수의 주파수 스펙트럼을 조정하여 결과 신경망의 성능을 향상시킨다.

실험 설정 및 결과

논문은 14개의 벤치마크 분류 데이터셋을 사용하여 제안된 방법을 평가하였다. 실험 결과, 제안된 방법이 모든 데이터셋에서 신경망의 성능을 향상시키고 수렴 속도를 높이는 데 성공하였다. 특히, 높은 주파수 성분을 가진 데이터셋에서 성능 향상이 두드러졌다. 주파수 저감 층을 도입한 신경망은 기존의 딥러닝 모델과 비교하여 성능이 크게 향상되었으며, 트리 기반 모델과 비교했을 때도 경쟁력 있는 성능을 보였다.

이 논문은 tabular 데이터에 대한 딥러닝 모델의 성능을 향상시키기 위해 주파수 저감을 유도 편향으로 사용하는 새로운 접근 방식을 제안하였다. 제안된 방법은 입력 특성의 저주파 표현을 학습하도록 장려하여 목표 함수가 더 규칙적인 공간에서 신경망이 작동할 수 있도록 한다. 이를 통해 딥러닝 모델의 성능을 크게 향상시킬 수 있음을 실험적으로 입증하였다. 향후 연구에서는 다양한 데이터셋과 딥러닝 모델 구조에 대한 적용 가능성을 탐색하여 제안된 방법의 일반성을 평가할 필요가 있다.

Related Works

신경망의 스펙트럼 분석

신경망의 스펙트럼 특성에 대한 연구는 딥러닝의 학습 행동을 이해하는 데 중요한 역할을 한다. Fourier 분석을 사용하여 신경망이 목표 함수의 저주파 성분을 먼저 학습하는 경향이 있다는 것이 밝혀졌다. 이를 스펙트럼 편향 또는 주파수 원리라고 하며, 이는 신경망이 저주파 정보를 더 잘 학습하는 특성을 나타낸다. 비균일 밀도의 데이터를 연구한 결과, 데이터 밀도와 주파수가 경사 하강법의 행동에 영향을 미친다는 것이 관찰되었다.

tabular deep learning

tabular 데이터에서 딥러닝 모델이 트리 기반 모델보다 성능이 떨어지는 이유로, 다양한 방법들이 제안되었다. 예를 들어, 순차적 주의를 사용하여 각 추론 단계에서 사용할 특성을 선택하는 방법, 손상된 변형에서 입력 샘플을 복구하는 사전 작업을 도입한 방법, 행 및 열 주의를 결합한 방법 등이 있다. 이러한 접근법들은 모두 tabular 데이터에서 딥러닝 모델의 성능을 향상시키기 위한 노력의 일환이다. 특히, 수치 및 범주형 특성을 효과적으로 임베딩하는 방법, 단순 MLP를 위한 최적의 하이퍼파라미터 조합을 찾는 방법 등이 제안되었다.

이러한 연구들은 딥러닝 모델이 tabular 데이터에서 성능을 발휘하기 위해 필요한 다양한 접근법을 제시하고 있다. 특히, 스펙트럼 편향을 줄이기 위한 노력은 신경망이 고주파 정보를 더 잘 학습할 수 있도록 하는 데 중요한 역할을 한다. 이는 딥러닝 모델이 더 복잡한 데이터에서 우수한 성능을 발휘하는 데 기여할 수 있다.

기존 연구들은 신경망의 스펙트럼 특성을 이해하고, 이를 통해 tabular 데이터에서 딥러닝 모델의 성능을 향상시키기 위한 다양한 방법을 제안하였다. 이러한 연구들은 스펙트럼 편향을 줄이기 위한 방법, 수치 및 범주형 특성을 효과적으로 임베딩하는 방법 등을 포함하며, 이는 딥러닝 모델이 더 다양한 데이터 유형에서 우수한 성능을 발휘할 수 있도록 하는 데 기여할 것이다.

Methodology

Methodology 요약 및 수식 설명

배경

표형 데이터셋 $(D = \{(x_i, y_i)\}_{i=1}^{N})$에 대해 $(x_i \in \mathbb{R}^n)$이고, $(y_i \in \{0, 1\}^m)$인 분류 작업을 고려한다. 이 작업은 분류기를 학습하는 것이다 $(f : \mathbb{R}^n \rightarrow \{0, 1\}^m)$. 단순화를 위해 $(m = 1)$로 설정하고, $(y = 1)$을 소수 클래스(minority class)로 설정한다.

데이터에 의해 암묵적으로 정의된 목표 함수(target functions)를 포함하여 다양한 함수의 주파수 스펙트럼에 관심이 있다. 각 데이터셋에서 제공된 데이터 포인트에서만 레이블이 정의되어 있으므로, 특정 스케일에서 변동의 강도를 측정하는 스펙트럼 분석 방법에 의존한다. 이러한 방법 중 하나는 비균일 이산 푸리에 변환(NUDFT)이다.

비균일 이산 푸리에 변환(NUDFT)

함수 $(f(x))$와 점 집합 $(X = \{x_i\}_{i=1}^{N})$에 대해, NUDFT는 주파수 벡터 $(k \in \mathbb{R}^n)$의 함수로 정의된다:

이 식은 $(f(x))$의 다차원 연속 푸리에 변환(FT)을 데이터 포인트 $(X)$로 대표되는 경험적 분포로 가중한 근사치로 해석될 수 있다. 주어진 $(k)$에서 식 (1)에 의해 근사된 푸리에 변환은 복소수 지수로의 투영에서 $(e^{2\pi i k \cdot x})$ 항의 계수에 해당한다. 따라서 한 함수가 다른 함수보다 고주파수임을 나타내는 자연스러운 정의는, 전자가 지정된 저주파수 영역을 벗어난 더 큰 크기의 푸리에 진폭을 가지는 것이다. 이를 구체적으로 비교하기 위해, $(k = k k̂)$로 정의하고, $(k̂)$는 $(\mathbb{R}^n)$의 단위 벡터이다. 주어진 $(k)$ 방향을 따라 함수의 제곱된 NUDFT 진폭 $(P_f(k) = |\tilde{f}_X(k)|^2)$의 크기를 비교할 수 있다:

목표 함수 스펙트럼의 스펙트럼 분석

목표 함수가 정의된 데이터 포인트 외부의 특성을 이해하기 위해 연속 푸리에 변환을 사용하여 목표 함수의 주파수 스펙트럼을 분석한다. 함수 $(g(x))$의 푸리에 변환을 $(F_x[g(x)](k))$로 나타낸다. 합성 정리에 따르면:

여기서 $(\text{sinc}(x) = \frac{\sin(\pi x)}{\pi x})$이다. 다른 $(\Delta_i)$ 선택은 데이터 포인트 간의 최소 근접 거리를 기준으로 한 공통 $(\Delta_i = \Delta = \min \{|x_i - x_j)|_\infty\})$ 선택으로 단순화할 수 있다. 이 경우, $(|k|_\infty \ll 1/(\pi \Delta))$ 한계에서:

여기서 오른쪽 항은 $(k = 0)$에서의 값을 정규화하는 절차를 사용할 때 상수 차원 스케일링 인자를 제외한 NUDFT와 일치한다. 따라서, NUDFT는 주파수가 데이터셋의 최소 근접 거리의 역수로 설정된 단순 목표 함수의 스펙트럼 특성을 재현한다.

주파수 저감 유도 편향의 구현

제안된 주파수 저감 유도 편향은 입력 특성의 저주파 표현을 학습하도록 장려하는 신경망 층으로 실현된다. 이 층은 목표 함수가 더 규칙적인 공간에서 네트워크가 작동할 수 있도록 한다. 제안된 방법은 완전 연결 층보다 적은 계산 복잡성을 도입하면서도 신경망 성능을 크게 향상시키고, 표형 데이터셋에서 수렴 속도를 높인다.

제안된 주파수 저감 유도 편향은 표형 데이터에 대한 딥러닝 모델의 성능을 향상시키는 데 중요한 역할을 할 수 있음을 보여주었다. 향후 연구에서는 다양한 데이터셋과 딥러닝 모델 구조에 대한 적용 가능성을 탐색하여 제안된 방법의 일반성을 평가할 필요가 있다.

Experiments and Results

평가 지표 및 실험 설정

이 논문에서는 세 가지 주요 메트릭을 중심으로 평가를 진행하였다: 성능(performance), 수렴 속도(rate of convergence), 학습된 함수의 불규칙성(irregularity)이다. 각 메트릭은 다음과 같이 정의되었다:

1. 성능: 정확도(accuracy)와 수신자 조작 특성 곡선 아래 영역(AUROC)을 사용하여 평가되었다.
2. 수렴 속도: 검증 손실(validation loss)을 최소화하는 데 필요한 평균 학습 에포크(epoch) 수로 평가되었다.
3. 학습된 함수의 불규칙성: 주성분 분석(principal component analysis, PCA)을 사용하여 주요 주성분(principal components, PCs)을 따라 총 고주파수 성분의 크기로 측정되었다.

데이터셋

14개의 벤치마크 분류 데이터셋을 사용하여 제안된 방법을 평가하였다. 이 데이터셋들은 다양한 크기와 특성을 가지고 있으며, 트리 기반 모델과 신경망 간의 성능 차이를 보여주는 데 사용되었다. 데이터셋은 Table 2에서 확인할 수 있다.

실험 방법

주파수 감소와 신경망

논문에서는 주파수 감소가 신경망의 성능에 미치는 영향을 분석하기 위해 다양한 변환 방법을 적용하였다. 정규화 및 집계 통계를 사용하여 각 변환 방법의 일반적인 동작을 강조하였다. 제안된 방법은 기존의 모든 변환 방법을 능가하였으며, 특히 빠르게 수렴하는 것으로 나타났다. 모든 변환 방법은 단위 스케일링된 데이터에 비해 학습된 함수의 주파수를 감소시켰으나, 제안된 방법은 성능 증가와 변환의 부작용 간의 균형을 잘 맞추어 효과적인 유도 편향을 제공하였다.

성능 비교

제안된 방법은 단순 신경망 모델(MLP)의 성능을 크게 향상시켰으며, 트리 기반 모델인 XGBoost와 비교했을 때도 경쟁력 있는 성능을 보였다. 특히, 높은 주파수 성분을 가진 데이터셋에서 제안된 방법의 성능 향상이 두드러졌다. 이는 주파수 저감이 신경망이 고주파 성분을 학습하는 데 도움을 준다는 것을 보여준다.

목표 함수 주파수의 영향을 받는 성능

다양한 목표 함수 주파수를 가진 합성 데이터셋을 사용하여 추가 실험을 수행하였다. 그 결과, 낮은 목표 함수 주파수에서는 모든 방법이 유사한 성능을 보였으나, 목표 함수 주파수가 증가함에 따라 신경망의 성능이 감소하는 현상을 관찰할 수 있었다. 제안된 방법은 다른 방법들보다 높은 주파수 목표 함수에 대해 일관되게 우수한 성능을 보였으며, 가장 높은 주파수 목표 함수에 대해 가장 강력한 성능을 보였다.

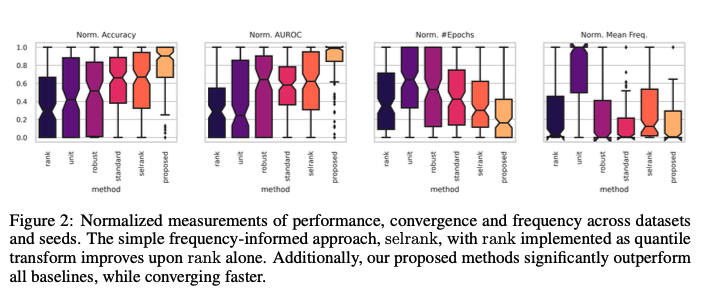
Figure 2는 다양한 변환 방법에 따른 주파수 감소와 신경망 성능의 변화를 보여준다. 제안된 방법이 다른 변환 방법에 비해 더 나은 성능을 보이며, 빠르게 수렴하는 것을 확인할 수 있다.

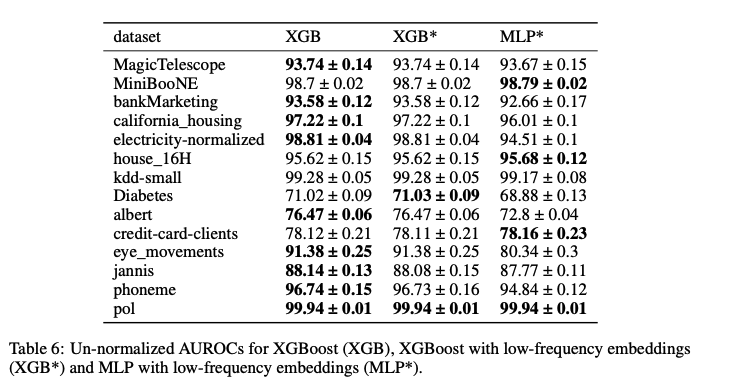
Table 6은 제안된 방법과 기존 방법(MLP, XGBoost 등)의 성능 비교를 보여준다. 제안된 방법이 모든 데이터셋에서 높은 성능을 보이며, 특히 높은 주파수 성분을 가진 데이터셋에서 두드러진 성능 향상을 나타낸다.

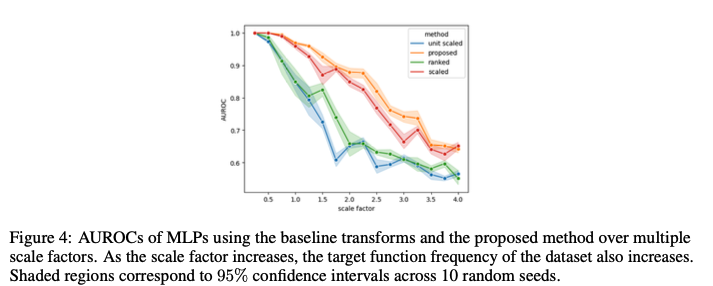
Figure 4는 다양한 목표 함수 주파수를 가진 합성 데이터셋에서 제안된 방법의 성능 변화를 보여준다. 높은 주파수 목표 함수에 대해 제안된 방법이 일관되게 우수한 성능을 보이는 것을 확인할 수 있다.

주파수 감소는 신경망이 학습하는 함수의 주파수 스펙트럼을 변화시켜 신경망이 고주파 성분을 더 잘 학습할 수 있도록 도와준다. 이는 특히 표형 데이터에서 중요한데, 표형 데이터는 종종 고주파 성분을 많이 포함하고 있기 때문이다. 제안된 방법은 이러한 고주파 성분을 효과적으로 줄여 신경망의 성능을 크게 향상시켰다.

실험 결과, 제안된 방법이 신경망의 성능을 향상시키는 데 효과적임을 입증하였다. 특히, 제안된 방법은 빠른 수렴 속도와 높은 성능을 동시에 달성하였으며, 이는 실제 적용에 있어 중요한 장점이다. 또한, 다양한 데이터셋에서 일관되게 높은 성능을 보임으로써 제안된 방법의 일반성을 확인할 수 있었다.

이 논문은 신경망의 스펙트럼 편향이 표형 데이터셋에서 신경망 성능에 미치는 영향을 연구하였다. 제안된 주파수 저감 유도 편향은 신경망이 목표 함수의 고주파 성분을 줄여 더 나은 성능을 발휘할 수 있도록 하였다. 실험 결과, 제안된 방법은 신경망의 성능을 크게 향상시키고, 학습 에포크 수를 줄이는 데 효과적임을 보여주었다. 향후 연구에서는 다른 신경망 구조와 데이터셋에 대한 적용 가능성을 탐색하여 제안된 방법의 일반성을 평가할 필요가 있다.

Conclusion

이 논문에서는 신경망의 스펙트럼 편향이 표형 데이터셋에서 신경망 성능에 미치는 영향을 연구하였다. 표형 데이터셋은 목표 함수의 불규칙성이 높아 신경망의 성능에 부정적인 영향을 미친다는 것을 보여주었다. 이러한 문제를 해결하기 위해 주파수 저감을 유도 편향으로 도입하는 방법을 제안하였다. 제안된 방법은 학습된 함수의 불규칙성을 줄여 신경망의 성능을 크게 향상시키고, 수렴 속도를 높이는 데 기여하였다. 우리는 주파수 저감 유도 편향을 표형 딥러닝을 위한 새로운 방향으로 제안하지만, 해당 편향을 실현하는 데 있어서는 아직 초기 단계에 있다. 예를 들어, 스펙트럼 분석의 관점에서 다른 표형 딥러닝 접근법의 성능 향상을 설명할 수 있는지 여부를 조사할 필요가 있다.