SVM

🎉 Introduction

SVM: 매우 강력하고 비선형 분류, 회귀, 이상치 탐색에도 사용할 수 있는 다목적 머신러닝 모델

5.1 선형 SVM 분류

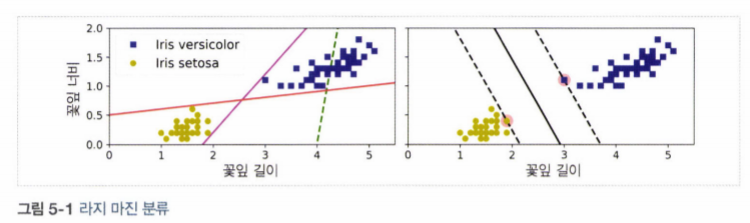
• SVM Classification는 클래스 사이에서 가장 폭이 넓은 도로를 찾는 것으로 생각 할 수 있음.
• 라지 마진 분류(large margin classification) 이라고도 불림.

• 도로의 폭은 도로 경계에 위치한 샘플에 의해 전적으로 결정되며, 이 샘플을 서포트 벡터(Support Vector)라고 함

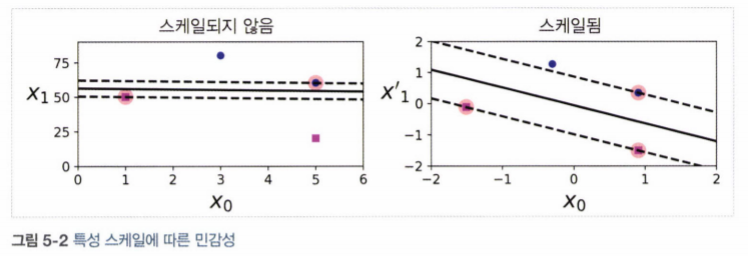
• SVM은 특성의 스케일에 민감하기에, 특성의 스케일을 조정하면(StandardScaler를 사용하면) 결정 경계가 훨씬 좋아짐.

5.1.1 소프트 마진 분류

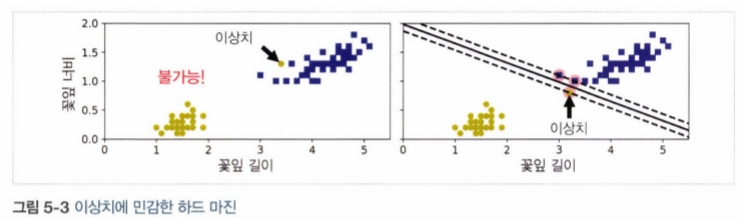
하드 마진 분류(Hard Margin Classification): 모든 샘플이 도로 바깥쪽으로 올바르게 분류되어 있는 것

• 데이터가 선형적으로 구분되어 있어야 함
• 이상치에 민감함
  

🧨 위 그림과 같은 문제를 피하려면 유연한 모델이 필요!

👉 즉, 라지 마진 (도로의 폭을 가능한 한 넓게 유지하는 것) 과 마진 오류(margin violation : 샘플이 도로 중간이나 심지어 반대쪽에 있는 경우) 사이에 적절한 균형을 잡아야 함.

💥 소프트 마진 분류(Soft Margin Classification)

• 사이킷런의 SVM모델에서는 C하이퍼파라미터를 사용해 이 균형을 조절할 수 있음
• C값을 줄이면 도로의 폭이 넓어지지만, 마진 오류도 커집니다.

5.2 비선형 SVM분류

일반적으로 선형적으로 분류할 수 없는 데이터 셋이 더 많음.

• 비선형 데이터 셋을 다루는 한가지 방법은 다항 특성과 같은 특성을 더 추가하는 것

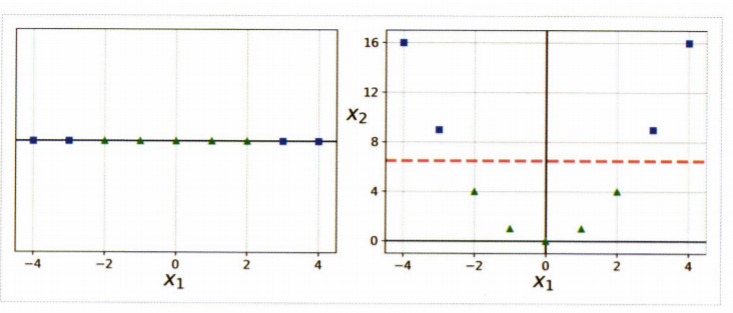
왼쪽 그림은 선형적으로 구분이 안되지만 $x_2 = {(x_1)}^2$을 추가하여 만들어진 2차원 데이터셋은 선형적으로 구분이 가능해짐.

5.2.1 다항식 커널

다항식 특성을 추가하는 것은 간단하지만, 한계가 있음.

• 낮은 차수의 다항식은 매우 복잡한 데이터셋을 잘 표현하지 못함
• 높은 차수의 다항식은 굉장히 많은 특성을 추가하므로 모델을 느리게 함

5.2.2 유사도 특성 추가

비선형 특성을 다루는 또 다른 기법은, 각 샘플이 특정 랜드마크(landmark) 와 얼마나 닮았는지 측정하는 유사도 함수(similarity function) 로 계산한 특성을 추가하는 것

Gaussian RBF
$ϕγ(x,ℓ)=exp(−γ∥x−ℓ∥2)$

• 이 함수의 값은 0부터 1까지 변화하며 종모양을 가짐
• gamma는 0보다 커야 되며, 값이 작을수록 폭이 넓은 종 모양이 나타남

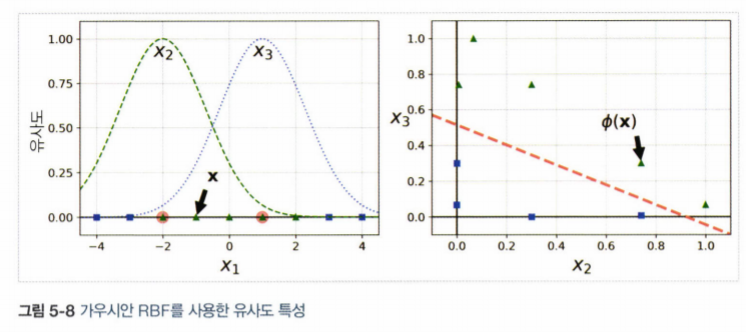
5.2.3 가우시안 RBF 커널

유사도 특성도 머신러닝 알고리즘에 유용하게 사용될 수 있음.

• 그러나 추가 특성을 모두 계산하려면 연상 비용이 많이드는데, 특히 훈련 세트가 클 경우 더욱 그러함
• 가우시안 RBF 커널을 추가 하는 것으로 같은 효과를 얻을 수 있음
  

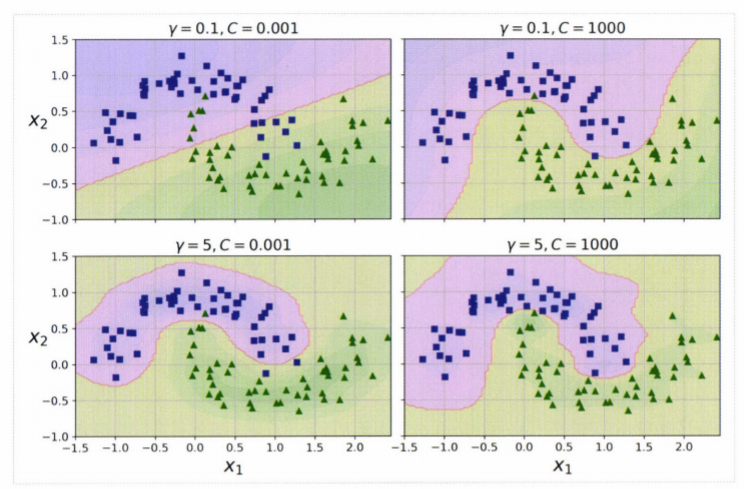
🔔 가우시안 RBF 커널

• gamma가 높아지면?
  종 모양 그래프가 좁아져서 각 샘플의 영향 범위가 줄어, 경계가 데이터들을 따라 구불구불해짐
• gamma가 낮아지면?
  샘플이 넓은 범위에 걸쳐 영향을 주므로 결정경계가 부드러워짐

✔ 따라서, 모델이 과대적합일 경우엔 감소시켜야 되고 과소적합일 경우에는 증가시켜야 함