문제
일차원 좌표상의 점 N개와 선분 M개가 주어진다. 이때, 각각의 선분 위에 입력으로 주어진 점이 몇 개 있는지 구하는 프로그램을 작성하시오.
입력
첫째 줄에 점의 개수 N과 선분의 개수 M이 주어진다. (1 ≤ N, M ≤ 100,000) 둘째 줄에는 점의 좌표가 주어진다. 두 점이 같은 좌표를 가지는 경우는 없다. 셋째 줄부터 M개의 줄에는 선분의 시작점과 끝점이 주어진다. 입력으로 주어지는 모든 좌표는 1,000,000,000보다 작거나 같은 자연수이다.
출력
입력으로 주어진 각각의 선분 마다, 선분 위에 입력으로 주어진 점이 몇 개 있는지 출력한다.
예제 입력 1
5 5
1 3 10 20 30
1 10
20 60
3 30
2 15
4 8예제 출력 1
3
2
4
2
0문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.Arrays;
import java.util.StringTokenizer;
public class BJ11663 {
static int[] point;
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
int N=Integer.parseInt(st.nextToken());
int M=Integer.parseInt(st.nextToken());
point=new int[N];
st=new StringTokenizer(br.readLine());
for(int i=0;i<N;i++){
point[i]=Integer.parseInt(st.nextToken());
}
Arrays.sort(point);
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
// 이분탐색 -> 가능한 위치 인덱스 가져오기
int start_idx=binarySearch(start,0);
int end_idx=binarySearch(end,1);
System.out.println(end_idx-start_idx);
}
}
private static int binarySearch(int start, int check) {
int left=0;
int right= point.length-1;
if(check==0){
while(left<=right){
int mid=(left+right)/2;
if (point[mid] < start) {
left = mid+1;
} else {
right = mid-1;
}
}
return left;
}
else{
while(left<=right){
int mid=(left+right)/2;
if(point[mid]>start){
right=mid-1;
}
else{
left=mid+1;
}
}
return right+1;
}
}
}입력으로 주어지는 좌표의 범위가 1,000,000,000 까지 들어가기 때문에 이분탐색을 이용해야하는 문제였다.
이분탐색은 기준점을 정해두고 기준점보다 작은 경우에는 왼쪽으로, 큰 경우에는 오른쪽으로 이동하여 탐색을 반복하여 값을 찾아내는 방식이다.
- 탐색할 배열은 정렬되어야한다.
- 보통 기준점은 mid 값으로 정한다.
고려할 점
이번 문제에서는 어떤 값을 기준으로 잡을지, 탐색이 끝나면 어떤 값을 return 할지 고려해야한다.
우선, 이 문제에서는 인덱스를 기준으로 탐색을 수행한다.
예를 들어, 1 ~ 10 의 범위에 들어가는 숫자가 몇 개 있는지 파악하려면 1 3 10 20 30의 숫자들을 우선 오름차순으로 정렬한 뒤, 1보다 작거나 같은 인덱스의 위치와 10보다 크거나 같은 인덱스의 위치를 찾고
해당 인덱스들의 차를 구하면 해당 범위에 들어가는 숫자의 개수를 찾을 수 있다.
즉, 다음처럼 이해하면 된다.
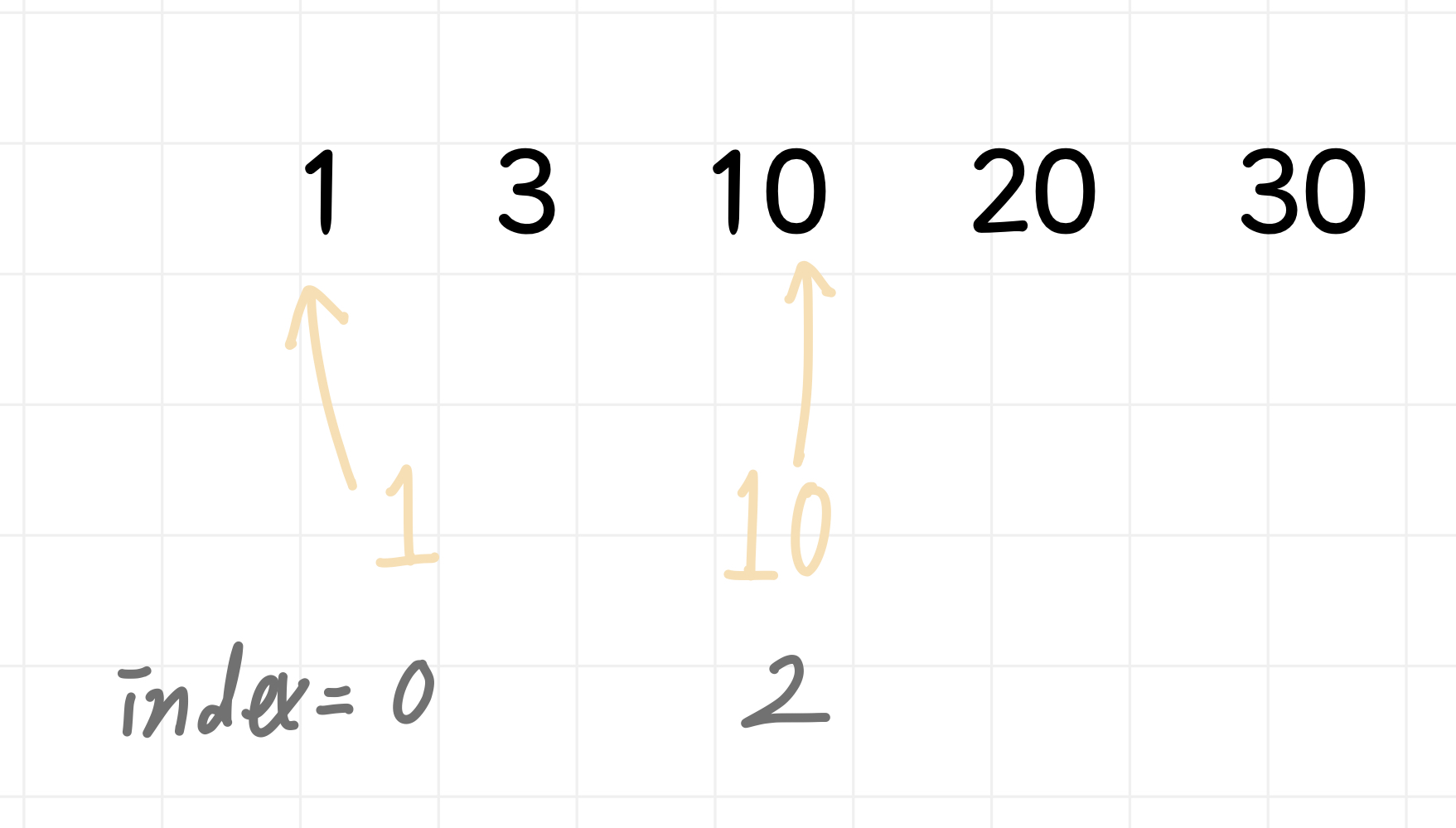
하지만 위 그림처럼 2-0을 하면 값이 2가 되어버리기 때문에 정답을 맞출 수 없다. 때문에 오른쪽 값은 탐색한 위치 + 1을 해주어야 정답을 찾을 수 있다.
이분탐색 준비하기
Arrays.sort(point);
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int start=Integer.parseInt(st.nextToken());
int end=Integer.parseInt(st.nextToken());
// 이분탐색 -> 가능한 위치 인덱스 가져오기
int start_idx=binarySearch(start,0);
int end_idx=binarySearch(end,1);
System.out.println(end_idx-start_idx);
}이분탐색을 위한 전제조건은 정렬이기 때문에 숫자들을 모두 정렬시켜주고 왼쪽 값, 오른쪽 값은 check라는 변수에 각각 0과 1을 담아 구분해주어 따로 값을 반환해준다.
그리고 반환된 값에서 오른쪽 값 - 왼쪽 값을 해주면 답을 구할 수 있다.
이분탐색
private static int binarySearch(int start, int check) {
int left=0;
int right= point.length-1;
if(check==0){
while(left<=right){
int mid=(left+right)/2;
if (point[mid] < start) {
left = mid+1;
} else {
right = mid-1;
}
}
return left;
}
else{
while(left<=right){
int mid=(left+right)/2;
if(point[mid]>start){
right=mid-1;
}
else{
left=mid+1;
}
}
return right+1;
}
}이분탐색을 위하여 left와 right 변수를 0과 point.lenght-1 인덱스로 잡아준다.
그리고 왼쪽 값을 찾는건지, 오른쪽 값을 찾는건지 구분하여 이분탐색을 진행한다.
왼쪽 값은 탐색된 값보다 작거나 같도록 찾아야하기 때문에 if문을 함께 묶어주고,
오른쪽 값은 탐색된 값보다 크거나 같아야 하기 때문에 if문을 함께 묶어준다.
그리고 point의 mid 인덱스 값보다 start 값이 크다면 left를 mid+1 값으로, 반대라면 right를 mid-1 값으로 바꿔주어 탐색을 진행한다.
모든 탐색이 끝나면 왼쪽 값의 경우에는 left 인덱스를 반환해주면 되는데
오른쪽 값의 경우에는 위의 예시를 고려하여 right 값이 아닌 right+1 값을 반환해주면된다.
문제를 다 풀고 나니까 간단했던 문제였는데 혼자 풀려고 하니 if문을 어떻게 묶어야하는지, right 값을 반환해야하는지 left를 반환해야하는지 헷갈려서 시간이 꽤 걸렸던 문제였다.
마지막에는 계속 틀렸다고 나와서 오류를 찾아보니 정렬을 제대로 해주지 않아 생겼던 문제였다.
이분탐색을 할때는 꼭 정렬을 해주자...
