문제
보물섬 지도를 발견한 후크 선장은 보물을 찾아나섰다. 보물섬 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 각 칸은 육지(L)나 바다(W)로 표시되어 있다. 이 지도에서 이동은 상하좌우로 이웃한 육지로만 가능하며, 한 칸 이동하는데 한 시간이 걸린다. 보물은 서로 간에 최단 거리로 이동하는데 있어 가장 긴 시간이 걸리는 육지 두 곳에 나뉘어 묻혀있다. 육지를 나타내는 두 곳 사이를 최단 거리로 이동하려면 같은 곳을 두 번 이상 지나가거나, 멀리 돌아가서는 안 된다.
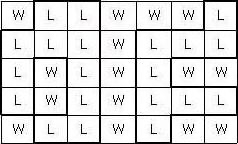
예를 들어 위와 같이 지도가 주어졌다면 보물은 아래 표시된 두 곳에 묻혀 있게 되고, 이 둘 사이의 최단 거리로 이동하는 시간은 8시간이 된다.
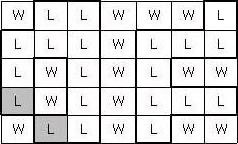
보물 지도가 주어질 때, 보물이 묻혀 있는 두 곳 간의 최단 거리로 이동하는 시간을 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 보물 지도의 세로의 크기와 가로의 크기가 빈칸을 사이에 두고 주어진다. 이어 L과 W로 표시된 보물 지도가 아래의 예와 같이 주어지며, 각 문자 사이에는 빈 칸이 없다. 보물 지도의 가로, 세로의 크기는 각각 50이하이다.
출력
첫째 줄에 보물이 묻혀 있는 두 곳 사이를 최단 거리로 이동하는 시간을 출력한다.
예제 입력 1
5 7
WLLWWWL
LLLWLLL
LWLWLWW
LWLWLLL
WLLWLWW예제 출력 1
8문제 풀이
package study.radish.month10;
import java.awt.*;
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
public class BJ2589 {
static char[][] map;
static boolean[][] visited;
static int[][] mapNum;
static int N,M;
static int dist,tmp;
static int[][] moves={{1,0},{0,1},{-1,0},{0,-1}};
public static class Node{
int x,y,depth;
public Node(int x, int y, int depth) {
this.x = x;
this.y = y;
this.depth = depth;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
N=Integer.parseInt(st.nextToken());
M=Integer.parseInt(st.nextToken());
map=new char[N][M];
mapNum=new int[N][M];
visited=new boolean[N][M];
dist=Integer.MIN_VALUE;
for(int i=0;i<N;i++){
map[i]=br.readLine().toCharArray();
}
// 육지별 번호 매기기
int cnt=1;
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
if(map[i][j]=='L' && !visited[i][j]){
bfs(i,j,cnt);
cnt++;
}
}
}
//각 육지별로 for문 돌려서 시작점마다 끝 노드까지의 거리 구하기
for(int c=1;c<=cnt;c++){
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
tmp=0;
if(mapNum[i][j]==c){
bfsNum(i,j,c);
if(tmp>dist){
dist=tmp;
}
}
}
}
}
System.out.println(dist);
}
private static void bfsNum(int i, int j, int cnt) {
boolean[][] tmpV=new boolean[N][M];
Queue<Node> queue=new ArrayDeque<>();
queue.offer(new Node(i,j,0));
tmpV[i][j]=true;
while(!queue.isEmpty()){
Node n=queue.poll();
if(tmp<n.depth) tmp=n.depth;
for(int d=0;d<4;d++){
int a=n.x+moves[d][0];
int b=n.y+moves[d][1];
if(a<0 || a>=N || b<0 || b>=M) continue;
if(mapNum[a][b]==cnt && !tmpV[a][b]){
queue.offer(new Node(a,b,n.depth+1));
tmpV[a][b]=true;
}
}
}
}
private static void bfs(int i, int j,int cnt) {
Queue<Point> queue=new ArrayDeque<>();
queue.offer(new Point(i,j));
visited[i][j]=true;
mapNum[i][j]=cnt;
while(!queue.isEmpty()){
Point p=queue.poll();
for(int d=0;d<4;d++){
int a=p.x+moves[d][0];
int b=p.y+moves[d][1];
if(a<0 || a>=N || b<0 || b>=M) continue;
if(map[a][b]=='L' && !visited[a][b]){
queue.offer(new Point(a,b));
visited[a][b]=true;
mapNum[a][b]=cnt;
}
}
}
}
}문제를 이해해보자면 육지 덩어리가 여러 개 나오게 되는데
각 육지 덩어리에 있는 육지들 중 가장 거리가 먼 육지들의 거리를 구하고
그 거리가 가장 큰 값을 구하는 것이다.
정리해보자면
- 육지 덩어리 내부에는 육지가 있다. 편의상 내부에 있는 육지 하나는 한 칸이라고 말하겠다.
- 육지 덩어리 내부에서 탐색을 진행했을 때 가장 먼 거리에 있는 칸을 찾고 그 거리를 구한다.
- 이때, 어느 칸에서 시작하는지에 따라 거리값이 달라지기 때문에 완전탐색을 통해 모든 칸들을 시작점으로 하여 거리를 구해본다.
- 각 육지 덩어리들 중 그 거리가 가장 큰 값을 출력한다.
그래프로 대입해서 얘기하자면 각 트리의 leaf node에서 다른 leaf node까지의 거리를 구해보는 것이다.
육지별로 번호 매기기
//main 함수
int cnt=1;
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
if(map[i][j]=='L' && !visited[i][j]){
bfs(i,j,cnt);
cnt++;
}
}
}
//bfs 탐색 함수
private static void bfs(int i, int j,int cnt) {
Queue<Point> queue=new ArrayDeque<>();
queue.offer(new Point(i,j));
visited[i][j]=true;
mapNum[i][j]=cnt;
while(!queue.isEmpty()){
Point p=queue.poll();
for(int d=0;d<4;d++){
int a=p.x+moves[d][0];
int b=p.y+moves[d][1];
if(a<0 || a>=N || b<0 || b>=M) continue;
if(map[a][b]=='L' && !visited[a][b]){
queue.offer(new Point(a,b));
visited[a][b]=true;
mapNum[a][b]=cnt;
}
}
}
}육지와 바다 정보가 들어있는 map 배열에서 육지이고 방문하지 않은 곳이라면 bfs 탐색을 진행하여 몇 번째 육지 덩어리인지 번호를 매겨준다.
이때 bfs 탐색은 평소에 자주 쓰는 bfs 탐색 코드를 이용해주고 mapNum이라는 배열에 해당 위치의 육지 자리에 육지 번호를 넣어준다.
즉, 첫번째로 발견한 육지 덩어리라면 그 칸과 이어져있는 육지들 모두에 1이라는 숫자를 넣어주는 것이다.
모든 탐색이 끝나면 이어져있는 칸들은 모두 방문한 것이기 때문에 다음 육지 덩어리를 위해 육지 번호를 증가시킨다.
각 육지 덩어리들에 번호를 매겨주었으니 이제 각 육지 내부에서 보물이 위치할 수 있는 칸들의 거리를 구해보자.
육지끼리의 거리 구하기
// 육지의 위치와 거리값 구하기위한 class
public static class Node{
int x,y,depth;
public Node(int x, int y, int depth) {
this.x = x;
this.y = y;
this.depth = depth;
}
}
//main 함수
for(int c=1;c<=cnt;c++){
for(int i=0;i<N;i++){
for(int j=0;j<M;j++){
tmp=0;
if(mapNum[i][j]==c){
bfsNum(i,j,c);
if(tmp>dist){
dist=tmp;
}
}
}
}
}우선, 상하좌우로 탐색을 하고 최단거리값을 구하기 위해 Node라는 class를 선언하여 사용했다.
x,y로 육지의 위치를 저장하고, depth에 시작점(탐색을 시작하는 육지)에서 해당 육지까지의 거리값이 들어갈 수 있는 변수를 선언했다.
그리고 육지 덩어리마다 최단거리를 모두 구해야하기 때문에 육지 덩어리를 모두 탐색하기 위한 for문 + 육지 덩어리 내부의 칸(육지) 완전탐색 for문을 써서 bfs 탐색을 진행한다.
tmp라는 임시 변수를 이용하여 해당 육지 덩어리에서 나온 최단거리 값을 넣어주고 최종적으로 출력하기위한 dist 변수와 비교하여 큰 값으로 갱신해준다.
즉, tmp는 한 육지 덩어리에서 나온 최단거리값이고, dist는 보물섬이 위치할 수 있는 가장 긴 최단거리값인 것이다.
두번째 bfs 탐색
//bfs 탐색2
private static void bfsNum(int i, int j, int cnt) {
boolean[][] tmpV=new boolean[N][M];
Queue<Node> queue=new ArrayDeque<>();
queue.offer(new Node(i,j,0));
tmpV[i][j]=true;
while(!queue.isEmpty()){
Node n=queue.poll();
if(tmp<n.depth) tmp=n.depth;
for(int d=0;d<4;d++){
int a=n.x+moves[d][0];
int b=n.y+moves[d][1];
if(a<0 || a>=N || b<0 || b>=M) continue;
if(mapNum[a][b]==cnt && !tmpV[a][b]){
queue.offer(new Node(a,b,n.depth+1));
tmpV[a][b]=true;
}
}
}
}각 육지 덩어리에서 나올 수 있는 최단거리값을 구해보는 bfs 탐색이다.
이전에 선언했던 Node class를 이용하여 큐에 값을 넣어준다.
탐색하고자 하는 육지 덩어리인 경우에만 탐색해야 하기 때문에 cnt라는 육지번호를 받아와 같은 육지 번호인 경우에만 탐색을 진행한다.
큐에 들어있는 값에서 거리값이 tmp라는 변수보다 크게 되면 tmp를 갱신하는 조건을 넣어주면 해당 육지에서 끝과 끝까지의 거리를 구할 수 있게 된다.
처음에 문제를 이해하지 못해서 여러번 다시 읽어보고 문제를 이해했다. 문제를 파악한 후에 차근차근 하나씩 로직을 짜고 코딩하니 금방 구현할 수 있었던 문제였다.
관건은 문제를 잘 이해하는 것이다.!
