문제
오늘은 스타트링크에 다니는 사람들이 모여서 축구를 해보려고 한다. 축구는 평일 오후에 하고 의무 참석도 아니다. 축구를 하기 위해 모인 사람은 총 N명이고 신기하게도 N은 짝수이다. 이제 N/2명으로 이루어진 스타트 팀과 링크 팀으로 사람들을 나눠야 한다.
BOJ를 운영하는 회사 답게 사람에게 번호를 1부터 N까지로 배정했고, 아래와 같은 능력치를 조사했다. 능력치 Sij는 i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치이다. 팀의 능력치는 팀에 속한 모든 쌍의 능력치 Sij의 합이다. Sij는 Sji와 다를 수도 있으며, i번 사람과 j번 사람이 같은 팀에 속했을 때, 팀에 더해지는 능력치는 Sij와 Sji이다.
N=4이고, S가 아래와 같은 경우를 살펴보자.
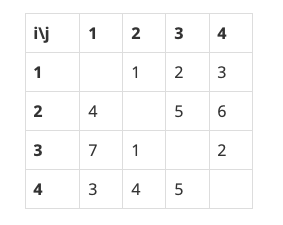
예를 들어, 1, 2번이 스타트 팀, 3, 4번이 링크 팀에 속한 경우에 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S12 + S21 = 1 + 4 = 5
- 링크 팀: S34 + S43 = 2 + 5 = 7
1, 3번이 스타트 팀, 2, 4번이 링크 팀에 속하면, 두 팀의 능력치는 아래와 같다.
- 스타트 팀: S13 + S31 = 2 + 7 = 9
- 링크 팀: S24 + S42 = 6 + 4 = 10
축구를 재미있게 하기 위해서 스타트 팀의 능력치와 링크 팀의 능력치의 차이를 최소로 하려고 한다. 위의 예제와 같은 경우에는 1, 4번이 스타트 팀, 2, 3번 팀이 링크 팀에 속하면 스타트 팀의 능력치는 6, 링크 팀의 능력치는 6이 되어서 차이가 0이 되고 이 값이 최소이다.
입력
첫째 줄에 N(4 ≤ N ≤ 20, N은 짝수)이 주어진다. 둘째 줄부터 N개의 줄에 S가 주어진다. 각 줄은 N개의 수로 이루어져 있고, i번 줄의 j번째 수는 Sij 이다. Sii는 항상 0이고, 나머지 Sij는 1보다 크거나 같고, 100보다 작거나 같은 정수이다.
출력
첫째 줄에 스타트 팀과 링크 팀의 능력치의 차이의 최솟값을 출력한다.
예제 입력 1
4
0 1 2 3
4 0 5 6
7 1 0 2
3 4 5 0예제 출력 1
0예제 입력 2
6
0 1 2 3 4 5
1 0 2 3 4 5
1 2 0 3 4 5
1 2 3 0 4 5
1 2 3 4 0 5
1 2 3 4 5 0예제 출력 2
2예제 입력 3
8
0 5 4 5 4 5 4 5
4 0 5 1 2 3 4 5
9 8 0 1 2 3 1 2
9 9 9 0 9 9 9 9
1 1 1 1 0 1 1 1
8 7 6 5 4 0 3 2
9 1 9 1 9 1 0 9
6 5 4 3 2 1 9 0예제 출력 3
1힌트
예제 2의 경우에 (1, 3, 6), (2, 4, 5)로 팀을 나누면 되고, 예제 3의 경우에는 (1, 2, 4, 5), (3, 6, 7, 8)로 팀을 나누면 된다.
문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BJ14889 {
static int[][] map;
static boolean[] selected;
static int N,result=Integer.MAX_VALUE;
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st;
N=Integer.parseInt(br.readLine());
map=new int[N][N];
selected=new boolean[N];
for(int i=0;i<N;i++){
st=new StringTokenizer(br.readLine());
for(int j=0;j<N;j++){
map[i][j]=Integer.parseInt(st.nextToken());
}
}
//조합
team(0,0);
System.out.println(result);
}
private static void team(int idx,int cnt) {
if(cnt==N/2){
int[] st=new int[N/2];
int[] link=new int[N/2];
int s=0,l=0;
for(int i=0;i<N;i++){
if(selected[i]){
st[s]=i;
s++;
}else{
link[l]=i;
l++;
}
}
//능력 계산
int a=cal(st);
int b=cal(link);
result=Math.min(result,Math.abs(a-b));
return;
}
for(int i=idx;i<N;i++){
selected[i]=true;
team(i+1,cnt+1);
selected[i]=false;
}
}
private static int cal(int[] team) {
int sum=0;
for(int i=0;i<N/2;i++){
int a=team[i];
for(int j=i;j<N/2;j++){
int b=team[j];
sum+=map[a][b]+map[b][a];
}
}
return sum;
}
}이전에 포스팅한 링크와 스타트 문제의 하위버전 문제이다.
링크와 스타트 문제는 각 팀에 몇 명이 있어야하는지 지정되어있지 않았기 때문에 부분집합을 이용하여 팀원을 지정해줬고
스타트와 링크 문제는 각 팀에 N/2명이 속하게 된다고 문제에서 지정했기 때문에 조합을 이용하여 각 팀에 N/2명을 만들어주면 된다.
팀원 나누기
private static void team(int idx,int cnt) {
if(cnt==N/2){
int[] st=new int[N/2];
int[] link=new int[N/2];
int s=0,l=0;
for(int i=0;i<N;i++){
if(selected[i]){
st[s]=i;
s++;
}else{
link[l]=i;
l++;
}
}
//능력 계산
int a=cal(st);
int b=cal(link);
result=Math.min(result,Math.abs(a-b));
return;
}
for(int i=idx;i<N;i++){
selected[i]=true;
team(i+1,cnt+1);
selected[i]=false;
}
}우선 조합 알고리즘을 이용하여 각 팀이 N/2명이 되도록 조합을 짜준다.
선택된 사람은 boolean 배열을 이용하여 true 처리를 해주고 재귀호출을 해준다.
재귀호출이 끝나고 return 되면 선택했던 사람은 false 처리를 해주고 다음 사람을 선택하기위해 반복문을 돌린다.
재귀의 횟수가 N/2가 되면 즉, 한 팀에 N/2명을 선택하게 되면 해당 조합의 경우에 각 팀의 팀원들의 능력치를 구하고 차이의 최소값을 갱신한다.
팀의 능력치 구하기
private static int cal(int[] team) {
int sum=0;
for(int i=0;i<N/2;i++){
int a=team[i];
for(int j=i;j<N/2;j++){
int b=team[j];
sum+=map[a][b]+map[b][a];
}
}
return sum;
}2중 for문을 이용하고 j변수의 시작을 i로 잡아주면 중복되지 않게 각 팀원의 능력치 합을 구할 수 있다.
즉, map[1][2]+map[2][1]+map[1][3]+map[3][1]+map[2][3]+map[3][2] 처럼 능력치를 구해야하는 상황이라면
반복문의 순서대로 map[1][2]+map[1][3]+map[2][3] 을 구하고 각 경우에 i와 j의 위치를 바꾼 값도 더해주게 되면 원하는 결과를 얻을 수 있다.
합한 능력치의 값을 return 해주면 team 메소드에서 이를 받아 최소값을 갱신하여 답을 도출할 수 있게 된다.
이전 포스팅
링크와 스타트 - 자바 풀이
