문제
컴공 출신은 치킨집을 하게 되어있다. 현실을 부정하지 말고 받아들이면 마음이 편하다. 결국 호석이도 2050년에는 치킨집을 하고 있다. 치킨집 이름은 "호석이 두마리 치킨"이다.
이번에 키친 도시로 분점을 확보하게 된 호석이 두마리 치킨은 도시 안에 2개의 매장을 지으려고 한다. 도시는 N 개의 건물과 M 개의 도로로 이루어져 있다. 건물은 1번부터 N번의 번호를 가지고 있다. i 번째 도로는 서로 다른 두 건물 Ai 번과 Bi 번 사이를 1 시간에 양방향으로 이동할 수 있는 도로이다.
키친 도시에서 2개의 건물을 골라서 치킨집을 열려고 한다. 이 때 아무 곳이나 열 순 없어서 모든 건물에서의 접근성의 합을 최소화하려고 한다. 건물 X 의 접근성은 X 에서 가장 가까운 호석이 두마리 치킨집까지 왕복하는 최단 시간이다. 즉, "모든 건물에서 가장 가까운 치킨집까지 왕복하는 최단 시간의 총합"을 최소화할 수 있는 건물 2개를 골라서 치킨집을 열려고 하는 것이다.
컴공을 졸업한 지 30년이 넘어가는 호석이는 이제 코딩으로 이 문제를 해결할 줄 모른다. 알고리즘 퇴물 호석이를 위해서 최적의 위치가 될 수 있는 건물 2개의 번호와 그 때의 "모든 건물에서 가장 가까운 치킨집까지 왕복하는 최단 시간의 총합"을 출력하자. 만약 이러한 건물 조합이 여러 개라면, 건물 번호 중 작은 게 더 작을수록, 작은 번호가 같다면 큰 번호가 더 작을수록 좋은 건물 조합이다.
입력
첫 번째 줄에 건물의 개수 N과 도로의 개수 M 이 주어진다. 이어서 M 개의 줄에 걸쳐서 도로의 정보 Ai , Bi 가 공백으로 나뉘어서 주어진다. 같은 도로가 중복되어 주어지는 경우는 없다. 어떤 두 건물을 잡아도 도로를 따라서 오고 가는 방법이 존재함이 보장된다.
출력
한 줄에 건물 2개가 지어질 건물 번호를 오름차순으로 출력하고, 그때 모든 도시에서의 왕복 시간의 합을 출력한다.
만약 건물 조합이 다양하게 가능하면, 작은 번호가 더 작은 것을, 작은 번호가 같다면 큰 번호가 더 작은 걸 출력한다.
제한
2 ≤ N ≤ 100
N-1 ≤ M ≤ N×(N - 1)/2
1 ≤ Ai , Bi ≤ N (Ai ≠ Bi)
예제 입력 1
5 4
1 3
4 2
2 5
3 2예제 출력 1
1 2 6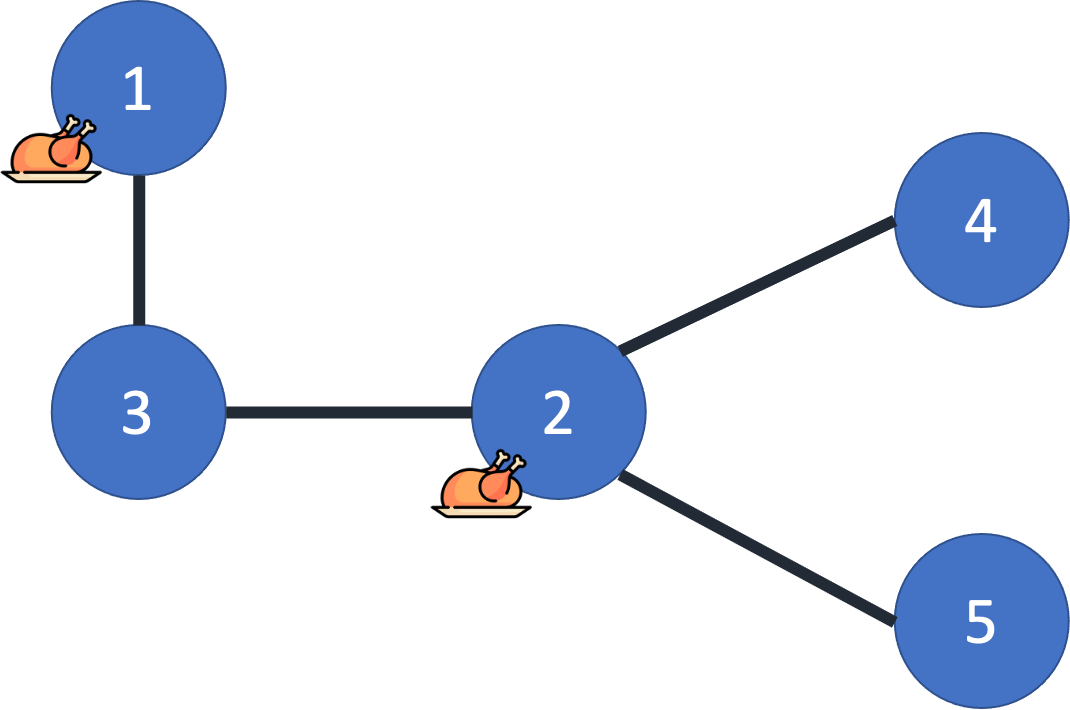
위의 그림과 같이 1번과 2번 건물에 치킨집을 짓게 되면 1번부터 5번 건물에 대해 치킨집까지의 왕복 시간이 0, 0, 2, 2, 2 로 최소가 된다. 2번과 3번 건물에 지어도 동일한 왕복 시간이 나오지만 더 작은 건물 번호를 출력해야 함을 유의하자.
문제 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class BJ21278 {
static int[][] map;
static int N,M;
static boolean[] visited;
static int tmp,a,b;
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
N=Integer.parseInt(st.nextToken());
M=Integer.parseInt(st.nextToken());
map=new int[N][N];
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
map[i][j]=(int)1e9;
}
}
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int a=Integer.parseInt(st.nextToken())-1;
int b=Integer.parseInt(st.nextToken())-1;
map[a][b]=1;
map[b][a]=1;
}
for(int k=0;k<N;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
if(i==j || j==k || k==i) continue;
if(map[i][j]>map[i][k]+map[k][j]){
map[i][j]=map[i][k]+map[k][j];
}
}
}
}
int result=Integer.MAX_VALUE;
// 치킨 집 두 곳 지정
for(int i=0;i<N;i++){
for(int j=i+1;j<N;j++){
tmp=0;
for(int k=0;k<N;k++){
if(i==k || j==k) continue;
int min=Math.min(map[i][k],map[j][k]);
tmp+=min;
}
if(tmp<result){
result=tmp;
a=i+1;
b=j+1;
}
}
}
System.out.println(a+" "+b+" "+result*2);
}
}치킨집 두 군데를 지정한 다음 근처 건물에서 왕복하는 시간 합의 최소값을 구하는 문제였다.
플로이드 워셜을 이용하여 각 노드에서 다른 노드까지의 거리값을 미리 구해준 다음 치킨집 두 곳을 지정하여 왕복하는데 걸리는 최소시간을 구하는 방식을 이용한다.
플로이드 워셜을 이용하여 최소 거리값 구해주기
map=new int[N][N];
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
map[i][j]=(int)1e9;
}
}
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int a=Integer.parseInt(st.nextToken())-1;
int b=Integer.parseInt(st.nextToken())-1;
map[a][b]=1;
map[b][a]=1;
}
for(int k=0;k<N;k++){
for(int i=0;i<N;i++){
for(int j=0;j<N;j++){
if(i==j || j==k || k==i) continue;
if(map[i][j]>map[i][k]+map[k][j]){
map[i][j]=map[i][k]+map[k][j];
}
}
}
}map 배열에 1e9라는 큰 값으로 초기화해준다.
입력값을 통해 이어진 노드들은 1로 설정해주고 플로이드워셜을 통해 최소거리값을 갱신한다.
k 변수는 거쳐갈 정점을 나타내는 것으로
예를 들어, 1번 -> 2번 노드로 향하는 값이 5이고, 1번 -> 3번 -> 2번 처럼 3번 노드를 거쳐서 가는 경우 거리값이 3이라고 한다면 1번에서 2번으로 향하는 최소거리값은 3이 된다.
위 예시를 그대로 코드로 구현한 것이 플로이드 워셜이다.
k변수를 3번과 같은 거쳐갈 정점, i는 1번과 같이 출발하는 정점, j는 2번과 같이 도착할 정점을 나타낸다.
만약 1번에서 2번으로 향하는 거리값인 map[i][j]보다 3번을 거쳐서 도달하는 map[i][k]+map[k][j] 거리값이 더 적다면 map[i][j]값을 갱신해주는 것이다.
모든 작업을 마무리하면 각 노드로 향하는 최소거리값이 구해진다.
치킨가게 두 곳 지정하여 최소값 구하기
int result=Integer.MAX_VALUE;
// 치킨 집 두 곳 지정
for(int i=0;i<N;i++){
for(int j=i+1;j<N;j++){
tmp=0;
for(int k=0;k<N;k++){
if(i==k || j==k) continue;
int min=Math.min(map[i][k],map[j][k]);
tmp+=min;
}
if(tmp<result){
result=tmp;
a=i+1;
b=j+1;
}
}
}치킨집은 두 곳으로 정해져있기 때문에 완전탐색을 통해 치킨집 두 곳을 지정한다.
(1번, 2번), (2번, 1번) 을 치킨집으로 지정하는것은 결국 같은 결과이기 때문에 j=i+1으로 반복문 변수를 초기화해준다.
치킨집 두 곳을 지정했다면 모든 노드에서 치킨집까지 도달하는 거리값을 합해야하기 때문에 반복문을 한 번 더 사용해준다.
첫번째 치킨집과 두번째 치킨집 중 더 가까운 거리값을 tmp 변수에 추가해주고
모든 노드의 거리값이 추가되었다면 최종 결과 출력을 위해 result 변수와 비교해주고 값을 갱신해준다.
위 로직들을 반복해주면 답을 출력할 수 있다.
처음엔 치킨집 두 곳을 먼저 지정한 다음 BFS를 통해 모든 노드에 대해 최소거리값을 구할 생각이었는데 시간초과가 발생했다.
시간초과 발생 풀이
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.ArrayDeque;
import java.util.Queue;
import java.util.StringTokenizer;
public class Main {
static int[][] map;
static int N,M;
static boolean[] visited;
static int tmp;
static int a,b,min=Integer.MAX_VALUE;
public static class Node{
int node,dist;
public Node(int node, int dist) {
this.node = node;
this.dist = dist;
}
}
public static void main(String[] args) throws IOException {
BufferedReader br=new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st=new StringTokenizer(br.readLine());
N=Integer.parseInt(st.nextToken());
M=Integer.parseInt(st.nextToken());
map=new int[N][N];
for(int i=0;i<M;i++){
st=new StringTokenizer(br.readLine());
int a=Integer.parseInt(st.nextToken())-1;
int b=Integer.parseInt(st.nextToken())-1;
map[a][b]=1;
map[b][a]=1;
}
// 치킨 집 두 곳 지정
for(int i=0;i<N;i++){
for(int j=i;j<N;j++){
if(i==j) continue;
tmp=0;
for(int n=0;n<N;n++) {
tmp+=bfs(i, j,n);
}
if(tmp<min){
min=tmp;
a=i+1;
b=j+1;
}
}
}
System.out.println(a+" "+b+" "+min);
}
private static int bfs(int i, int j,int node) {
Queue<Node> queue=new ArrayDeque<>();
queue.offer(new Node(node,0));
visited=new boolean[N];
visited[node]=true;
int result=0;
while(!queue.isEmpty()){
Node n=queue.poll();
result=Math.max(result,n.dist);
if(n.node==i || n.node==j) break;
visited[n.node]=true;
for(int a=0;a<N;a++){
if(map[n.node][a]==1 && !visited[a]){
queue.offer(new Node(a,n.dist+1));
}
}
}
return result*2;
}
}시간초과를 없애기 위해 구글링을 하던 중 치킨집 두 곳을 먼저 구하지 말고 거리값을 먼저 구한 뒤 치킨집 위치를 구하는 방식이 시간초과가 발생하지 않는다는 힌트를 얻고
플로이드 워셜을 이용하여 문제를 풀었고 빠른 속도로 정답처리가 되었다.

