1. 벨만포드 알고리즘 정리
벤만포드(Bellman-Ford) 알고리즘은 다익스트라가 처리 못하는 음의 가중치(negative weight)가 있는 그래프에서 최단 경로를 구할 수 있는 알고리즘이다
제약 조건은 negative cycle이 있으면 안된다
여기서 negative cycle을 이해하기 위해서는 아래 그림을 보면 된다
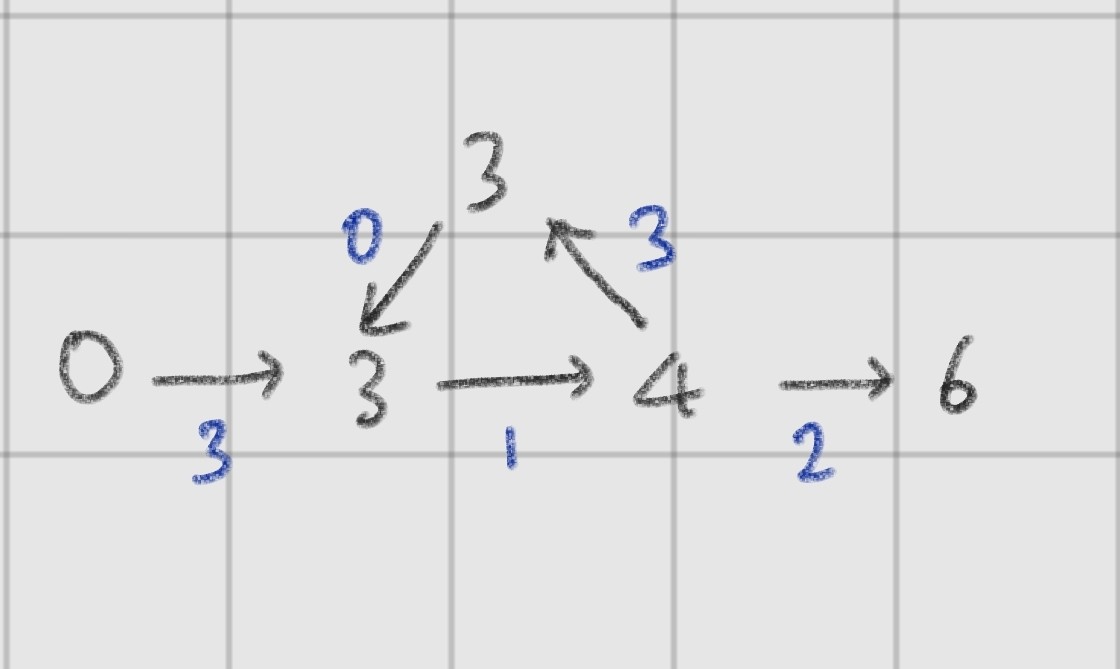위 그림을 보고 최단 경로를 구하면 0->3->4->6으로 이동하면 되고 다익스트라를 사용해서 충분히 풀 수 있다
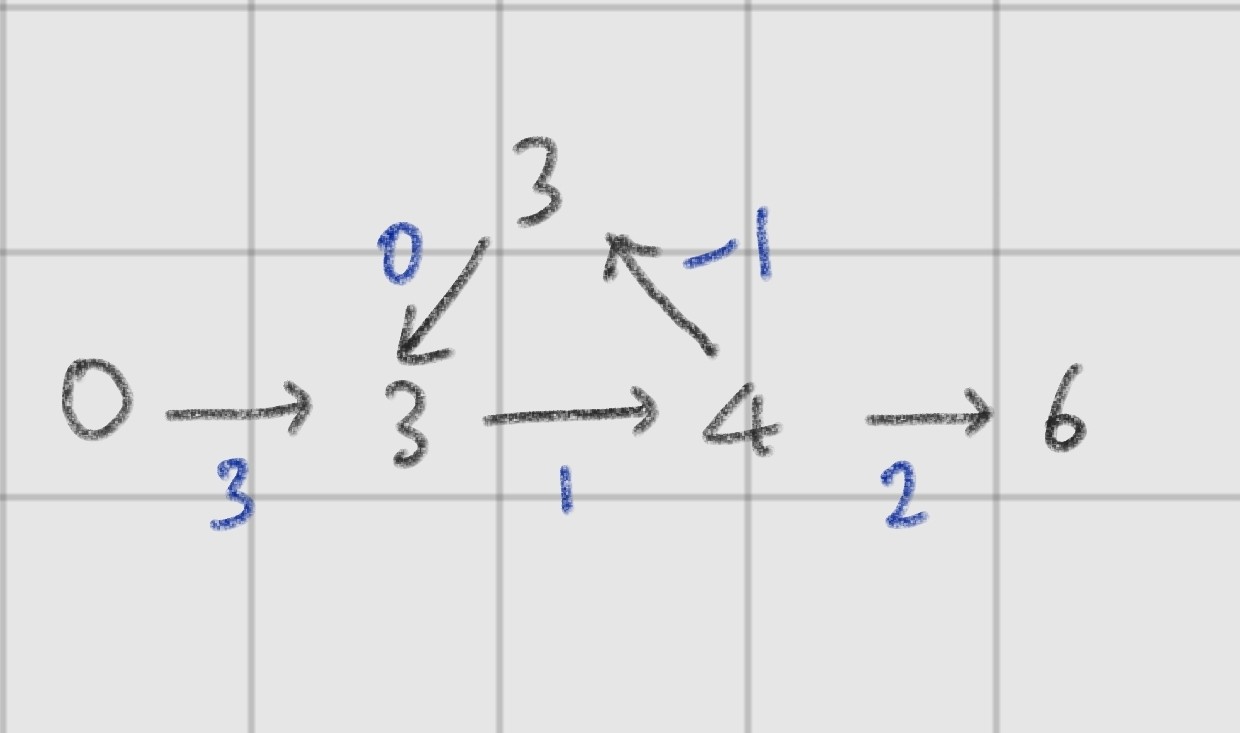위 그림은 다익스트라로 사용은 못하고 벨만포드를 사용해야 한다
또한 3->4->3 이 부분을 계속 돌게 되는 사이클이 발생하는데 이는 가중치의 합이 변하지도 않고 해당 정점에 몇 번까지 방문할 수 있는지 제한을 걸어두면 되기 때문에 nagative cycle이 아니다
제한을 걸어두는 방법은 그래프의 정점의 개수를 v라고 할 때 인접 간선을 검사하고 거리 값을 갱신하는 과정을 v−1번으로 제한하면 된다
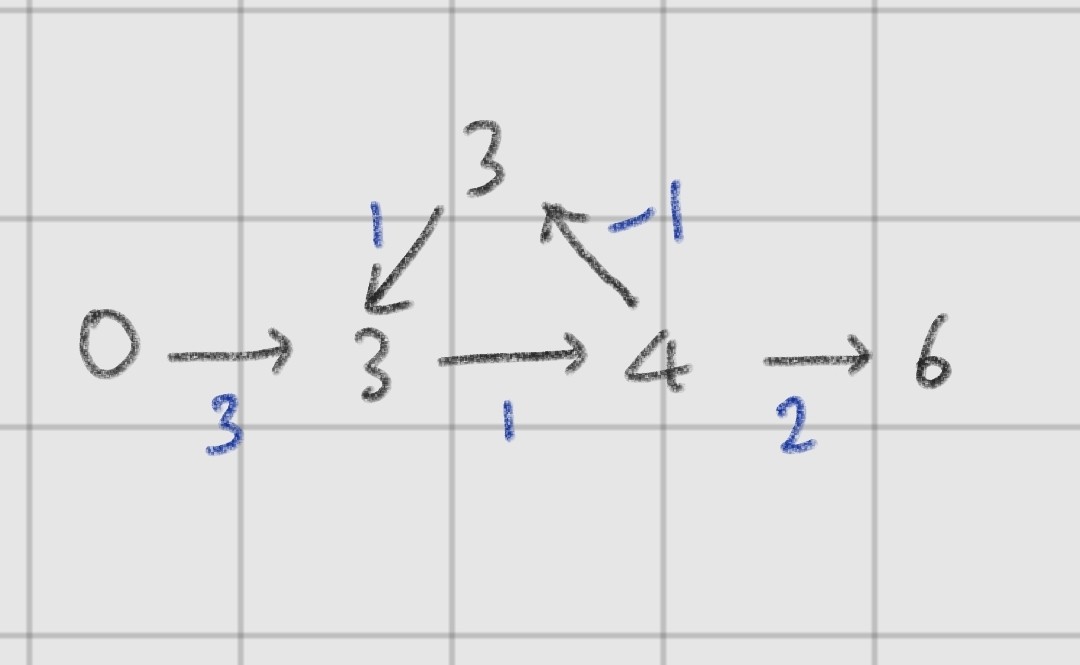위 그림을 보면 앞선 그림과 같이 3->4->3 부분을 돌게 되는 사이클이 발생한다
하지만 앞선 예시와는 달리 사이클이 돌면 돌수록 가중치 합의 값이 달라지게 된다
이를 nagative cycle이라고 한다
nagative cycle이 발생하게 되면 벨만포드로 문제를 풀이할 수 없다
수업시간에 배운 코드를 이용해서 벨만 포드 알고리즘을 구현하자면
#include <iostream>
#include <vector>
#include <climits>
#include <fstream>
using namespace std;
struct Edge {
int src; //시작점
int dst; //끝점
int weight; //가중치
};
const int UNKOWN = INT_MAX; //초기화 시키기
bool ReadTestCase(string filename, int& N, vector<Edge>& edges) { //txt파일 가져오는거
ifstream infile(filename);
if (!infile.is_open()) {
cout << "error" << endl;
return false; //못가져오면 에러메시지 뜨도록
}
infile >> N;
for (int i = 0; i < N * N - 1; i++) { //예시는 3*3 총 9개임
string directions; //방향
int power; //베터리
infile >> directions >> power;
int next = i;
for (auto d : directions){
switch (d) { //움직인 만큼 셀의 크기 만큼 줄어들기
case 'N': next = i - N; break; //북쪽으로 가면 n만큼 줄이기
case 'E': next = i + 1; break;
case 'S': next = i + N; break;
case 'W': next = i - 1; break;
}
edges.push_back(Edge {i, next, -power}); //power에 -붙이는거 잊지 말기
}
}
return true;
}
vector<int> BellmanFord(vector<Edge> edges, int V, int start) { //벨만코드 알고리즘 그대로 가져온거
vector<int> distance(V, UNKOWN);
distance[start] = 0;
for (int i = 0; i < V - 1; ++i) {
for (auto& e : edges) {
if (distance[e.src] == UNKOWN)
continue;
if (distance[e.dst] > distance[e.src] + e.weight)
distance[e.dst] = distance[e.src] + e.weight;
}
}
return distance;
}
int main() {
int N;
vector<Edge> edges;
if (ReadTestCase("testcase1.txt", N, edges)) //파일이름. 갯수, 간선
{
vector<int> distance = BellmanFord(edges, N * N, 0); //셀이 9개 있다(정점의 갯수 = n*n)
if (distance.empty() || distance[N * N - 1] == UNKOWN)
cout << "탐색 중단" << endl;
else
cout << -1 * distance[N * N - 1] << endl; //-1을 쓴 이유는 벨만코드는 최소값을 구하는거니까 최대값을 구하기 위해 -1을 곱해 부호를 바꿔서 진행하도록 한다
}
}2. Leet code 문제 풀이
Leet code 743번: 네트워크 딜레이 시간
https://leetcode.com/problems/network-delay-time/
2.1. 다익스트라를 이용한 풀이
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
vector<int> res(N+1, -1);
unordered_map<int, vector<pair<int,int>> > mp;
for(auto t : times){
mp[t[0]].push_back({t[1], t[2]});
}
int longest = 0;
int count = 1;
res[K] = 0;
queue<int> q;
q.push(K);
while(!q.empty()){
int source = q.front();
q.pop();
for(auto p : mp[source]){
if(res[p.first] == -1 || res[p.first] > p.second + res[source]){
if(res[p.first] == -1) count++;
res[p.first] = p.second + res[source];
q.push(p.first);
}
}
}
if(count != N) return -1;
for(int i = 1; i < res.size(); ++i){
longest = max(longest, res[i]);
}
return longest;
}
};2.2. 벨만포드를 이용한 풀이
class Solution {
public:
int networkDelayTime(vector<vector<int>>& times, int N, int K) {
constexpr int MAX_TIME = 101 * 100;
vector<int> dist(N, MAX_TIME);
dist[K - 1] = 0;
for (int i = 1; i < N; ++i)
for (const auto& time : times) {
int u = time[0] - 1, v = time[1] - 1, w = time[2];
dist[v] = min(dist[v], dist[u] + w);
}
int max_dist = *max_element(dist.begin(), dist.end());
return max_dist == MAX_TIME ? -1 : max_dist;
}
};3. 백준 문제 풀이
백준 1916번: 최소비용 구하기https://www.acmicpc.net/problem/1916
3.1. 다익스트라를 이용한 풀이
#include <iostream>
#include <vector>
#include <algorithm>
#include <queue>
#define INF 987654321
using namespace std;
int dist[1001];
vector<pair<int, int>> vec[100001];
void dijkstra(int start) {
dist[start] = 0; // 처음 위치는 0
priority_queue<pair<int, int>>pq;
pq.push({ dist[start] , start });
while (!pq.empty()) {
int cur = pq.top().second; // 큐의 가장 맨 앞에 있는 정점의 번호를 담아온다.
int distance = pq.top().first * -1;
pq.pop();
// 이미 담겨 있는 것보다 distance가 크면 넘어간다.
if (dist[cur] < distance) continue;
// 선택한 노드의 모든 인접 노드들을 확인한다.
for (int i = 0; i < vec[cur].size(); i++) {
int next = vec[cur][i].first;
int nextDistance = distance + vec[cur][i].second;
// 다음 것과 기존의 비용과 비교
if (nextDistance < dist[next]) {
dist[next] = nextDistance;
pq.push({nextDistance * -1 , next});
}
}
}
}
int main() {
ios::sync_with_stdio(0);
cin.tie(0);
int start, end;
int N, M;
cin >> N; // 정점 갯수
cin >> M; // 간선 갯수
for (int i = 1; i <= N; i++)
dist[i] = INF;
for (int i = 0; i < M; i++) {
int u, v, w;
cin >> u >> v >> w;
vec[u].push_back({ v,w });
}
cin >> start; // 시작점
cin >> end; // 도착점
dijkstra(start);
cout << dist[end];
return 0;
}3.2. 벨만포드를 이용한 풀이
#include <iostream>
#include <vector>
#define INF 99999999
using namespace std;
int V,M;
vector<pair<int, int> > v[1001];
int upper[1001];
int bellmanFord(int src) { //시작점 제외 모든 정점까지의 최단거리 INF로 초기화
fill_n(upper, 1001, INF);
upper[src] = 0;
bool updated;
for(int i = 0; i < V; i++) {
updated = false;
for(int j = 1; j <= V; j++)
for(int k = 0; k < v[j].size(); k++) {
int there = v[j][k].first;
int cost = v[j][k].second;
if(upper[there] > upper[j] + cost) { // 완화 성공
upper[there] = upper[j] + cost;
updated = true;
}
}
if(!updated) break; //모든 간선에 대해 완화가 실패할경우 break;
}
if(updated) return 1; //음수 사이클이 존재
return 0;
}
int main(void) {
cin >> V >> M;
for(int i = 0; i < M; i++) {
int a,b,c;
cin >> a >> b >> c;
v[a].push_back(make_pair(b, c));
}
int start, arrive; cin >> start >> arrive;
if(!bellmanFord(start))
cout<<upper[arrive];
return 0;
}위의 문제 풀이를 하면서 도움을 받은 곳들이다
https://leetcode.com/problems/network-delay-time/solutions/109988/743-network-delay-time-c-ac_bfs_like-dijkstras-algorithm/
https://zxi.mytechroad.com/blog/graph/leetcode-743-network-delay-time/
https://chanhuiseok.github.io/posts/baek-15/
https://huiung.tistory.com/106
배운 내용 적어보는 중