
이진 탐색 트리(Binary Search Tree)
이진 트리 중에서 왼쪽에는 부모 노드보다 작은 값이 오고, 오른쪽에는 부모 노드보다 큰 값이 오는 트리를 이진 탐색 트리 라고 한다.
탐색 연산
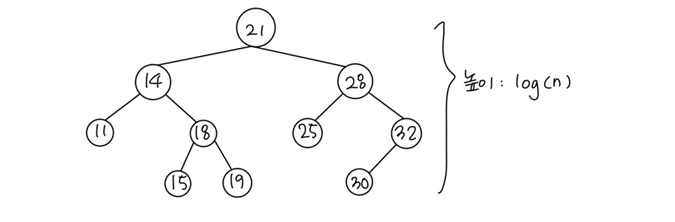
이진 탐색 트리를 중위 순회하면 11 - 14 - 15 - 18 - 19 - 21 - 25 - 28 - 30 - 32로 숫자들의 크기순이 된다. 이진 탐색 트리가 어느 정도 정렬된 상태를 유지하고 있음을 보여준다.
이진 탐색 트리는 숫자 크기 순서대로 정렬되어 있기 때문에 특정 노드를 검색할 때 작으면 왼쪽 절반을 탐색하고, 크면 오른쪽 절반을 탐색한다. 트리에 n개의 노드가 있을 때, 특정 노드를 검색하는 데는 트리의 높이만큼인 log(n)의 시간이 걸린다.
class Node:
def __init__(self, data):
self.data = data
self.left = None
self.right = None이진 트리를 구현할 때와 마찬가지로 노드는 값, 왼쪽 에지, 오른쪽 에지로 구성된다.
class BinarySearchTree():
def __init__(self):
self.root = None
def search(self, key):
return self._search_value(self.root, key)
def _search_value(self, root, key):
if root is None or root.data == key:
return root is not None
elif key < root.data:
return self._search_value(root.left, key)
else:
return self._search_value(root.right, key)
_search_value()함수는 삽입이 완료된 루트노드에서 key값(검색할 노드)을 찾는다.
루트노드에 값이 없거나 key값을 찾으면 반환한다.
key값이 부모 노드보다 작으면 왼쪽을 탐색하고, key값이 부모 노드보다 크면 오른쪽을 탐색한다.
삽입 연산
노드를 삽입하는 데는 삽입할 위치를 검색하는 시간 log(n)이 걸린다. 이진 탐색 트리의 삽입 연산을 구현한 코드는 아래와 같다.
class BinarySearchTree():
def insert(self, data):
self.root = self._insert_value(self.root, data)
return self.root is not None
def _insert_value(self, node, data):
if node is None:
node = Node(data)
else:
if data <= node.data:
node.left = self._insert_value(node.left, data)
else:
node.right = self._insert_value(node.right, data)
return node
insert()함수는 노드 1개씩 data를 받아_insert_value()함수를 실행한 뒤 값을 넣었으면True를 반환한다.
부모 노드가 비어있으면 부모 노드에 추가하고, 부모 노드에 값이 이미 들어있으면 자식 노드에 추가한다.
자식 노드에 추가할 때 부모 노드보다 작으면 왼쪽에 추가하고, 부모 노드보다 크면 오른쪽에 추가한다.
삭제 연산
이진 탐색 트리에서 특정 노드를 삭제할 때는 3가지 경우가 있다.
- 1) 삭제하려는 노드가 단말 노드인 경우
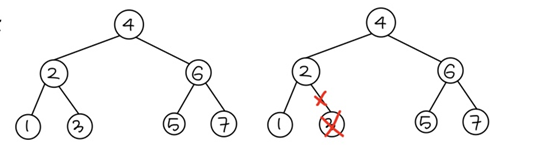
단말 노드를 삭제할 때는 부모노드의 링크를 끊으면 된다. 노드 3을 삭제하려면 노드 2 -> 노드 3의 링크를 끊는다.
- 2) 삭제하려는 노드가 서브 트리를 1개 가지는 경우

자기 노드는 삭제하고 자기 노드의 부모 노드가 서브 트리를 가리키도록 한다. 노드 2를 삭제하려면 노드 4 -> 노드 2의 링크를 끊고, 노드 4 -> 노드 1을 연결한다.
- 3) 삭제하려는 노드가 서브 트리를 2개 가지는 경우
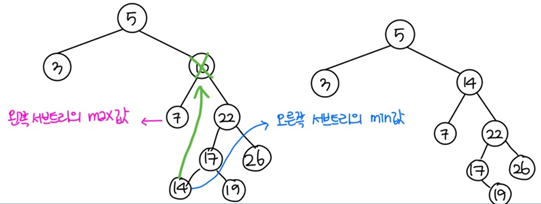
노드 10을 삭제하고 노드 10의 자식 노드인 7이나 22를 그대로 연결하면 이진 탄색 트리의 조건을 만족하지 않는다. 노드 10과 가장 가까운 값은 왼쪽 서브 트리의 가장 큰 값(노드 7) 이나 오른쪽 서브 트리의 가장 작은 값(노드 14)이다.
삭제한 노드 10에 노드 7 또는 노드 14 중 아무거나 넣어도 상관이 없다. 여기서는 큰 값인 노드 14를 넣기로 한다.
왼쪽 서브 트리의 가장 작은 값은 왼쪽 자식을 타고 내려가다가 왼쪽 자식이 NULL인 노드, 오른쪽 서브 트리의 가장 큰 값은 오른쪽 자식을 타고 내려가다가 오른쪽 자식이 NULL인 노드이다.
class BinarySearchTree():
def delete(self, key):
self.root, deleted = self._delete_value(self.root, key)
return deleted
def _delete_value(self, node, key):
# 노드가 비어있으면 False 반환
if node is None:
return node, False
deleted = False # flag 선언
# 삭제할 값을 찾은 경우
if key == node.data:
deleted = True
# 자식노드가 2개인 경우
if node.right and node.left:
# 오른쪽 서브트리의 가장 왼쪽 노드와 삭제할 노드를 바꾸기
parent, child = node, node.right
# 왼쪽 자식 노드를 탐색해 가장 작은값 찾기
while child.left is not None:
parent, child = child, child.left
child.left = node.left
if parent != node:
parent.left = child.right
child.left = node.right
child.right = node.right
node = child
# 자식노드가 1개인 경우
elif node.right or node.left:
node = node.right or node.left
# 자식노드가 없는 경우
else:
node = None
# 삭제할 값이 부모 노드보다 작은 경우
elif key <= node.data:
node.left, deleted = self._delete_value(node.left, key)
# 삭제할 값이 부모 노드보다 큰 경우
else:
node.right, deleted = self._delete_value(node.right, key)
return node, deleted전체 코드는 github에 있습니다.
