이진 트리 (Binary Tree)

트리는 계층적인 자료를 표현하는데 사용되는 자료 구조로, 노드의 자식이 최대 2개인 트리를 이진트리라고 한다.

트리의 개념

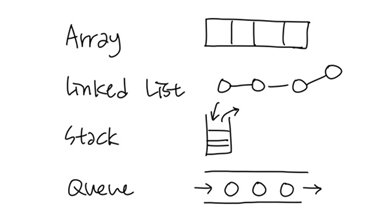
이전까지 다룬 자료 구조인 배열(Array), 연결 리스트(Linked List), 스택(Stack), 큐(Queue) 모두 직선과 같이 나열된 구조로, 선형 자료 구조에 해당한다.

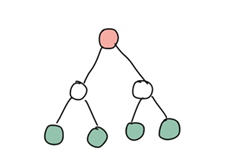
반면, 트리는 부모와 자식 관계를 가지는 구조로 계층적인 자료를 표현하는데 사용되는 자료 구조이다.

트리는 노드(node)와 에지(edge)로 구성되는데 위의 그림에서 동그라미가 노드, 선이 에지에 해당한다. 흰색 노드는 초록색 노드의 부모 노드가 되며, 반대로 초록색 노드는 흰색 노드의 자식 노드가 된다.

트리의 맨 위에 있는 빨간색 노드를 루트 노드(root node)라 하고, 자식이 없는 초록색 노드를 단말 노드(leaf node)라 한다.
(leaf node라서 초록색으로 칠해봤다 🍀)

이진 트리의 종류

이진 트리(Binary Tree)

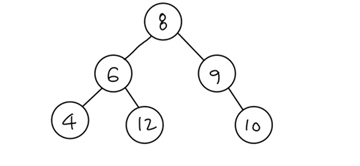
노드의 자식이 최대 2개인 트리를 이진트리 라고 한다.

이진 탐색 트리(Binary Search Tree)

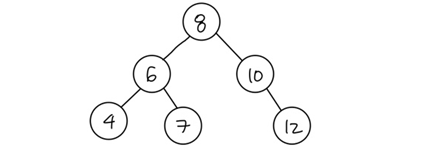
이진 트리 중에서 왼쪽에는 부모 노드보다 작은 값이 오고, 오른쪽에는 부모 노드보다 큰 값이 오는 트리를 이진 탐색 트리 라고 한다.
이러한 이진 탐색 트리의 특징을 이용해 탐색하려는 값이 현재 노드의 값보다 작으면 왼쪽을, 크면 오른쪽을 탐색하면 된다.

완전 이진 트리(Complete Binary Tree)

모든 노드들이 레벨별로 왼쪽부터 채워진 트리를 완전 이진 트리 라고 한다.

이진 트리의 3가지 순회 방법

• 이진 트리를 순회한다는 것은 이진 트리에 속하는 모든 노드를 한 번씩 방문해 노드가 가지고 있는 데이터를 목적에 맞게 처리하는 것을 의미한다.
• 이진 트리를 순회하는 방법에는 전위, 중위, 후위 3가지 방법이 있다. 루트, 왼쪽 서브 트리, 오른쪽 서브 트리 중에서 루트를 언제 방문하느냐에 따라 구분된다.

전위 순회(Preorder Traversal)
root - left - right
① - ② - ④ - ⑤ - ③

중위 순회(Inorder Traversal)
left - root - right
④ - ② - ⑤ - ① - ③

후위 순회(Postorder Traversal)
left - right - root
④ - ⑤ - ② - ③ - ①

구현

class Node:
    def __init__(self, data):
        self.data = data
        self.left = None
        self.right = None

트리는 데이터가 들어있는 노드와 오른쪽, 왼쪽 노드와 연결하는 에지로 구성된다.
해당 노드의 자식이 없을 수도 있기 때문에 self.left와 self.right는 None으로 선언한다.

class BinaryTree():
    def __init__(self):  # 트리 생성
        self.root = None

    def preorder(self, n):
        if n != None:
            print(n.data, ' ', end="")  # 루트노드 방문
            if n.left:
                self.preorder(n.left)  # 왼쪽 서브트리 순회
            if n.right:
                self.preorder(n.right)  # 오른쪽 서브트리 순회

전위 순회
루트 노드가 비어있지 않으면(값이 있으면) 순회를 시작한다.
루트 노드의 왼쪽 서브트리가 있으면, 왼쪽 서브트리를 순회한다.
마찬가지로 루트 노드의 오른쪽 서브트리가 있으면, 오른쪽 서브트리를 순회한다.

 def inorder(self, n):
    if n!= None:
        if n.left:
            self.inorder(n.left)  # 왼쪽 서브트리 순회
        print(n.data, ' ', end="")  # 루트노드 방문
        if n.right:
            self.inorder(n.right)  # 오른쪽 서브트리 순회

중위 순회
루트 노드가 비어있지 않으면 순회를 시작하며, 왼쪽 서브트리 -> 루트 노드 -> 오른쪽 서브 트리 순서로 순회한다.

def postorder(self, n):
    if n!= None:
        if n.left:
            self.postorder(n.left)  # 왼쪽 서브트리 순회
        if n.right:
            self.postorder(n.right)  # 오른쪽 서브트리 순회
        print(n.data, ' ', end="")  # 루트노드 방문

후위 순회
루트 노드가 비어있지 않으면 순회를 시작하며, 왼쪽 서브트리 -> 오른쪽 서브 트리 -> 루트 노드 순서로 순회한다.

def height(self, root):
    if root == None:
        return 0
    return max(self.height(root.left), self.height(root.right)) + 1

트리의 높이(레벨) 구하기
트리의 높이는 왼쪽 서브 트리, 오른쪽 서브 트리 중 높은 레벨을 의미한다.
루트의 레벨이 1이 되기 때문에 왼쪽 서브 트리의 높이와 오른쪽 서브 트리의 높이 중 큰 값을 구한 뒤에 1을 더한다.

전체 코드는 github에 있습니다.

References
엔지니어대한민국