gpt에 NumPy 배열의 구조를 잘 알려주는 자료를 달라고 하니 다음 논문을 알려줬다.
Harris, C. R., Millman, K. J., van der Walt, S. J., et al. (2020). Array programming with NumPy. Nature, 585, 357–362.
슬쩍 보니까 과학계에서 NumPy배열이 의미있게 쓰일 수 있다는 얘기를 하면서 NumPy배열에 대해 살짝 얘기해주고 있다.
사실 공식문서를 보는 것이 더 정보는 많을 것 같지만, 권위있는 Nature지에 실려있으면서, 멋진 석학들이 정리해둔 내용을 보는 것도 나쁘지 않을 것 같아서서, 멋진 학자들이 정리해둔 내용을 보는 것도 나쁘지 않을 것 같아서 해당 논문을 참조할 것이다.
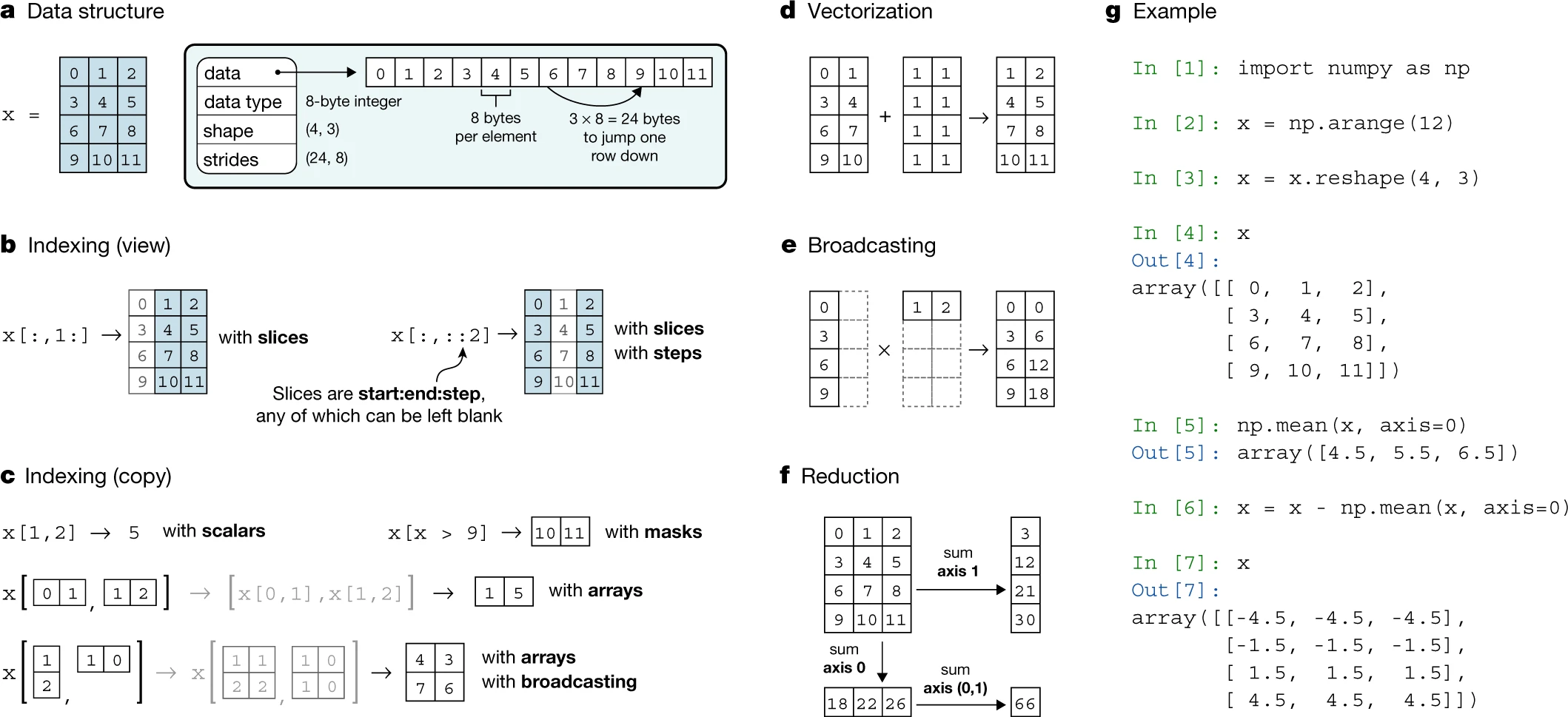
내가 보고싶은 NumPy배열의 동작이 나온 부분의 이미지다.
먼저 브로드캐스팅(broadcasting)이라는 내용을 알아야 할 것 같아서 구글링을 해봤다.
brocasting은 NumPy가 다른 shape의 배열을 처리하는 방식이다.
[출처, numpy.org]
shape는 배열의 모양이다.
1차원 텐서 = 배열 = 1행 n열 행렬
위 배열은 NumPy에서 아래와 같이 표현된다.
(n,) # 1차원 배열 형식
(1, n) # 2차원 배열 형식
1차원 배열의 경우 (열(원소개수),)로 나타내고, 2차원 배열은 (행, 열), 3차원 배열은 (층, 행, 열)로 나타낸다.
더 높은 차원도 표현할 수 있다.
다시 돌아와서 broadcasting은 NumPy가 서로 다른 shape를 가진 배열을 산술적으로 연산할 때
처리하는 방식이라고 했다.
공식문서에 따르면 두 개의 배열에서 작업할 때 가장 뒷쪽에 있는 차원부터 앞에 있는 차원 순서대로 작업한다고 한다.
이때 작업하는 두 차원은 그 크기가 같거나, 1이어야 한다고 한다.
When operating on two arrays, NumPy compares their shapes element-wise. It starts with the trailing (i.e. rightmost) dimension and works its way left. Two dimensions are compatible when
- they are equal, or
- one of them is 1.
[출처, numpy.org]
다음의 (3, 4, 4) shape를 가진 a배열이 있다고 치자.
가장 오른쪽 차원인 4부터 다른 b배열과 비교를 할 것이다.
b배열이 (4,)인 경우 부족한 차원은 1차원으로 간주되어 배열의 차원이 stretched 된다고 한다.
b배열은 (1, 1, 4)배열이 된다.
둘의 마지막 차원부터 비교를 하면, 4와 4가 같고, 4와 1은 둘 중 하나가 1이므로 괜찮고, 3과 1도 둘 중 하나가 1이므로 (3, 4, 4)와 (4,)는 broadcasting이 가능한 것이다.
broadcasting이 얼마나 효과가 좋은지 아래 코드로 테스트 해보았다.
import numpy as np
import time
# 큰 리스트와 NumPy 배열 생성
list_X = [[i for i in range(1000)] for j in range(1000)]
np_X = np.array(list_X)
# 리스트에서 모든 값을 2배로 곱하기
start = time.time()
list_result = [[x * 2 for x in row] for row in list_X]
end = time.time()
print(f"리스트 곱셈 시간: {end - start}초")
# NumPy에서 모든 값을 2배로 곱하기 (벡터화 연산)
start = time.time()
np_result = np_X * 2
end = time.time()
print(f"NumPy 곱셈 시간: {end - start}초")
"""
리스트 곱셈 시간: 0.06800007820129395초
NumPy 곱셈 시간: 0.0020034313201904297초
"""broadcasting을 사용한 NumPy배열 연산이 단순 python 리스트 연산보다 30배 이상 빠르다.
그러나 평범한 인덱싱 시에는 다음과 같이 python 리스트가 NumPy배열보다 좋은 성능을 보였다.
import numpy as np
import time
# 큰 리스트와 NumPy 배열 생성
list_X = [[i for i in range(1000)] for j in range(1000)]
np_X = np.array(list_X)
# 파이썬 리스트 인덱싱 시간 측정
start = time.time()
for i in range(1000):
for j in range(1000):
value = list_X[i][j]
end = time.time()
print(f"리스트 인덱싱 시간: {end - start}초")
# NumPy 배열 인덱싱 시간 측정
start = time.time()
for i in range(1000):
for j in range(1000):
value = np_X[i, j]
end = time.time()
print(f"NumPy 인덱싱 시간: {end - start}초")
"""
리스트 인덱싱 시간: 0.11900091171264648초
NumPy 인덱싱 시간: 0.19500255584716797초
1000 * 1000 배열에서의 차이 0.07600164413452149
2000 * 2000 배열에서의 차이 0.15662693977355956
3000 * 3000 배열에서의 차이 0.34084367752075195
"""NumPy배열이 단순 인덱싱에서는 파이썬 리스트보다 느린 것을 알 수 있다.
배열 크기에 정비례해서 차이가 일정하게 커지지도 않는다...
gpt에게 위 논문에서 근거를 찾아달라고 부탁했더니 다음과 같은 답변을 받았다.
Strides:
"Strides are necessary to interpret computer memory, which stores elements linearly, as multidimensional arrays."
이 문장은 NumPy가 다차원 배열을 처리하기 위해 메모리 내에서 데이터를 선형적으로 저장하고, 이를 해석하기 위해 strides(메모리 이동 양)을 필요로 한다고 설명합니다. 이는 다차원 배열의 인덱싱 시 추가적인 계산이 필요함을 나타냅니다.Indexing:
"Indexing an array returns single elements, subarrays or elements that satisfy a specific condition."
이 문장은 배열 인덱싱이 단일 요소, 서브배열 또는 특정 조건을 만족하는 요소를 반환한다고 설명하고 있습니다. 이는 NumPy의 인덱싱이 단순 리스트 인덱싱보다 더 복잡한 구조를 가지고 있음을 암시합니다.
대규모 연산을 효율적으로 하기 위한 처리들로 인해서 느려진다고 일단은 이해하고 넘어가려고 한다.
중요한 것은 연산이 빠르다는 것과 그 이유이니까.
결국 논문에서는 뭔가 중요한 자료는 못찾았고 NumPy 공식 문서를 읽어서 궁금증을 해결했다.
목적에 맞는 자료를 찾아서 공부하는 것도 중요하다는 것을 느꼈다. 이상
