AI, 딥러닝, 머신러닝 공부 일지

선형대수학에서 다중선형사상(multilinear map) 또는 텐서(tensor)는 선형 관계를 나타내는 다중선형대수학의 대상이다. [출처, 위키피디아] 위키피디아에 나와 있는 텐서의 정의 그만 알아보도록 하자. 농담이고, 작은 것부터 천천히 알아보자. 나는 저

이 글은 머신러닝 라이브러리 기초를 공부하면서 나의 생각의 흐름을 기록하기 위해 남겨둔 글이다.따라서 틀리거나 부족한 내용들이 있을 수 있다.이런 것들을 바로잡아나가는 과정 또한 이 시리즈의 주요 내용이다.위키피디아에서 먼저 정의를 찾아보았다.스칼라(수학) : 벡터 공

텐서 공부일지에서 벡터는 1차원 텐서라고 썼었다.이번에는 벡터에 대해 공부하며 생각한 내용들을 정리하는 글이다.강의에서 백터는 다음과 같은 특징을 갖고 있다고 말하고 있다.1차원 배열소문자이면서 두꺼운 이탤릭체로 표기함 e.g. x(스칼라는 소문자 이탤릭체로 표기했었음

2차원 배열로 표현이탤릭체 대문자, 두꺼운 글씨로 표기함 e.g. X2차원 텐서의 원소는 이탤릭에 대문자로 표기함 e.g. X1,2X = \[25, 2, 5, 26, 3, 7] 라는 2차원 배열은X = np.array(\[25, 2, 5, 26, 3, 7]) 이렇게 넘

행렬 텐서 공부중에 gpt가 다음과 같이 대답을 하는 것을 봤다.차이점 요약:리스트: X행처럼 두 번 접근.NumPy 배열: X행, 열처럼 한 번에 접근.파이썬 리스트와 NumPy로 만든 배열의 차이점을 물어봤을 때 내놓은 대답이었다.먼저 리스트(list)와 배열(ar

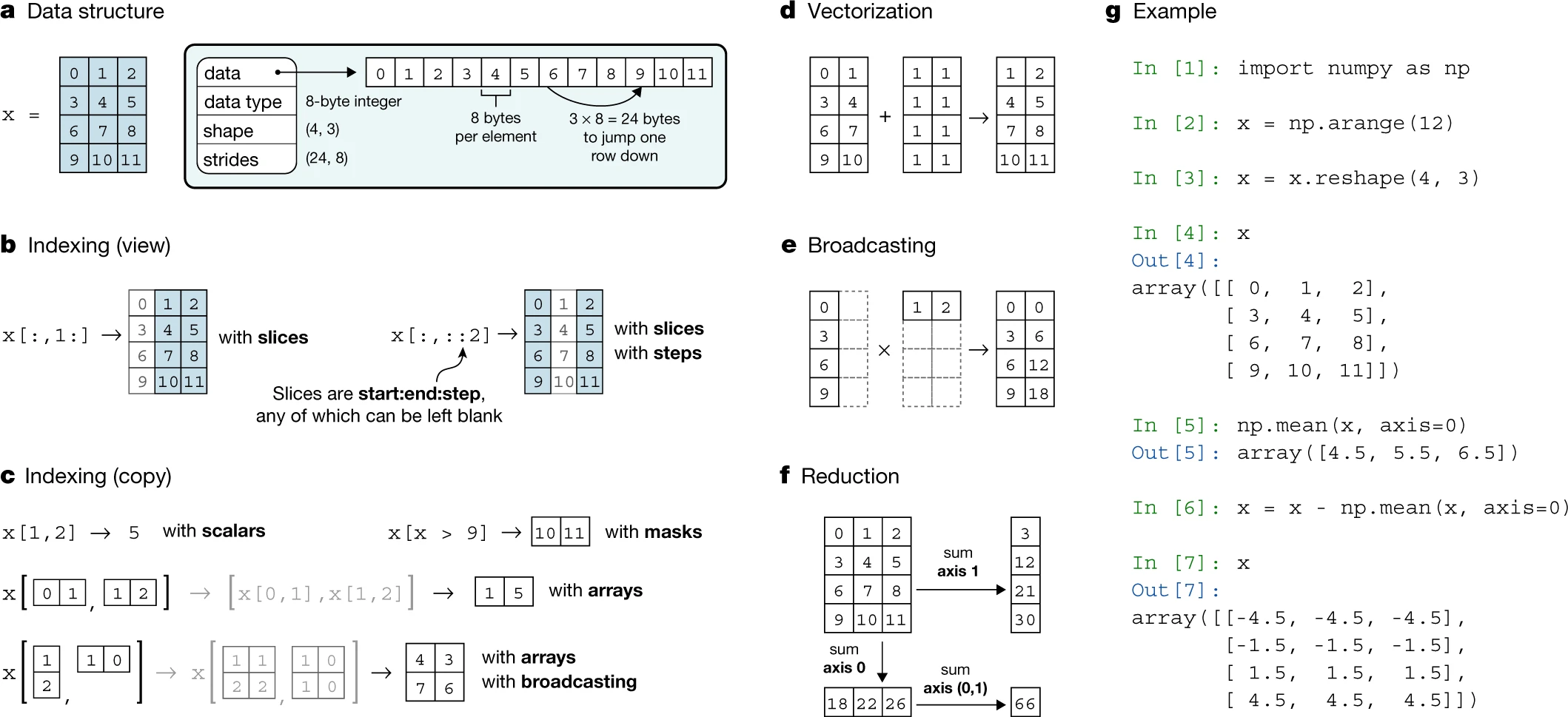
gpt에 NumPy 배열의 구조를 잘 알려주는 자료를 달라고 하니 다음 논문을 알려줬다. Harris, C. R., Millman, K. J., van der Walt, S. J., et al. (2020). Array programming with NumPy. Nat

기초적인 텐서 연산에 대해 공부했다.곱, 더하기, 아마다르 곱, 리덕션, 내적을 배웠으며실제 사용되는 텐서연산은 보다 다양한 종류가 있다고 한다.여기서 말하는 곱은 텐서끼리의 곱이 아닌, 텐서와 스칼라의 곱이다.스칼라는 텐서의 모양을 유지하면서 모든 요소에 더해지거나

분석을 용이하게 하거나 복잡성을 줄여 연산에 용이하게 만들 목적으로 다차원 텐서의 차원을 줄이는 것즉 어떤 방식이든 차원이 줄어들면 리덕션이라고 일단 이해했다.합(Sum)평균(Mean)최대(Max)최소(Min)위와 같은 방법들이 있으며, 이번 공부에서는 sum만 다루어

선형대수학에서 스칼라곱 또는 점곱(dot product)은 유클리드 공간의 두 벡터로부터 실수 스칼라를 얻는 연산이다스칼라곱이 유클리드 공간의 내적을 이루므로, 이를 단순히 '내적'이라고 부르기도 한다.\[출처, 위키백과]대수적 정의는 백터(1차원 텐서)의 같은 성분끼

이전에 배웠던 L2 norm(유클리드 norm)의 확장 개념이라고 한다.\[참조, 관련 공부일지]지금까지 배웠던 norm은 벡터(1차원 텐서)에서만 사용됐었지만, Frobenius norm은 다차원 배열(n차원 텐서)에서 사용한다.||X||F 로 표현한다.

ai 공부에 필요한 수학적 기초만 다지다가 슬슬 ai의 이론적인 부분 공부를 시작했다.이론적인 부분에 들어가기 전 AI와 머신러닝, 딥러닝이 어떻게 관련돼있는지전체적인 지도를 그려두고 내 위치를 확인해가며 공부할 예정이다gpt로 먼저 시작점을 잡고, 구글링을 하는 방법

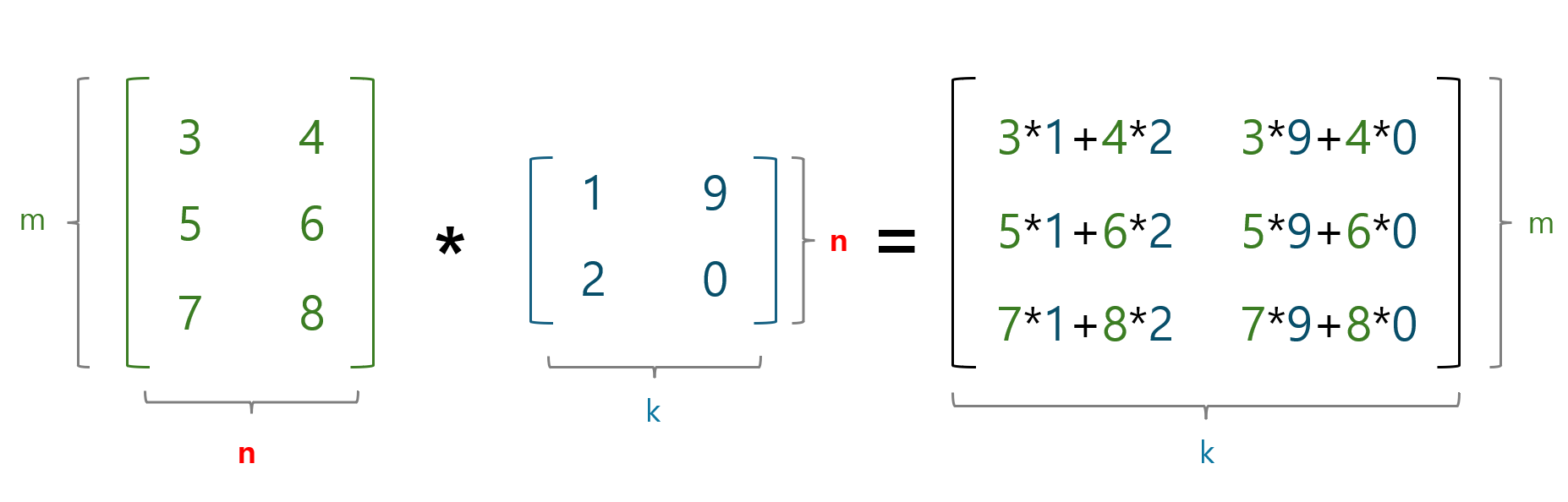
행렬 곱의 기본적인 내용과 사용되는 예시를 알아봤다.학부생 때 수학과목에서 배웠던 행렬의 기초적인 부분들을 슬슬 떠올려가며 공부했다..A행렬과 B행렬을 곱하여 C행렬을 만든다고 할 때,A행렬의 열과 B행렬의 행의 수가 같아야하며, 만들어진 C행렬의 행은 A행렬의 행과

강화학습 중 Q-Learning 부분을 공부했다.

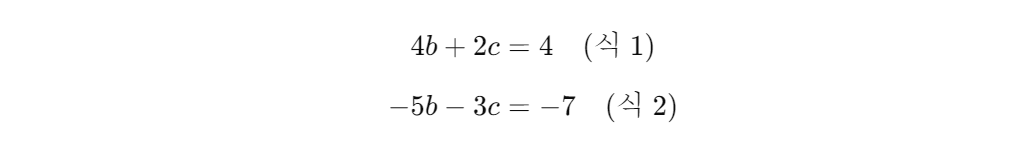
대칭 및 단위행렬 대칭 행렬은 주대각을 기준으로 대칭인 행렬이다. (n, n)모양이며(행개수 = 열개수) XT = X 이다. 단위행렬은 대칭행렬이면서 주대각 요소가 1인 행렬이다. 다른 요소는 전부 0이다. In로 표현한다. (n = 행 또는 열개수) 단위행렬에 n

들어가기 전, 에이전트가 행동 A를 선택하는 방법에 대해 먼저 알아보고 갔다.이전에 배웠던 벨만 방정식에서 나오는 그 A다.결정론적 탐색(Deterministic Search)에이전트가 같은 상태에서 100% 확정된 선택을 하는 방식이라고 한다.그러나 현실세계에서는 예

정책과 계획에 대해 배웠다.임의적인 요소를 다룰 때는 이전에 공부했던 결정론적 탐색을 사용할 수 없기 때문에'계획' 또한 세울 수 없다.계획은 다음 행동, 다음 단계를 정확히 알고 있을 때만 가능하기 때문이라고 한다.특정 상태에서 에이전트가 각 행동을 선택할 확률이 있

아fㅏ인 트랜스포메이션에 대한 학습 일지이다.영어로 affine transformation 이고 아파인 이라고 발음한다고 한다.오랜만에 정리를 하는 것이라 잡소리를 좀 해봤다. ㅎㅎ기하학에서 아핀 변환은 아핀 기하학적 성질들을 보존하는 두 아핀 공간 사이의 함수이다.\

강의에서는 행렬 변형 이후 벡터스팬을 잃지 않았으면 고유벡터라고 할 수 있다고 한다.쉽게 말하면 행렬 변형 이후에도 이전과 같은 선 상에 놓여 있으면 고유벡터인 것이다.\[이미지 출처, 위키피디아]위 그림에서 파란색 화살표는 방향이 변하지 않았고, 같은 선 상에 있으니

Matrix Determinant에 대해 배워봤다.수학적으로 너무 깊게 들어갔다가는 영영 머신러닝 못 배울 것 같아서일단 퀵하게 보고, 필요할 때마다 좀 더 딥다이브 하는 방법으로 공부할 계획이다.행렬식이라고도 하고, 강의에서는 행렬 판별식이라고 했는데, 후자가 좀 더

아래와 같은 지도에서 최적의 경로를 찾는 Q-Learning을 구현해보았다. Q-Learning 구현에 앞서서 gamma와 alpha값을 설정한다. gamma(γ)는 미래 보상에 대한 가중치이다.(할인계수) gamma가 1에 가까울수록 장기적인 보상을 크게 생각하고