대칭 및 단위행렬(Symmetric Matrix, Identity Matrix)
대칭 행렬은 주대각을 기준으로 대칭인 행렬이다.
(n, n)모양이며(행개수 = 열개수)
XT = X 이다.
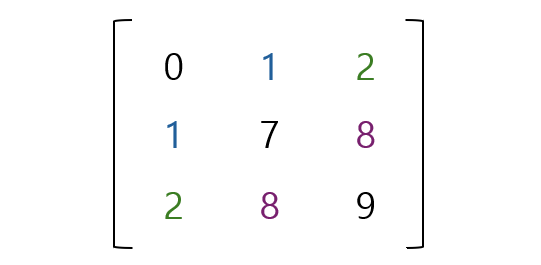
단위행렬은 대칭행렬이면서 주대각 요소가 1인 행렬이다.
다른 요소는 전부 0이다.
In로 표현한다. (n = 행 또는 열개수)
단위행렬에 n개수를 맞춰서 벡터나 행렬을 곱하면 곱하기 전 값이 그대로 나온다(항등원)
역행렬(Inverse Matrix)
선형방정식을 컴퓨터로 풀어낼 수 있는 편리한 연산법
소거법이나 치환법으로 풀어내는 것보다 훨씬 편리하다고 함
행렬 X의 역행렬은 X -1로 나타낸다.
X -1 X = In 을 만족한다.
행렬곱을 사용해서 신경망의 곱을 계산했던 예시에서
y = Xw 를 만족한다고 배웠었다.
여기서 X -1가 존재한다고 가정하면 w를 구할 수 있다.
Xw = y
X -1Xw = X -1y
Inw = X -1y
w = X -1y
아래와 같은 선형방정식에서 역행렬을 사용하여 w를 구할 수 있다.
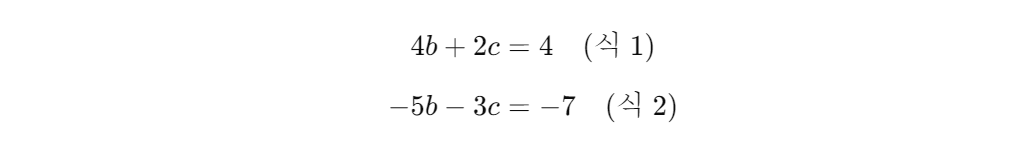
위 방정식의 요소들을 행렬로 나타내면 아래와 같다.
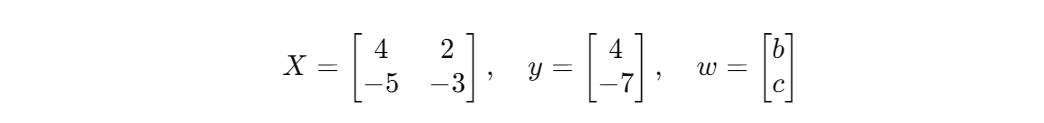
Xw = y 모양으로 만들어준다.
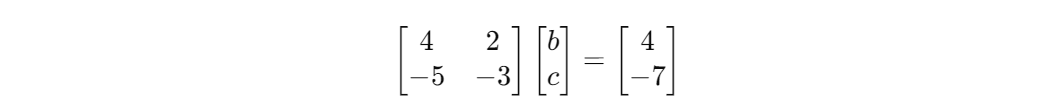
계산하면 b = -1, c = 4라는 결과물이 나온다.
그러나 역행렬을 구하는 데 O(n3)의 시간이 소요되고,
행렬이 특이행렬일 경우XTX 가 비가역적이어지기 때문에 역행렬을 구할 수 없어서
머신러닝에서 대규모 데이터 셋에는 잘 사용하지 않는다고 한다.
*추가로 행렬이 정방행렬(정사각형)인 경우에도 과결정되거나 불충분결정된 경우가 생겨 역행렬을 사용할 수 없다고 한다.
* 특이 행렬의 XTX 가 비가역적인 이유는 행렬 X의 열 벡터들이 선형 독립하지 않기 때문이다.
이 말은 선형 방정식들을 그래프로 그렸을 때 완전히 겹치거나(해가 무한함),
평행한 경우(해가 없음)를 말한다.
역행렬은 주로 이론적 배경이나 소규모 문제에서 사용한다고 한다.
대각행렬(Diagonal Matrix)
대각행렬은 주대각성분을 제외한 나머지 요소가 모두 0인 행렬
꼭 정방행렬이 아닌 경우도 있으며, 연산효율적이다.
개념의 크기대로 나열하면 대칭행렬 > 대각행렬 > 단위행렬이다.
직교행렬(Orthogonal Matrix)
이전에 다뤘던 기저벡터, 직교벡터 내용을 참고하면 좋다.
직교행렬Q는 다음과 같은 특징을 갖고 있다.
- QTQ = I를 만족한다.
- 직교행렬의 각 행과 열은 서로 직교하며, 길이(norm)가 1인 정규직교벡터로 이루어져 있다.
두번째 특성때문에 QTQ = QQT = I 가 성립한다.
위 식은 곧 QT = Q -1I = Q -1을 의미한다.
QT 연산은 효율적이지만, Q -1연산은 아주 비효율적이기 때문에 위 식은 유용하게 쓰인다.
