1. Vector intro for linear algebra

Vector has both magnitude and direction.

• Speed is not a vector. This is considered to be a scalar quantity. If we want it to be a vector, we would also have to specify the direction.

• Velocity is a vector because it has magnitude and direction.

And the interesting thing is that we only care about magnitude & dirrection. We don't necessarily not care where we start and where we place.

2. Real coordinate spaces

When you see R2 in your textbook, it means that 2-dimensional real coordinate space.

• 2 tells how many dimensions are there.
• R tells Real Cartesian coordinate space. This space is all the possible real-valued 2-tuples.
• tuple means an ordered list of numbers. neither numbers have imaginary numbers.

3. Adding vectors

They are the some regardless of Addition order

4. Multiplying a vector by a scalar

1. If you multiply -1, then the direnction of vector will be exactly opposite!
2. If you multiply possitive number scalar except 1, then the magnitude of vector will be changed!

• ex. multiplying with a negative scalar
  a = [2,1]
  -1a = [-2, -1]
  

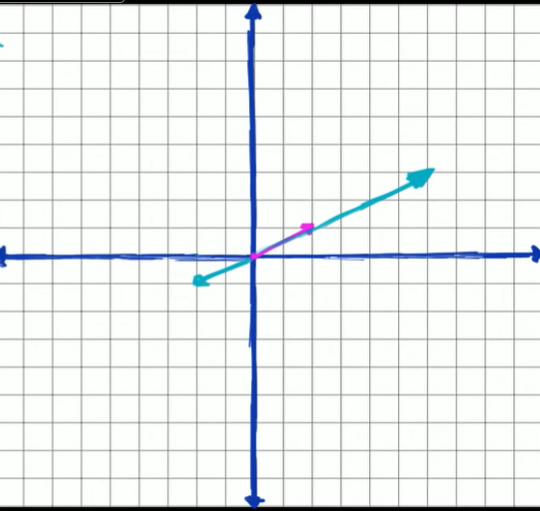
5. Vector examples

Standard position is just to start the vectors at 0, 0 and then draw them.
You can start vector at any point in R2

• Subtraction
  ex. x = [2,3], y = [-4, -2]
  x - y = x + (-1 * y) = [6, 5]
  y - x = [-6 ,-5]

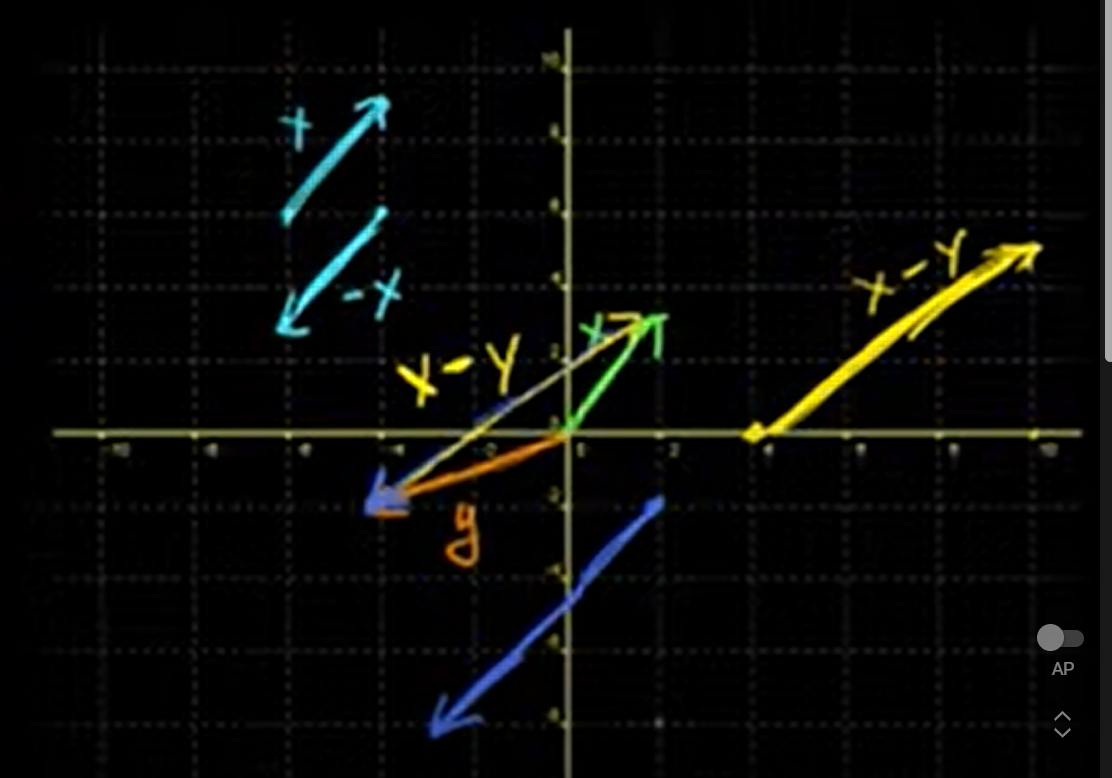
• Generalization (not only in 2-D space)
  ex. In R4
  a = [0, -1, 2, 3] , b = [4, -2, 0, 5]
  4a - 2b = [-8, 0, 8, 2]

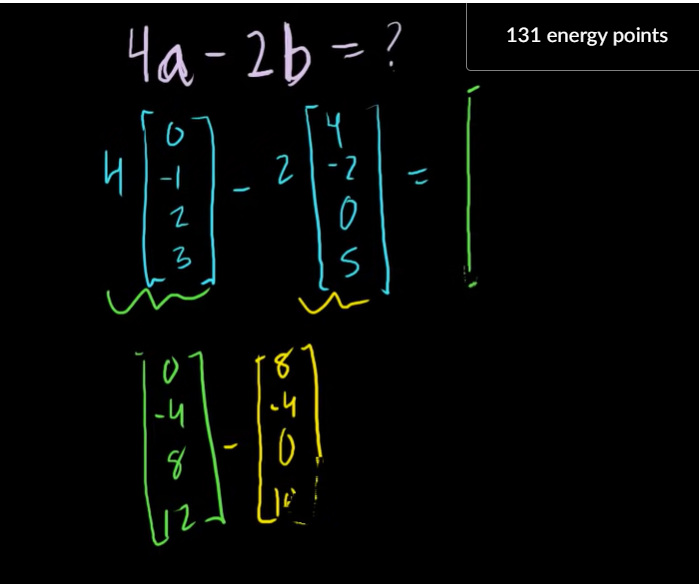
6. Unit vectors intro

Unit vector is a vector which has length 1.

Any 2-dimensional vectors can be represented with two vectors(i=[1,0], j=[0,1])

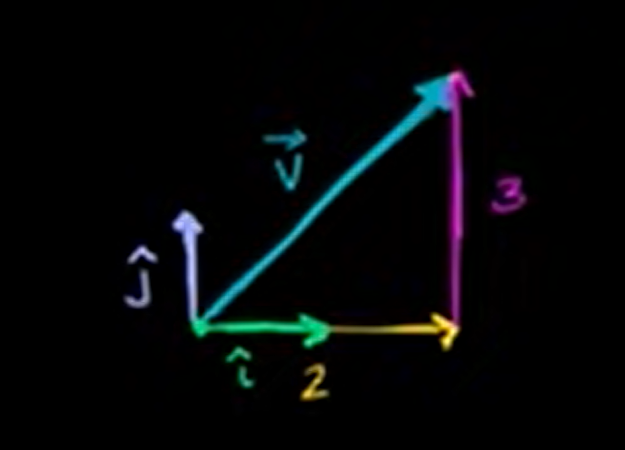
v = 2i + 3j

7. Parametric representations of lines

Let's define some vectors.

Ex1

$\vec {v}= \left[\begin{matrix}2\\1\\ \end{matrix}\right]$
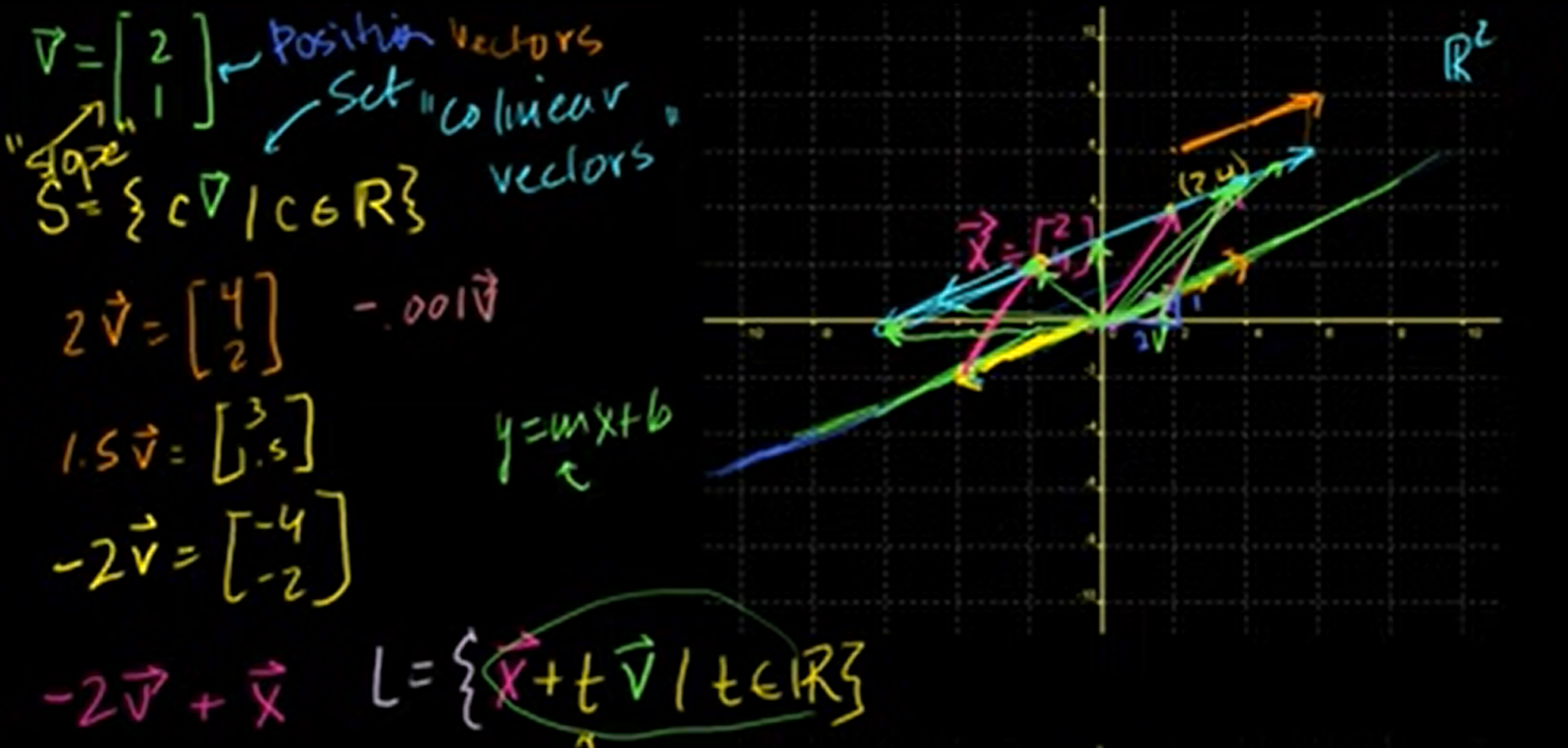
$\vec {v}$ starts at the origin because $\vec {v}$ is a position vector.

S = $\{ c\cdot \vec{v} |c\in \mathbb{R}\}$

What if we want to represent a parallel line that goes through that point over (2,4)?

$\vec {x} = \left[\begin{matrix}2\\4\\ \end{matrix}\right]$

And let's define another set.
L = $\{ \vec {x} + t\vec{v} |t\in \mathbb{R}\}$

• t is parametrization of the line

Why should we use L instead of y=mx+b equation?
y=mx+b can only work well in R2. But line L can work at any dimension. That's why we represent a line like that.

Ex2

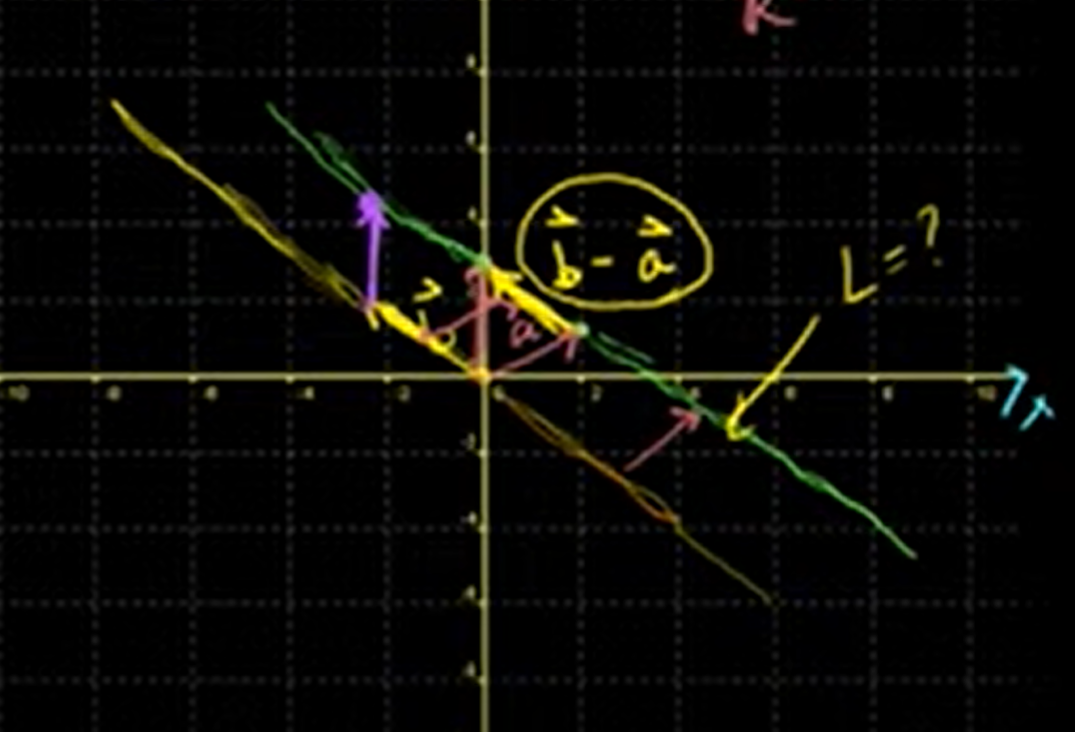
$\vec {a} = \left[\begin{matrix}2\\1\\ \end{matrix}\right]$ , $\vec {b} = \left[\begin{matrix}0\\3\\ \end{matrix}\right]$

L = $\{ \vec {b} + t(\vec{b} - \vec{a})|t\in \mathbb{R}\}$

We can also represent like this way.
Li = [L1, L2] = $\left[\begin{matrix}0-2t\\ 3+2t\\ \end{matrix}\right]$

• L1: x-coordinate
• L2: y-coordinate

It's really easy in 2-Dimensional space, but how do you present lines in three dimensions?

Ex3

$\vec {P_1} = \left[\begin{matrix}-1\\2\\7\end{matrix}\right]$ , $\vec {P_2} = \left[\begin{matrix}0\\3\\4\end{matrix}\right]$

These vectors are in R3.

L = $\{ \vec {P_1} + t(\vec{P_1} - \vec {P_2})|t\in \mathbb{R}\}$

• x-coordinate = -1 + (-1)t
• y-coordinate = 2 + (-1)t
• z-coordinate = 7 + 3t

Then our line can be described as a set of vectors.

As we are dealing in R3, the only way to define a line is to have a parametric equation.

x+y+z = k is not a line!! This is a plane. The only way to define a line or a curve in three dimensions, it has to be a parametric equation!.