02. Linear combinations and span

Linear combination: an expression constructed from a set of terms by multiplying each term by a constant and adding the results.

Let's see some examples of linear combination.

There are two vector which is

$\vec {a} = \left[\begin{matrix} 1\\ 2 \end{matrix}\right]$ , $\vec {b} = \left[\begin{matrix}0\\3\end{matrix}\right]$

When we scale by some scaling factor and add them, we can get those vectors and it's called a linear combination.

ex1) $0 \cdot \vec {a} + 0 \cdot \vec {b} = \left[\begin{matrix} 0 \\ 0 \end{matrix}\right]$

✔ zero vector is also a linear combination!

ex2) $3 \cdot \vec {a} + (-2) \cdot \vec {b} = \left[\begin{matrix} 3 \\ 0 \end{matrix}\right]$

Then what is the set of all of the vectors we could have created by taking linear combinations?

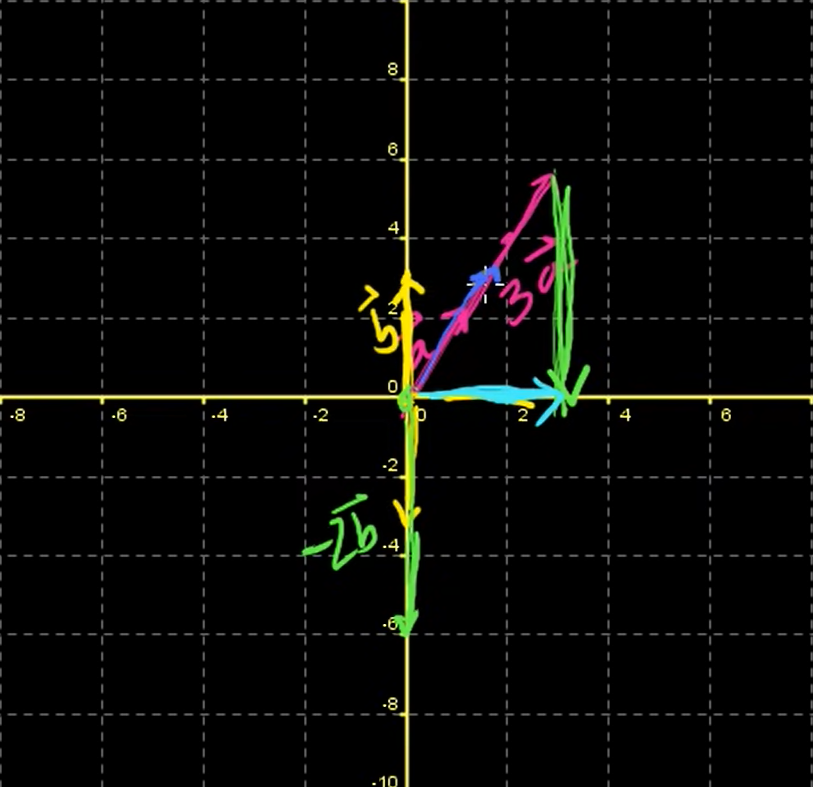
You can represent any vectors with some linear combinations of these vectors in R 2.

span( $\vec {a}, \vec {b}$ )

span $( \vec {0} )= \left[\begin{matrix} 0\\0\end{matrix}\right]$

span$(\vec {v_1},\vec {v_2}, \ldots,\vec {v_n})$ = {${{c_1}\vec {v_1},{c_2}\vec {v_2}, \ldots,\vec {c_n}{v_n}} |{c_i} \space \in \mathbb{R} \space for \space 1\leq i \leq n$}

✔ span is the space of all of vectors that can be represented by a combination of these vectors.

✔ Any Dimension space can be represented by each unit vectors.

Conclusion

In this time, we learned that what do linear combination and span mean.