
Lecture 3
continues our discussion of linear classifiers. We introduce the idea of a loss function to quantify our unhappiness with a model’s predictions, and discuss two commonly used loss functions for image classification: the multiclass SVM loss and the multinomial logistic regression loss. We introduce the idea of regularization as a mechanism to fight overfitting, with weight decay as a concrete example. We introduce the idea of optimization and the stochastic gradient descent algorithm. We also briefly discuss the use of feature representations in computer vision.
Keywords: Image classification, linear classifiers, SVM loss, regularization, multinomial logistic regression, optimization, stochastic gradient descent
Slides:
http://cs231n.stanford.edu/slides/2017/cs231n_2017_lecture3.pdf
Recall from last time in lecture 02
We were talking about Challnges of recognition. We talked about the idea of image classification, talked about why it's hard, there's this semantic gap between the giant nubmer of grid that computer sees and the actual image that human sees.
And also we talked about the K-neareast neighbor classifier as kind of simple introduction.
And we talked about the Linear classification as the first sort of building block as we move toword neural networks.

multiclass SVM loss & logistic regression loss
loss function
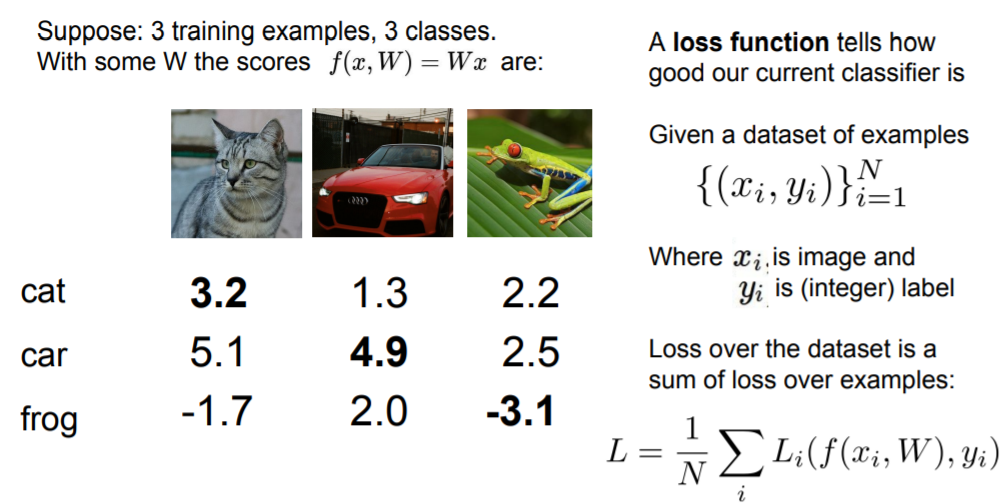

This type of function where we take max of zero and some other quantity is often referred to as some type of a hinge loss, and the name comes from the shape of the graph when we plot it.
S is predicted score for the classes that are coming oout of the classifier.
Syi corresponds to the score of the true class for the i-th example in the training set.
x_axis corresponds to the Syi that is the score of the true clas for some training.
y_axis is the loss. and you can see that as the score for the true category increases, then the loss will go down linearly until we get to above this safety margin and after that the loss will be 0. because we've already correctly classified this example.
SVM loss


For example, if we see the car case, the true class is car, so we're going to iterate over all the other categories. car scroe is much greather than those score of cat, frog. so we get no loss here.

But, if you go look at frog, you can see that frog score is very low, which incurs a lot of loss. so the loss for this class will be 12.9.
And the final loss over full dataset is the average of these losses across different examples.
The whole point of loss function is kind of quantify how bad are different mistakes.
Reguralization
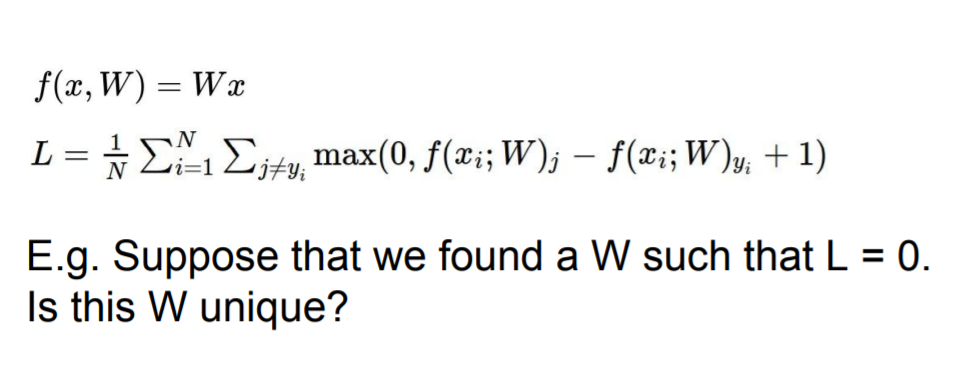
NO! the other Ws are which has L=0!
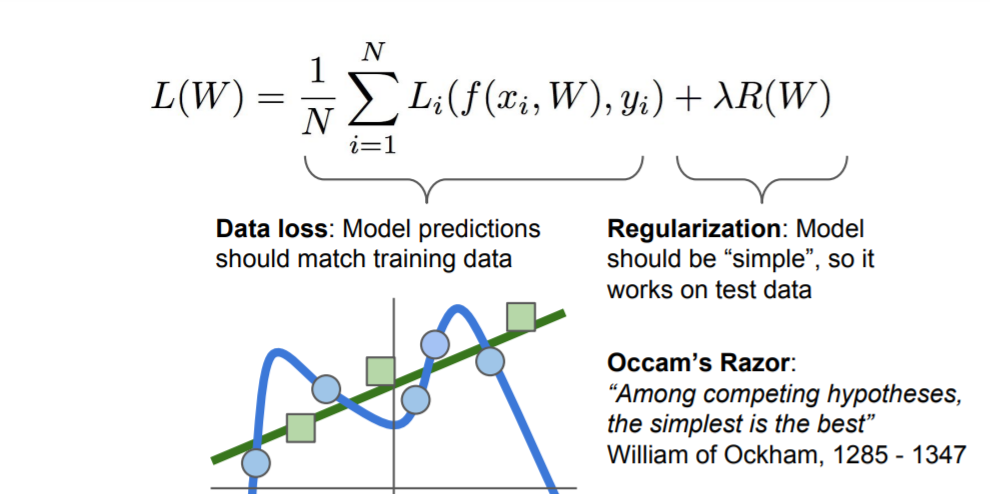
So, there are two terms which are Data loss and Regularization. What we really care is fitting well in test data(not on train data). And the hyper-parameter lamba trades off between the two.

L2 regularization is just the euclidean norm of weight vector W.
L1 regularization uses norm1. and this has some nice properties like encouraging sparsity in the matrix W.
Softmax Classifier
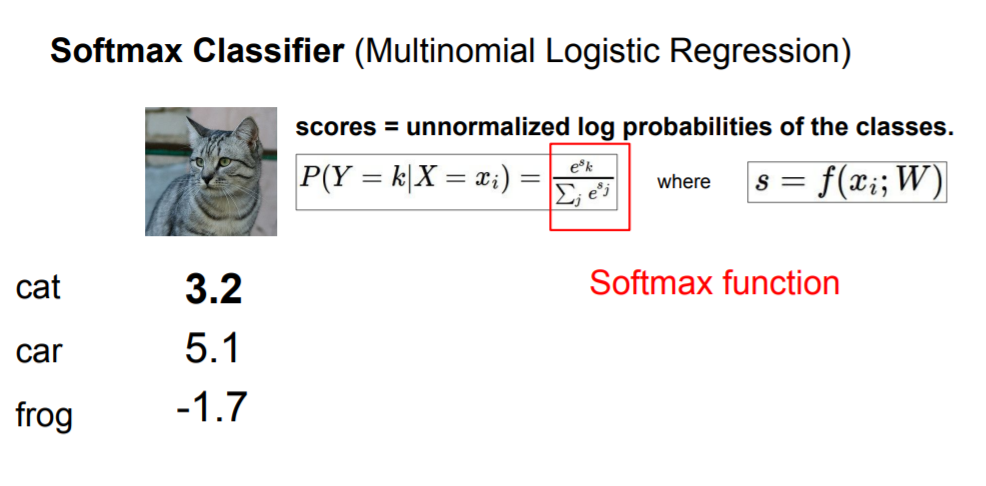
But, we didn't actaully have an interpretataion for those scores. We just said that we want the true score, the score of correct class to be greater than the incorrect classes, and beyond that we don't really say what those scores mean.
So, we will use those scores to compute a probability distribution over our classes. we call it softmax classifiers where we take all of our scores, and exponentiate them so that now they become positive. Then we normalize them by the sum of those exponents.
Now we have probabilites over our classes.

And we want to compare this with the target or true probability distribution. What we really want is that the probability of the true class is high and as close to one. So then our loss will be negative log of the probability of the true class.
Softmax vs SVM

Let's say if car score has much better than other incorrect classes.
Then the jiggling the scores for that car image won't change the multi-class SVM loss at all. Because the only thing that SVM loss cares about i s getting that correct score to be greater than a margin above the incorrect scores.
But the softmax loss is actually quite different in this respect. The softmax loss actually wants to drive that probability mass all the way to one. So, even if you get very high score to the correct class, and very low score to the incorrect to the all incorrect classes, softmax will want you to pile more and more probability mass on that correct class. Softmax will try to continuously improve every single data point to get better and better.
Recap
Optimization
But the question is that How do we acutally find this W that minimizes the loss?
That question leads us to the topic of optimization.

Random Search

The stupidest think is Random search. This is really bad algorithm,
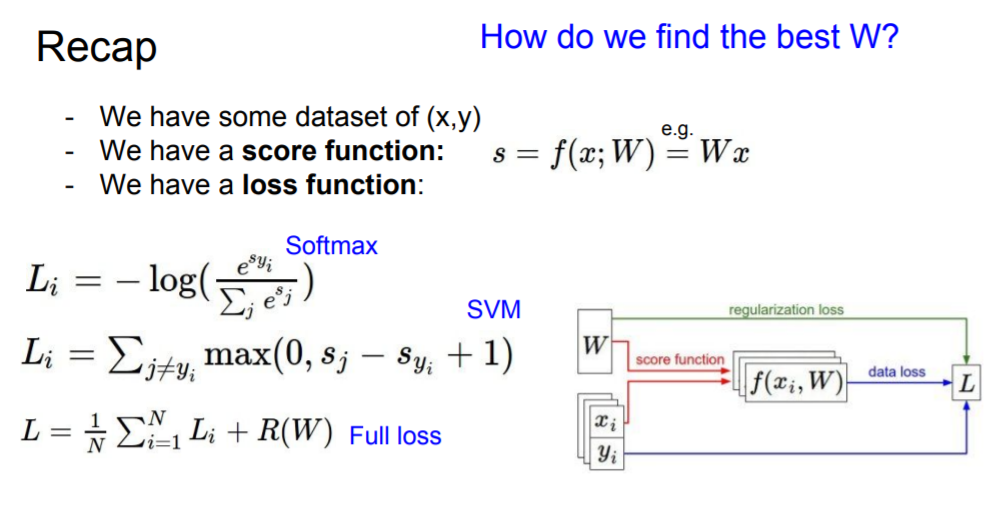
Follow the slope(local geometry)
Numerical Gradient


Analyitic Grdient


Gradient Descent

First it will initialize our W, then while True, computer will compute the thing and will update our wights in the opposite ofgradient direction.
step size is probably one of the single most important hyper-parameter you need to set.

We'll see more details about more at course.
SGD

Rememeber that we defined our loss function and our full loss over the data set was going to be the average loss across the entire training set.
But in practice, this N could be very large. so computing loss with this way could be very expensive. So we have to wait very long time before we make any individual update to W.
Rather than computing the loss and gradient over the entiring training set, instead at every iteration, we sample some small set of training examples, called minibatch. This is stochastic.
web demo
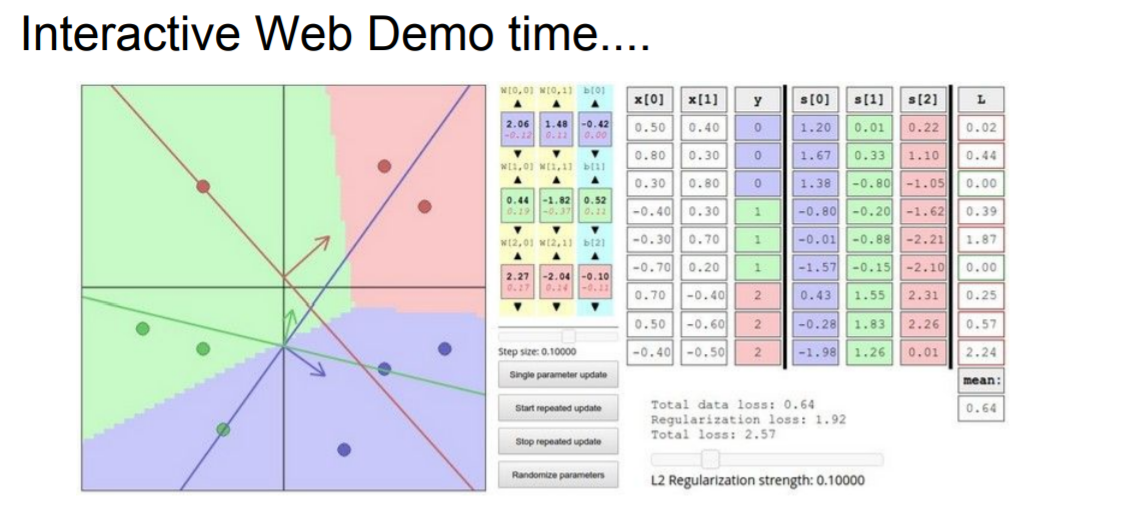
http://vision.stanford.edu/teaching/cs231n-demos/linear-classify/
recommend try to get some intuition for what it actually looks like to try to train these linear classifiers via gradient descent.
