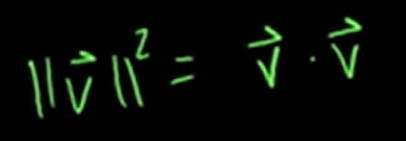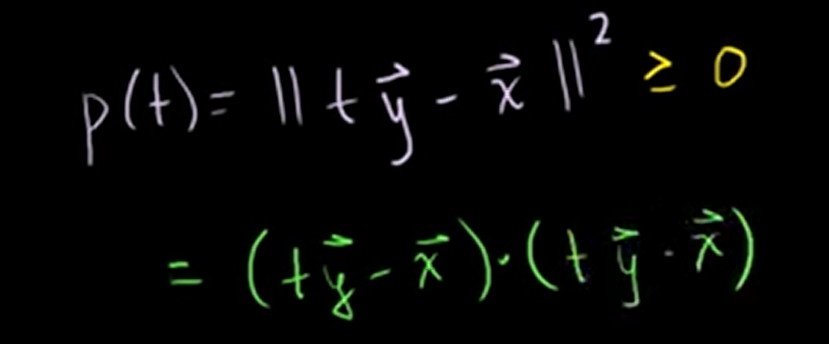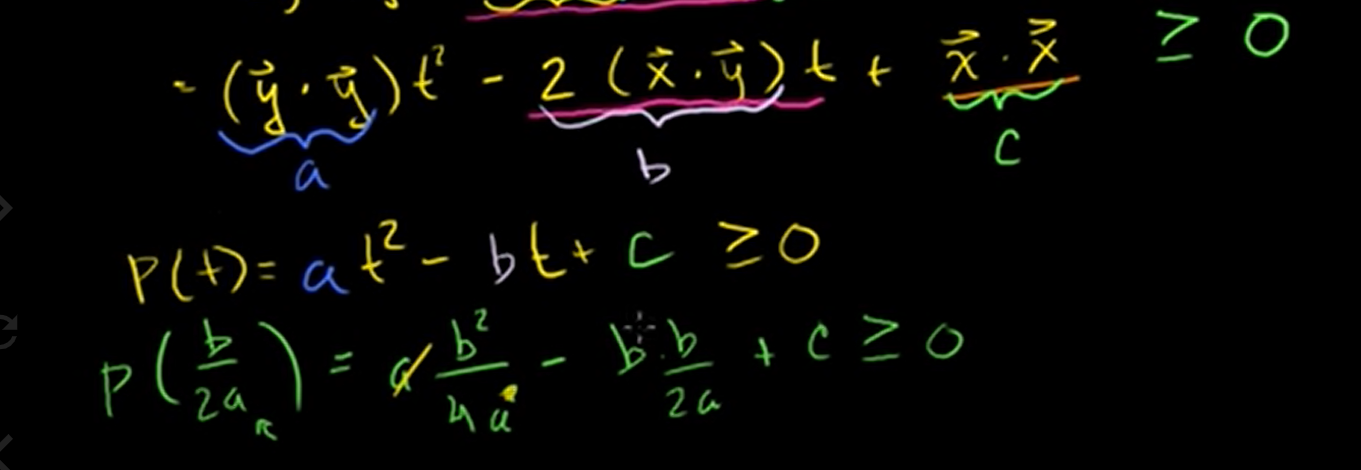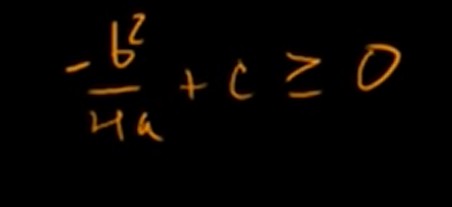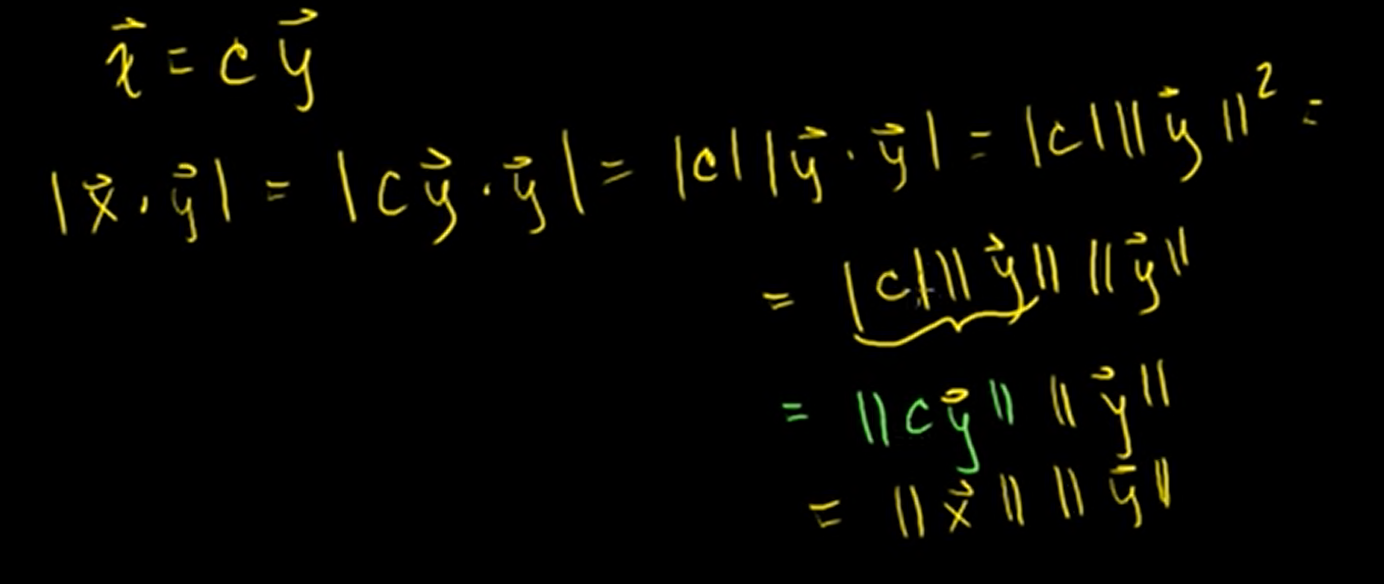Vector dot product and vector length

---

link

For multiplying vectors or taking the product, there's actually two ways. One of is the dot product.

You signfy the dot product by saying a dot b. They borrowed one of the types of multiplication.

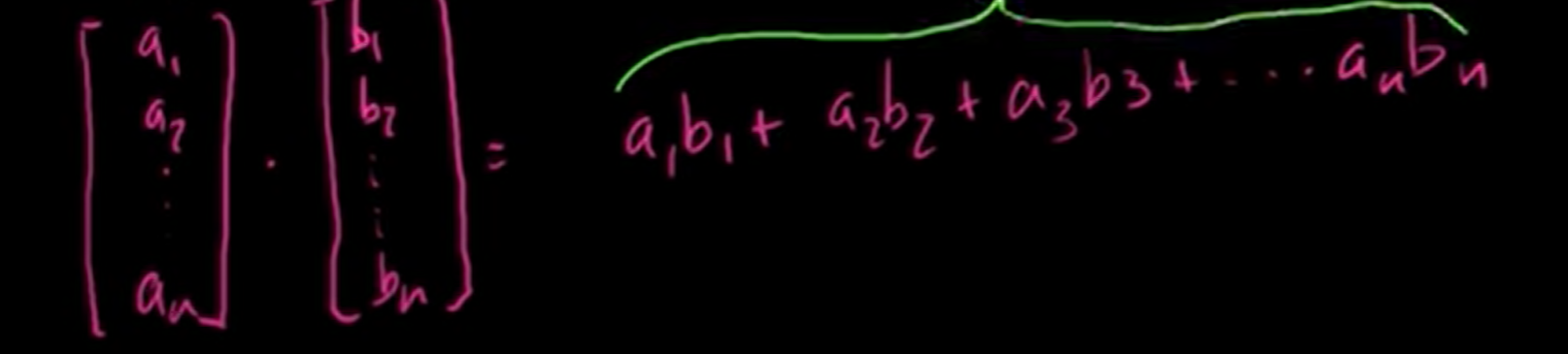
This is not a vector, this will be a real scalar. So the dot product, you multiply two vectors and you end up with a scalar value.

And let's define the length of a vector. Let's consider length in a colledge level. Because we're abstracting things to well beyond just $R^3$ or just three-dimensional space what you're used to.

So the definition about length is that the square root of each of the terms, each of my components, squared.

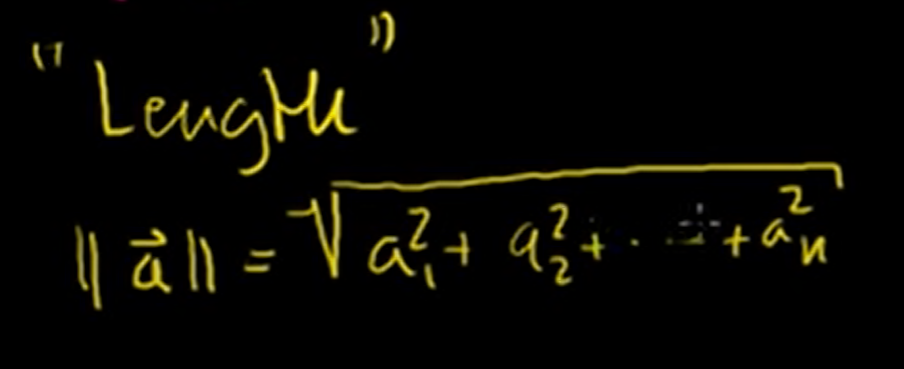
We can apply this notion of length at any dimension and start abstract beyond what we traditionally associate length with.

📖 Then, can we somehow relate length with the dot product?

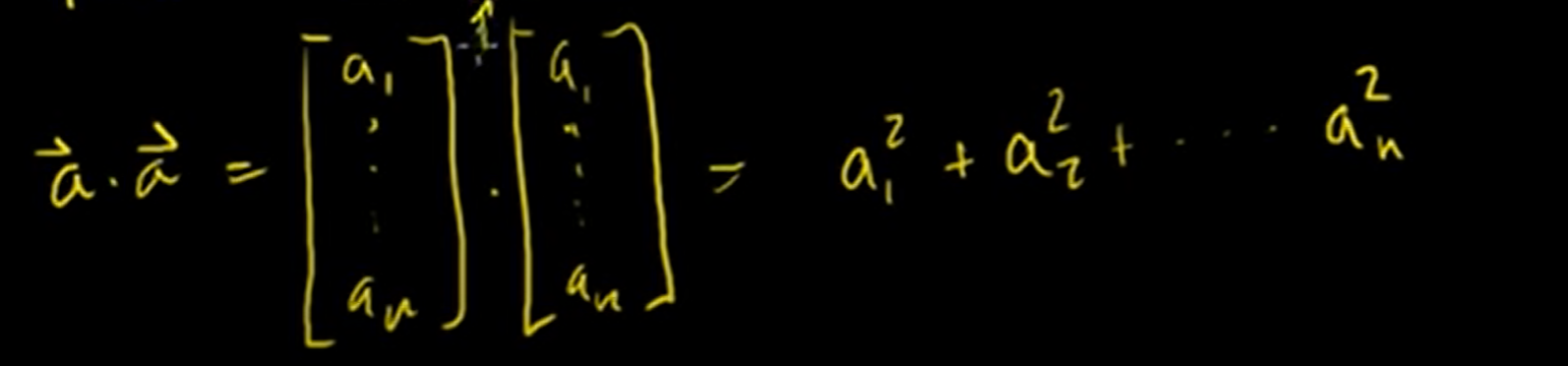
These two pictures are equivalent. So we could write our definition of vector length, we can write it in terms of the dot product, of our dot product definition.

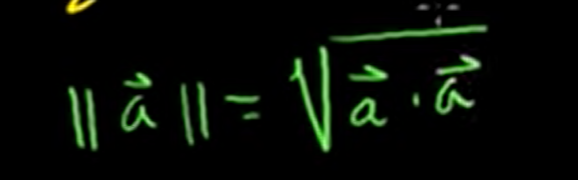
It equals the square root of the vector dotted with itself.

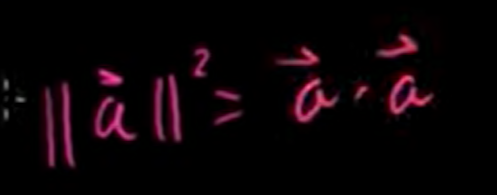
Or, if we square both sides, we could say that our new length definition squared is equal to the dot product of a vector with itself.

Proving vector dot product properties

---

link

1. Commutative property

That the order that I take the dot product doesn't matter.

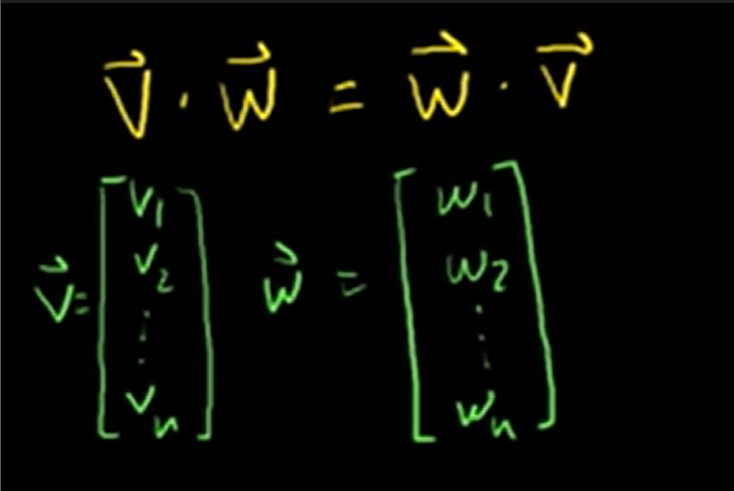
Let's prove this equation.

$\vec {v} \cdot \vec {w}$ = $\vec {w} \cdot \vec {v}$

We can say that $v_1 w_1 = w_1 v_1$ because we are dealing with regular numbers. And this is just a commutative property.

2. Distributive property

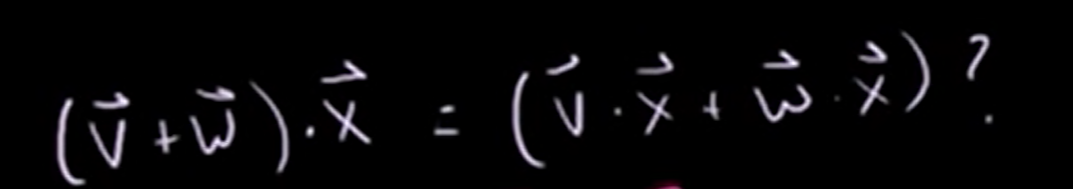
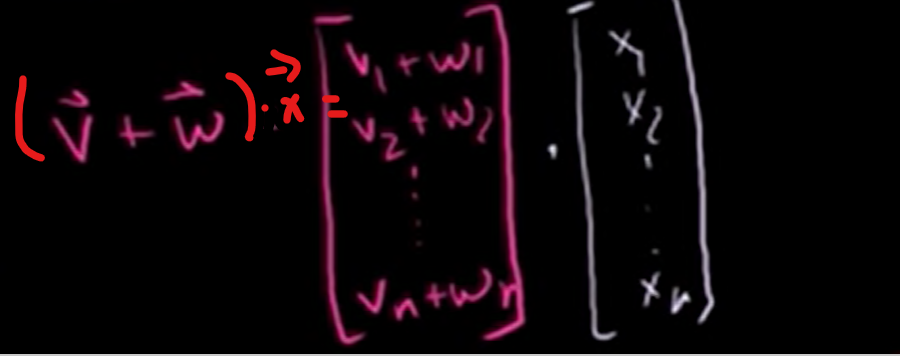
Let's see an example.

The result of left equation is like this below.

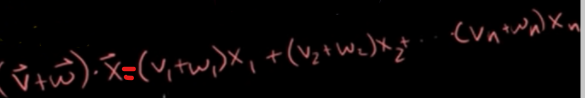
Let's see right side of the equation.

And we could factor the x out,

We just showed that they are the same!

3. Associative Property

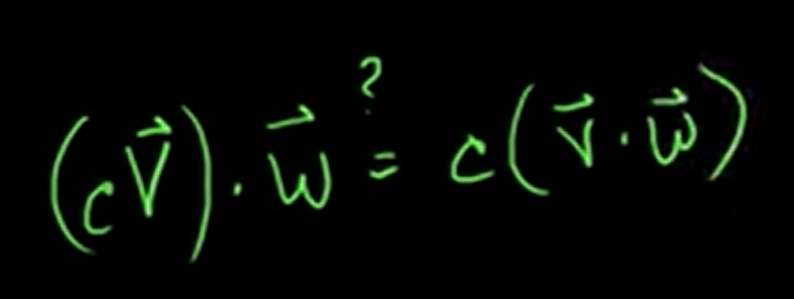
Let's see left side of the equation.

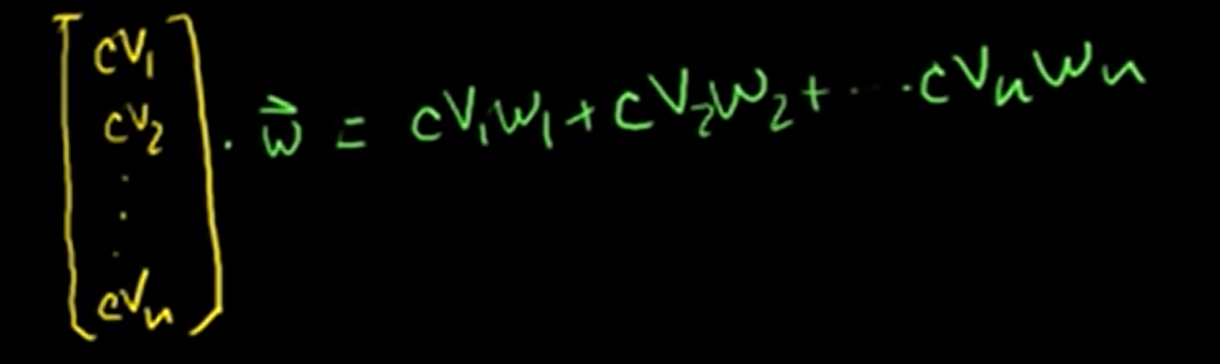
This is right side of the equation.

Proof of the Cauchy-Schwarz inequality

---

Let's say we have two vectors $\vec {x}, \vec {y} \space in \space \mathbb R^n$.

Then absolute value of x dot y is less than or equal to the product of their lengths. We call this inequation Cauchy-Schwarz inequality.

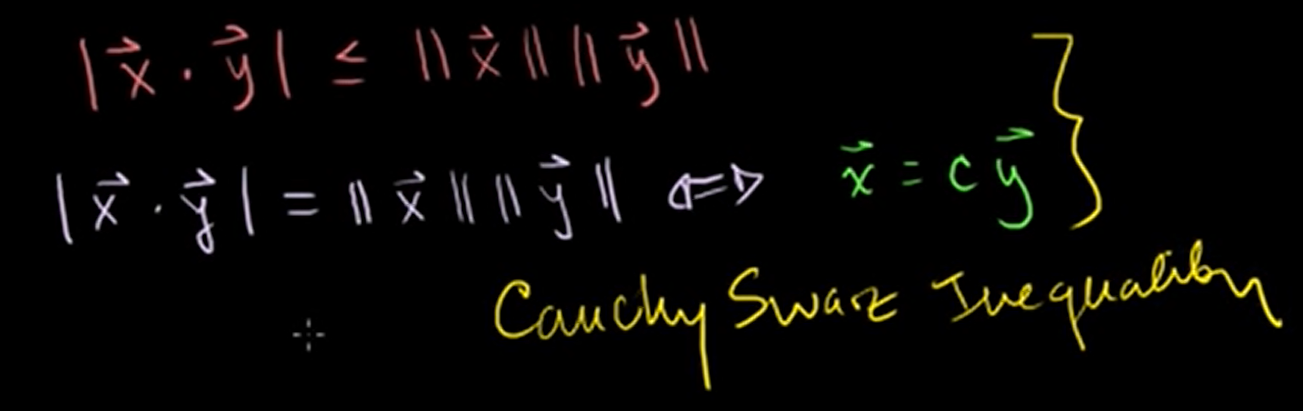
Let's make an function about variable t.

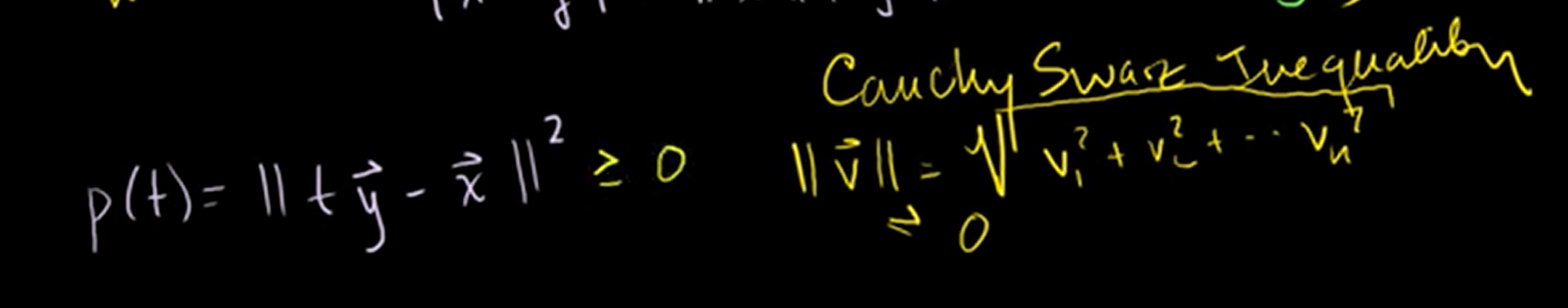
In last time, we knew that the magnitude or the length of a vector squared can also be rewritten as the dot product of that vector with itself.

• 

• 

After distribution, we can get this equation.

And let's define a, b, and c.

• 

• 

• 

• 

Let's substitute a,b,c with original vectors and take the square root of both sides.

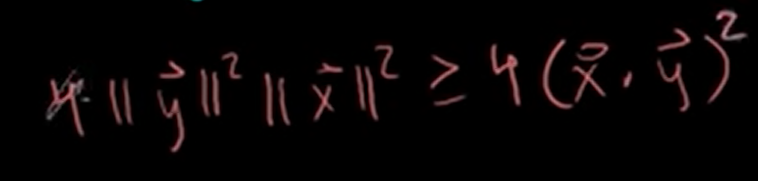
We got Cauchy-Schwarz inequality!

❔ What happens if $\vec {x} = c * \vec {y}$ ?

❕ Using associative property, we can get this equation!

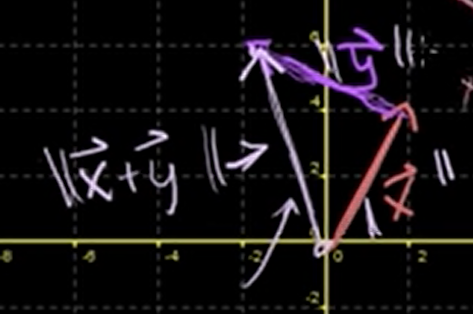
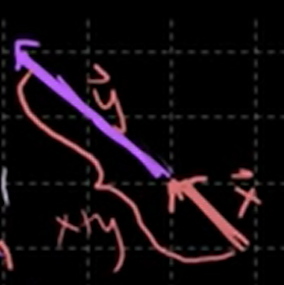
Vector triangle inequality

---

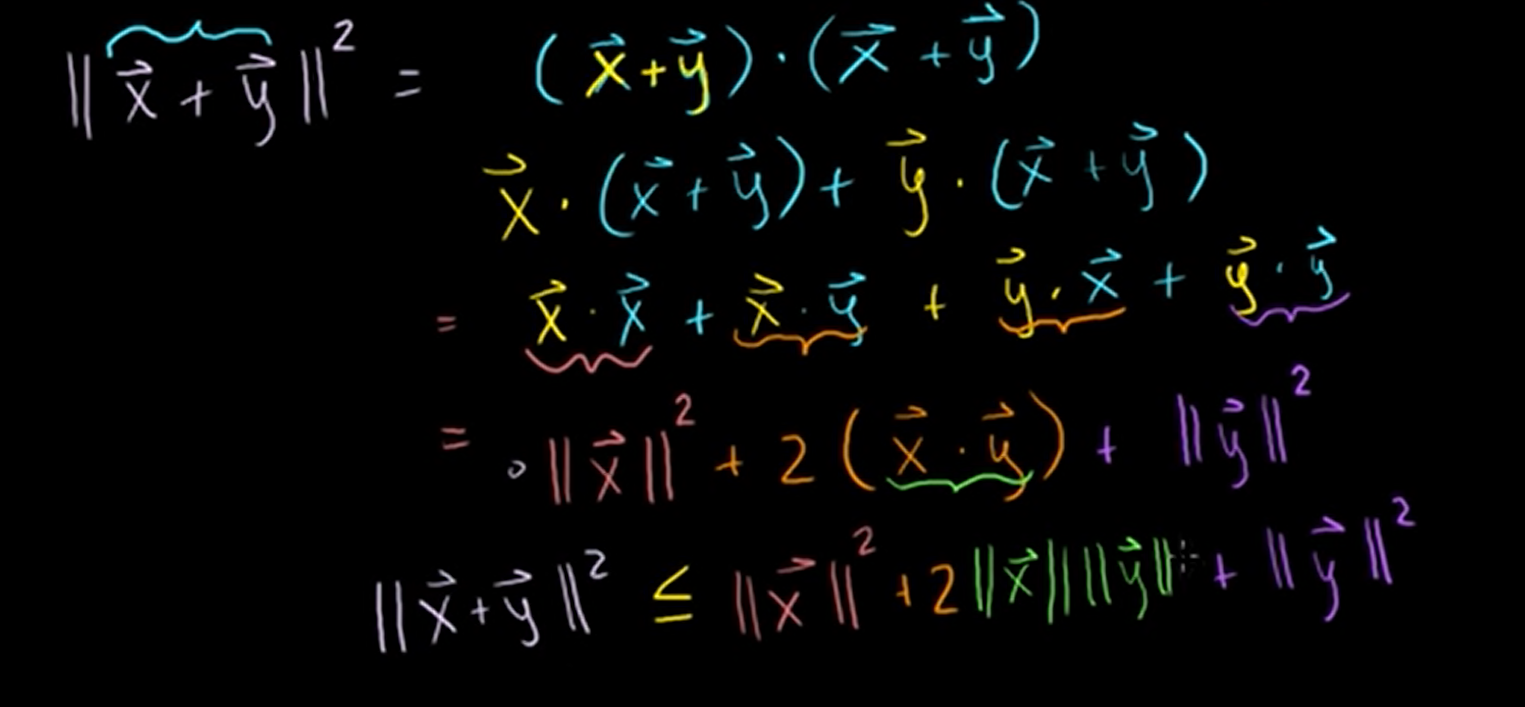
We call this "triangle inequality".

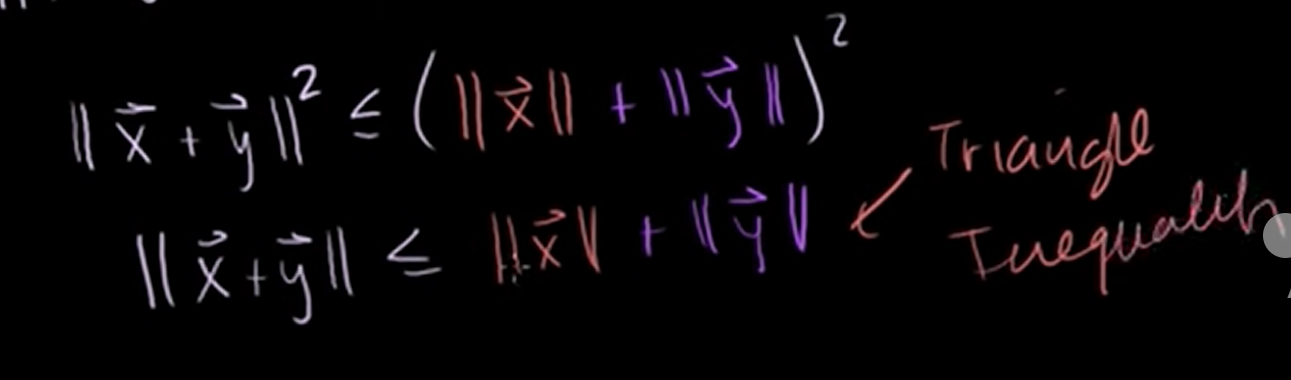
❔ Why is it called triangle inequality?

❕ Let's draw them

• 
• 

Defining the angle between vectors

Now let's define the angle between two vectors.

• Law of cosine

Defining a plane in R3 with a point and normal vector

Equation of a plane in $R^3$.

cross product introduction

• Dot product is defined in $R^n$
• Cross product is only defined in $R^3$

Proof: Relationship between cross product and sin of angle

Let's prove this equation.

And, we can get this equation.

Let's square this equation.

is equal to

---

Dot and cross product comparison/intuition

Until now, we've learned that $\vec {a} \cdot \vec {b}$ = $||\vec {a}|| \cdot ||\vec {b} || cos \theta$.

Normal vector from plane equation

Let's look about what the normal vector to a plane is.

Let's say we have some point ($x_p, y_p, z_p$), ($x, y, z$).

We ccan take the dot product between $\vec {P} - \vec {P_1}$ and $\vec {n}$. And they have to be equal to zero because this lies on the plane. This is perpendicular to everything!

If you have a normal vector and if you're given a point on the plane, we now have a very quick way of figuring out the equation.

But what about this?

How can we figure the normal vector out quickly?

Actually (Ax+By+Cz) part is completely analogous to the part (ax+by+cz).

The normal vector to this plane we started off with, it has the component a, b, and c.

The normal vector is going to be like this.

You can ignore D part because it won't fundamentally change how the plane is tilted.

Point distance to plane

When we want to find the minimum distance to a plane, we have to figure the perpendicular distance.

So the first thing we can do is just construct a vector between this point that's off the plane and some point that's on the plane. Let's construct a vector.

Orange vector $\vec {f}$ can be represented like this.

And we can tell that the shortest way to get to the plane is the yellow line. How can we figure out this length here?

We could say that cosine of theta is equal to the adjacent side over the hypotenuse.

But how do we figure out what theta is?

Let's multiply both side of equation with the magnitude of normal vector n and divide by n.

Then the numerator means the dot product of normal vector and vector f. So it's equal to the product of their magnitudes times the cosine of the angle between them.

Now let's calculate them.

We also saw this equation at last lecture.

This is all about the distance!!

For example, we have a plane (1x -2y +3z = 5) and a point (2, 3, 1) which is not in the plane.

Then we get the value $\frac{-6}{\sqrt{14}}$.

Distance between planes

To calculate the distance, the planes should be parallel.

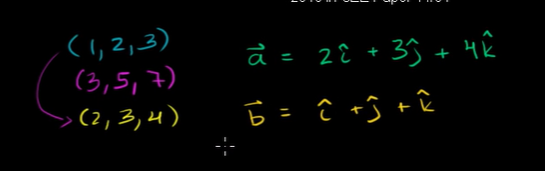
If we cross product two vectors, we can get a normal vector which is perpendicular to the plane!

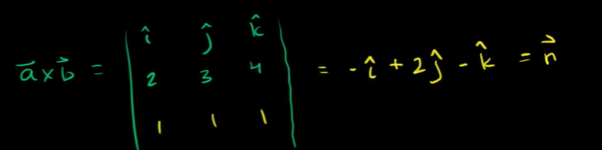
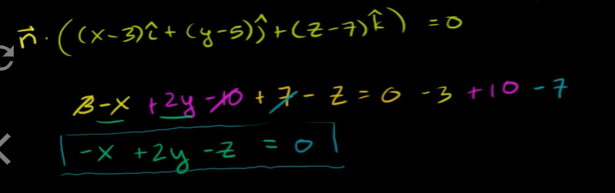
And the blue plane and orange plane are parallel, so they should have the same coefficients on each terms(x,y,z).

So we know that A will be equal to 1.

Now let's figure out the actual distance between these two planes.

Using the distance formula,

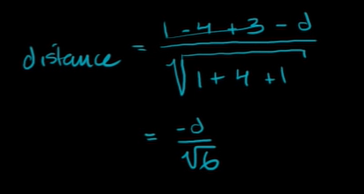
Hence, d will be equal to -6.