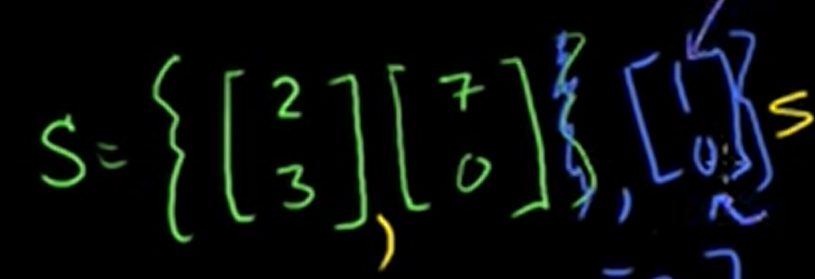Linear subspaces

Subspace of $R \space ^ n$

V is some subsset of vectors, some subset of $R \space ^ n$ .

In order for V to be a subspace or a linear subspace of $R \space ^ n$ , This means three things.

📖 Defintion of subspace
1. V contains $\vec {0}$
2. $\vec {x}$ in V $\longrightarrow$ $c \cdot \vec {x}$ in V (Closure under Multiplication)
3. $\vec {a}, \vec {b}$ in V $\longrightarrow$ $\vec {a} + \vec {b}$ in V (Closure under addition)

Let's see an example.

S = {$\left[ \begin{matrix} x_1 \\ x_2 \end{matrix}\right] \space \in R^2 | x_1 \ge 0$}

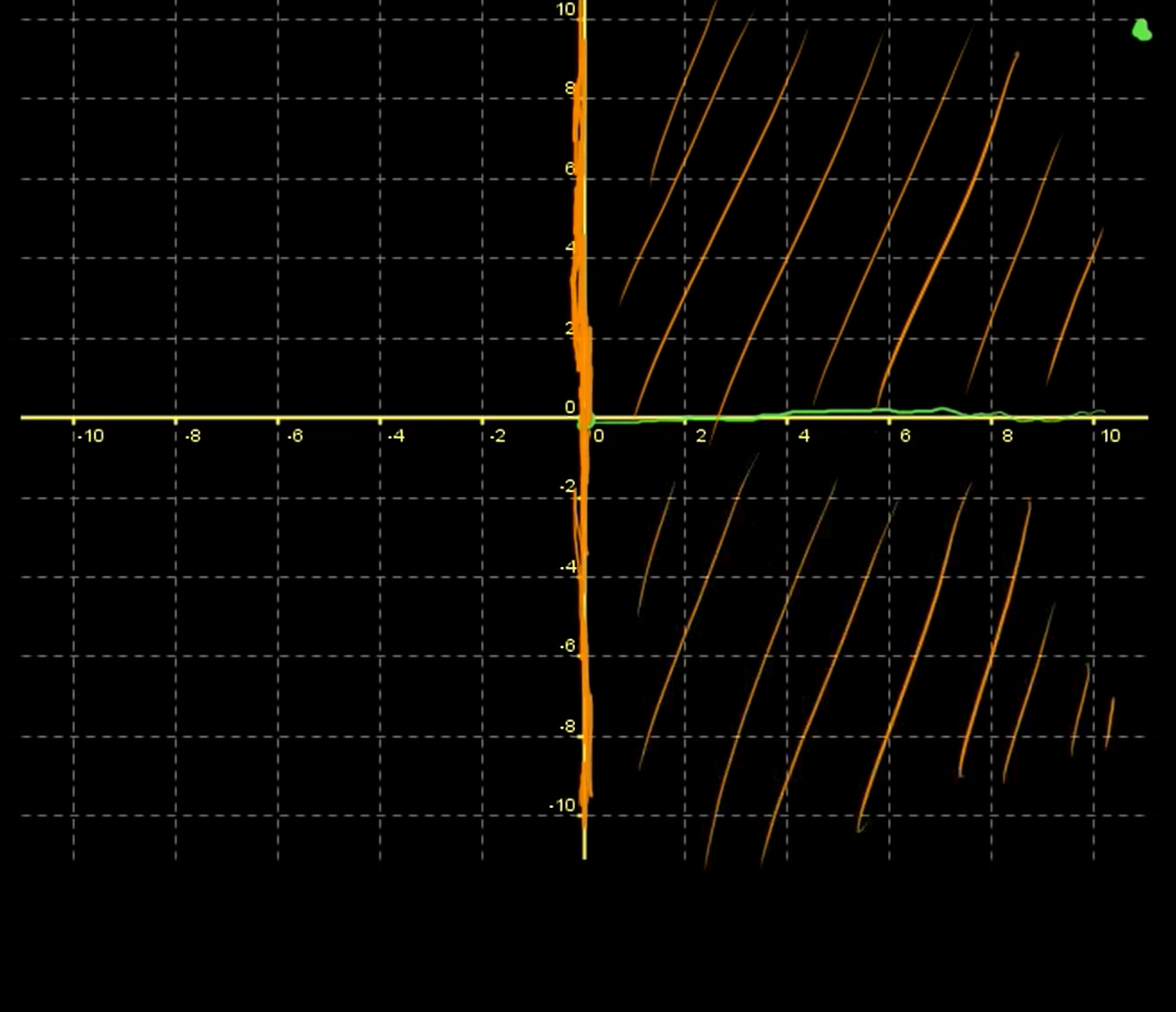
The question is that is S a subspace of $R^2$?

1. Does contain zero vector? Yes!
2. Closed under scalar multiplication? No!
3. Closed under addition? Yes!

$\therefore$ This is not a subspace of $R^2$!

Basis of a subspace

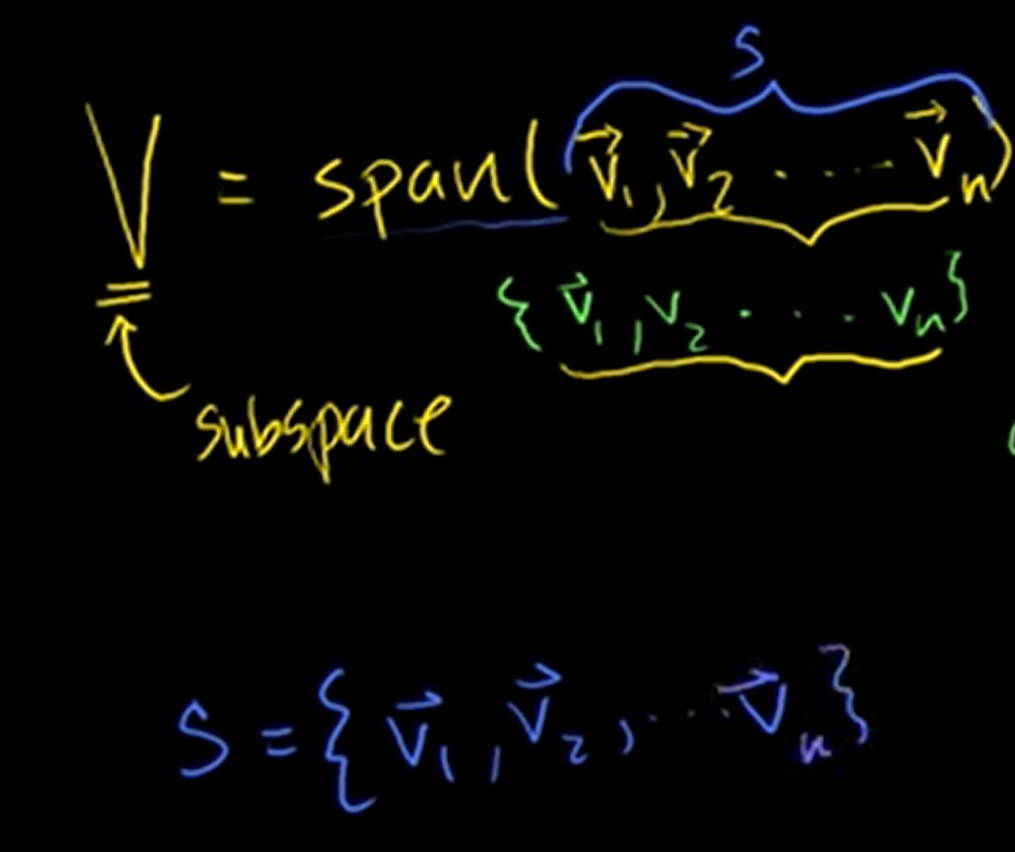
Let's say we have set V, S.

S is a basis for V.

If something is a basis for a set, that means that those vectors, you can get to any of the vectors in that subspace and that those vectors are linearly independent.

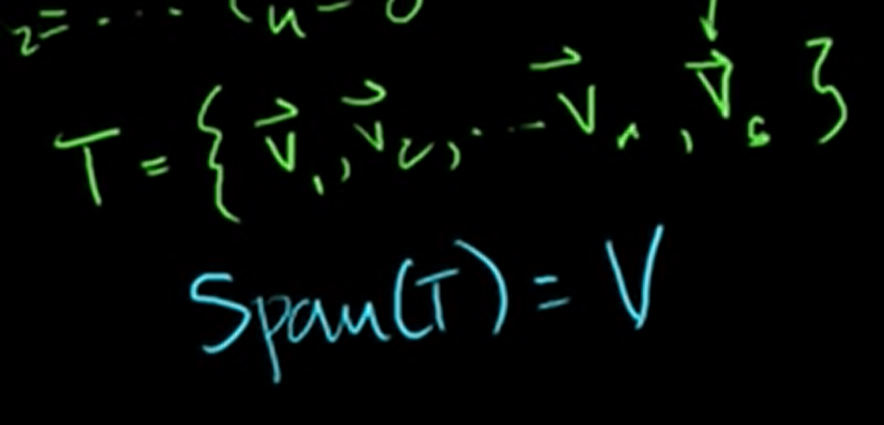
Let's see another set T. still, span of T is V. This set is linearly dependent because of $\vec {v_s}$.

Basis is the minimum set of vector that spans the subspace.

And these are standard basis of $R^2$. What's useful about a basis is that you can represent any vector in your subspace by some unique combination of the vectors in your basis.

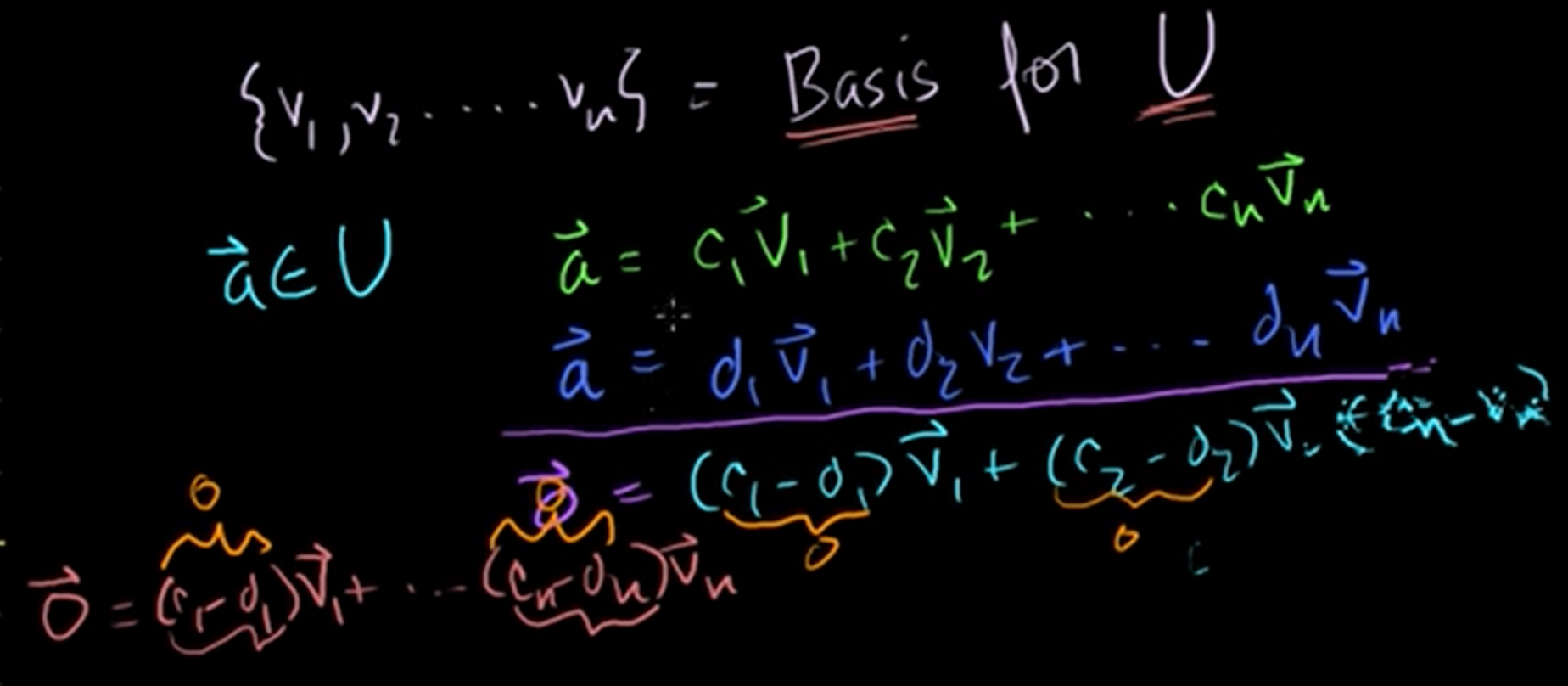
By the fact that it's linearly independent, each of these constants have to be equal to each other. So if you have a basis for some subspace, any memeber of that subspace can be uniquely determined by a unique combination of those vectors.

❓ Is this set a basis for $R^2$?

❗ No! It clearly will continue to span $R^2$ but these two guys alone span $R^2$.
So therefore, this is not a linearly independent set.