해밍 코드 (Hamming Code)

해밍 코드란?

데이터 전송 시 1비트의 에러를 정정할 수 있는 자기 오류정정 코드를 말한다. 패리티비트를 보고, 1비트에 대한 오류를 정정할 곳을 찾아 수정할 수 있다. (패리티 비트는 오류를 검출하기만 할 뿐 수정하지는 않기 때문에 해밍 코드를 활용)

수학자 리처드 웨슬리 해밍(Richard Wesley Hamming)이 1940년대 말에 벨(Bell) 연구소에서 개발하여 1950년에 작성된 저서에 소개 되어있는데, 그의 이름을 따서 해밍 코드(Hamming Code)라고 명명되었다.

해밍 코드는 데이터 비트에 몇가지의 패리티 비트가 추가된 코드이다. 기존의 패리티 비트들은 수신된 데이터열에 에러 유무만 확인할 수 있었는데, 해밍 코드를 이용하면 에러 비트의 위치뿐만아니라 정정도 가능하다.

추가되는 패리티 비트 수 구하기

위 공식에 따라 패리티 비트별 사용한 데이터 비트 수의 예시는 다음과 같다.

p = 3 -> d = 2 ~ 4
p = 4 -> d = 5 ~ 11
p = 5 -> d = 12 ~ 26

패리티 비트 위치

예시를 통해 해밍 코드를 만들기 위해 추가되는 패리티 비트의 수와 위치를 알아보자.

먼저 데이터 비트 수가 8인 경우 추가되는 패리티 비트의 수는 위 공식에 따라 다음과 같다.

즉, 위 식을 만족하는 p의 최소값은 4이고, 해밍 코드의 전체 비트 수는 12이다.

그럼 패리티 비트와 데이터 비트의 위치는 다음과 같다.

패리티 비트 체크 범위 확인 및 패리티 비트의 값 결정

각 패리티 비트의 체크 범위는 다음과 같은 규칙을 통해 결정된다.

n 번째 패리티 비트는 n 번째에서 시작하며, n 비트 만틈을 포함하고 n 비트씩 건너뛴 비트들을 대상으로 패리티 비트 범위를 지정하고 각 피리티 비트를 결정한다.

위의 규칙에 따라 결정된 패리티 비트의 체크 범위는 다음과 같다.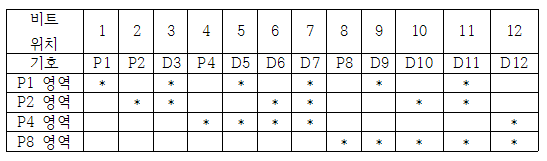

P1의 영역 = D3 + D5 + D7 + D9 + D11
P2의 영역 = D3 + D6 + D7 + D10 + D11
P4의 영역 = D5 + D6 + D7 + D12
P8의 영역 = D9 + D10 + D11 + D12

이를 이용해 패리티 비트의 값을 결정할 수 있다.
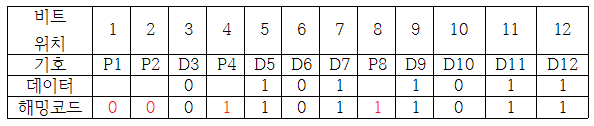
만약 전송할 데이터 비트가 01011011(91)이고 짝수 패리티 비트를 사용한다면 생성된 해밍 코드는 다음과 같다.

P1 = D3 + D5 + D7 + D9 + D11 = 0 + 1 + 1 + 1 + 1 = 0
P2 = D3 + D6 + D7 + D10 + D11 = 0 + 0 + 1 + 0 + 1 = 0
P4 = D5 + D6 + D7 + D12 = 1 + 0 + 1 + 1 = 1
P8 = D9 + D10 + D11 + D12 = 1 + 0 + 1 + 1 = 1

오류 검출 및 오류 비트 수정

해밍 코드를 통해 오류 검출 및 오류 비트를 수정하려면 신드롬(Syndrome) 값을 구하고 이를 통해 이루어진다.

신드롬(Syndrome)

패리티 비트를 포함하여 얻은 2진수 값으로 0 ~ 15 사이의 값으로 만들어지는 오류 값이다.
만약 신드롬 값이 0이라면 오류가 없은 것이며, 만약 신드롬 값이 6이면, 6번째 비트인 D6에서 오류가 발생한 것이다.

신드롬 값 구하기

신드롬 값은 위에서 언급했듯 패리티 비트를 포함하여 검사하며, 짝수 패리티 비트이기 때문에 신드롬 또한 짝수 규칙을 따라 계산한다.

C1 = P1 + D3 + D5 + D7 + D9 + D11 = 0+ 0 + 1 + 1 + 1 + 1 = 0
C2 = P2 + D3 + D6 + D7 + D10 + D11 = 0 + 0 + 0 + 1 + 0 + 1 = 0
C4 = P4 + D5 + D6 + D7 + D12 = 1 + 1 + 0 + 1 + 1 = 0
C8 = P8 + D9 + D10 + D11 + D12 = 1 + 1 + 0 + 1 + 1 = 0

이렇게 계산된 신드롬을 2진수 값으로 바꾼다.

0bC1C2C4C8 = 0b0000 = 0

계산된 신드롬 값이 0 이므로 위 예제에서는 오류가 없다.

오류가 있는 경우

C1 = P1 + D3 + D5 + D7 + D9 + D11 = 0+ 0 + 1 + 1 + 1 + 0 = 1
C2 = P2 + D3 + D6 + D7 + D10 + D11 = 0 + 0 + 0 + 1 + 0 + 0 = 1
C4 = P4 + D5 + D6 + D7 + D12 = 1 + 1 + 0 + 1 + 1 = 0
C8 = P8 + D9 + D10 + D11 + D12 = 1 + 1 + 0 + 0 + 1 = 1

계산된 신드롬을 2진수 값으로 바꾸면 다음과 같다.

0bC1C2C4C8 = 0b1101 = 11

신드롬 값은 11로 즉, D11에 위치한 비트가 오류가 발생했다는 것을 알 수 있다.
0을 반전하여 데이터를 정정해 000110111011로 수정한다.

참고 자료
https://github.com/gyoogle/tech-interview-for-developer/blob/master/Computer%20Science/Computer%20Architecture/%ED%8C%A8%EB%A6%AC%ED%8B%B0%20%EB%B9%84%ED%8A%B8%20%26%20%ED%95%B4%EB%B0%8D%20%EC%BD%94%EB%93%9C.md
https://joy023.tistory.com/139
https://dreamlog.tistory.com/578
https://ko.wikipedia.org/wiki/%ED%95%B4%EB%B0%8D_%EB%B6%80%ED%98%B8
https://m.blog.naver.com/ggggamang/221113176831
http://www.ktword.co.kr/test/view/view.php?m_temp1=1212
http://www.ktword.co.kr/test/view/view.php?m_temp1=5779&id=964
https://unfunhy.tistory.com/116