1. Binary Search Tree를 왜 사용하는가
-
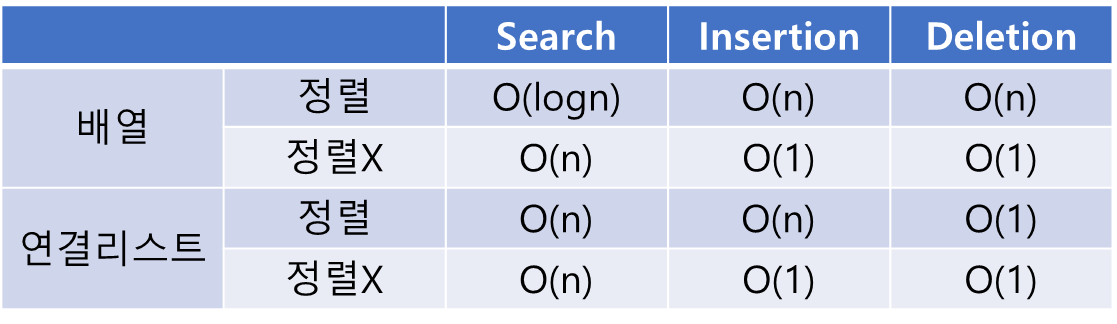
정렬이 된 배열은 Inertion와 Deletion를 한 후 Shift 과정에서 O(n)이 된다.
-
정렬이 되지 않은 배열은 Insertion에서 Memory Reallocation을 포함하면 O(n)이 된다.
-
정렬이 되지 않은 연결 리스트의 Insertion은 리스트의 맨 앞에 노드를 추가한다.
-
위 표에서 정렬되지 않은 배열과 정렬되지 않은 연결 리스트의 Deletion은 Target Node를 Seach하는 시간은 포함하지 않는다.
배열과 연결 리스트 자료 구조는 시간복잡도가 O(n)이 되는 연산을 하나 이상 포함하고 있다.
이진 트리 자료 구조를 사용하면 시간 복잡도는 최대 O(h) (h는 Tree의 높이)가 되며, Complete Tree인 경우에 O(logn)이 된다.
2. Heap과 BST의 차이점
- Heap은 Complete Binary Tree여야 한다.
- BST는 제약 조건이 없다.
- 높이가 n인 트리를 Skewed Tree라고 한다.
3. BST의 연산
1) Insertion
- Pseudo Code

- 추가할 노드의 부모 노드부터 정한다.
- 부모 노드의 왼쪽 혹은 오른쪽 자식을 결정한다.
2) Search
- Pseudo Code

3) Minimum Value
- Pseudo Code

최솟값은 항상 가장 왼쪽 노드에 존재한다.
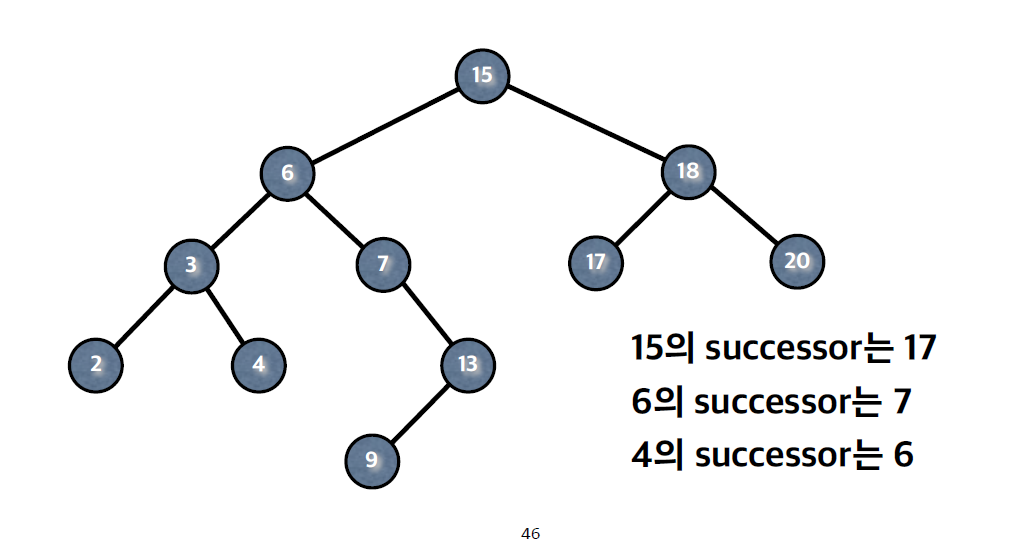
4) Successor
: 트리에서 해당 노드와 가장 가까운 값
: 보통 해당 노드보다 큰 값중에서 가장 작은 값을 Successor로 선택한다.
- Pseudo Code

노드 x의 Successor을 찾는 3가지 경우
1. x의 오른쪽 부트리가 존재할 경우, 오른쪽 부트리의 최솟값
2. x의 오른쪽 부트리가 존재하지 않는 경우, 부모의 오른쪽 Edge를 올라가다 (x보다 작은 노드들) 처음으로 부모의 왼쪽 Edge로 올라가서 만난 노드 (x보다 큰 노드 중 가장 작은 노드)
3. x가 최댓값인 경우 Successor가 존재하지 않는다.
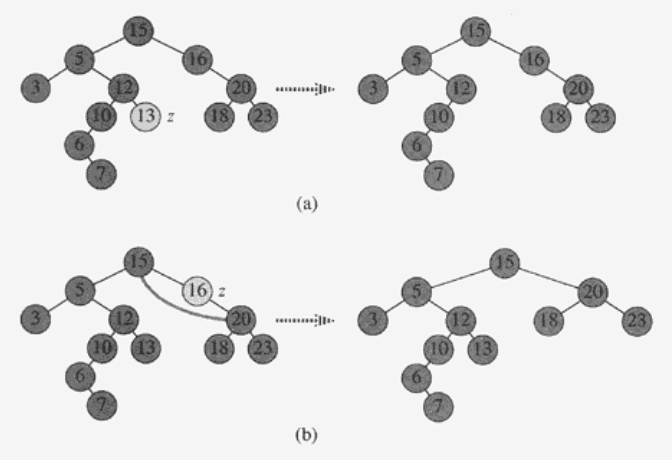
5) Deletion
- Pseudo Code

- y는 Delete할 노드이다.
- 자식 노드가 0개 또는 1개인 경우 y는 z (target node)가 된다.
- 자식 노드를 parent에 연결한다.
- y를 delete한다.
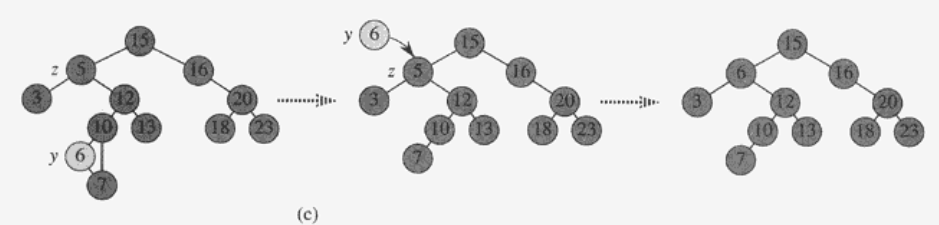
- 그렇지 않으면 y는 z의 successor가 된다.
- y를 z의 parent노드와 연결한다.
- z에 y의 값을 복사한다.
- y를 delete한다.
6. Traversal
- Inorder
: Left-subtree -> root -> right-subtree

-
Preorder
: Root -> left-subtree -> right-subtree -
Postorder
: Left-subtree -> right-subtree -> root
Left-subtree가 Right-subtree보다 우선순위가 높다.
- Level-order
: Traverse in depth using a queue