Non-Comparison Sort

1. Comparision Sort

• 데이터 간의 상대적인 크기 관계만을 이용한다.

• Bubble Sort, Quick Sort...

어떤 Comparison Sort도 시간 복잡도가 O(nlogn)보다 낮을 수 없다.

• 모든 Comparison Sort는 Decision Tree 나타낼 수 있다.

• 다음은 크기가 3인 배열의 삽입 정렬 알고리즘의 Decision Tree이다.

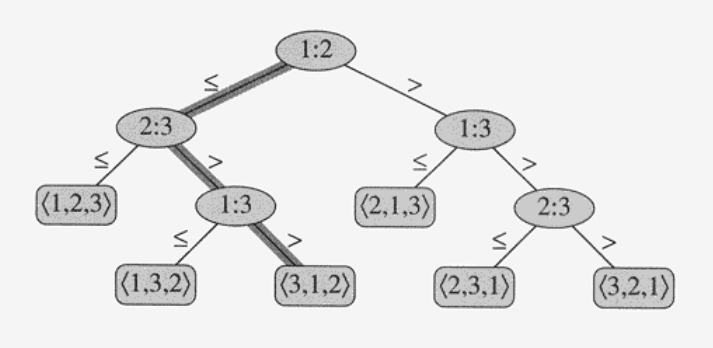
알고리즘의 정렬 과정은 특정 Depth가 된다.

• 첫 번째 값이 두 번째 값보다 작고, 두 번째 값이 세 번째 값보다 적으면 <1,2,3>으로 Sorting한다.

따라서 Comparison Sort의 시간복잡도는 최악의 경우 Decision Tree의 높이와 비례한다.

• Decision Tree는 정렬을 마치면 총 n!개 (배열의 Permutation)의 leaves를 갖는다.

• Tree의 높이가 가장 낮은 경우는 Complete Tree인 경우로, log(n!)이다.

따라서 height >= logn! = θ(nlogn)이므로 Comparison Sort는 시간복잡도가 θ(nlogn)보다 작을 수 없다.

2. Non-Comparison Sort

• 데이터에 대한 사전 지식을 이용한다.

• Bucket Sort, Radix Sort...

3. Counting Sort

특징

• 원소들 중 가장 큰 값 (k) 크기의 배열을 생성하여 정렬에 이용한다.

• Stable Sort이다.
  : 동일한 데이터가 존재한다면 처음으로 입력된 값이 처음으로 출력된다. (레이블 정렬에 필수적이다.)

• θ(n + k)의 시간 복잡도를 가진다.
  : k는 원소 중 가장 큰 값을 의미한다.
  : k가 클 경우 비실용적이다.

n >> k 인 경우 사용하면 시간복잡도는 θ(n)이다.

알고리즘

1. Count 배열을 만들어 index 순서대로 각 원소들의 빈도를 저장한다.

2. Count 배열의 0 index부터 누적합을 저장한다.

3. 기존 배열의 끝 부터 결과 배열로 해당하는 Count 배열의 index로 옮긴다.

코드

#pragma once
#include <stdlib.h>
#include <stdio.h>

void countSort(int* data, int length, int max_value) {
	int* result = (int*)malloc(sizeof(int) * length);
	int* count = (int*)malloc(sizeof(int) * (max_value + 1));

	for (int i = 0; i <= max_value; i++) {
		count[i] = 0;
	}
	
    // 1
	for (int i = 0; i < length; i++) {
		count[data[i]]++;
	}

	// 2
	for (int i = 1; i <= max_value; i++) {
		count[i] += count[i - 1];
	}

	// 3
	for (int i = length - 1; i >= 0; i--) {
		result[count[data[i]] - 1] = data[i];
		count[data[i]]--;
	}

	for (int i = 0; i < length; i++) {
		data[i] = result[i];
	}
}

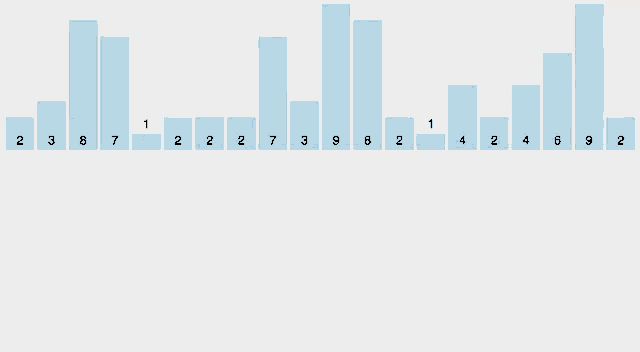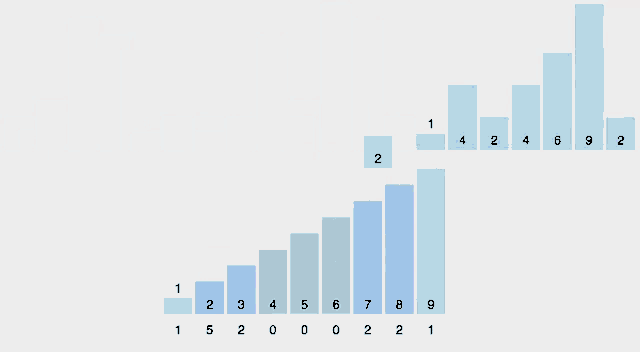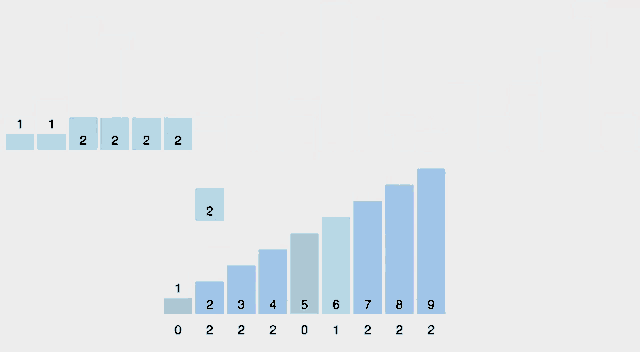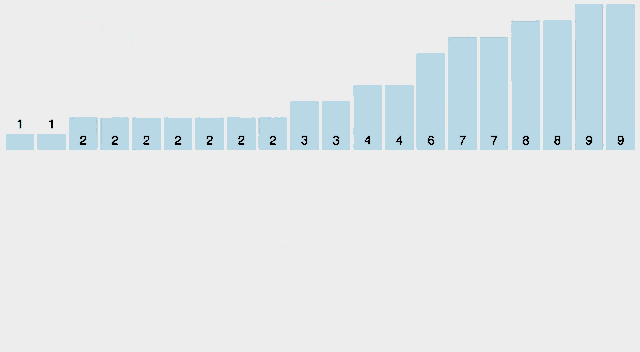
4. Radix Sort

특징

• 원소 중 가장 큰 정수의 자릿수 d를 알아야 한다.

• Counting Sort를 이용하면 한 자릿수당 시간 복잡도는 θ(n+k)이다.

d개의 자릿수가 있으므로 시간 복잡도는 θ(d(n+k))이고, d와 k가 상수일때 θ(n)이다.

알고리즘

• 1의 자릿수 부터 Stable Sort를 실행하여 전체 배열을 정렬한다.

코드

#pragma once
#include <stdio.h>
#include <limits.h>
#include <stdlib.h>

void radixSort(int* data, int length, int digit) {
	int exp = 1;
	for (int i = 1; i <= digit; i++) {
		// for every digit number
		// do stable sort
		int max_value = INT_MIN;

		int* digits = (int*)malloc(sizeof(int) * length);

		// get the greatest digit
		for (int j = 0; j < length; j++) {
			digits[j] = (data[j] % (exp * 10)) / exp;

			if (digits[j] > max_value) {
				max_value = digits[j];
			}
		}

		int* count = (int*)malloc(sizeof(int) * max_value);
		int* result = (int*)malloc(sizeof(int) * length);
		
		for (int j = 0; j <= max_value; j++)
			count[j] = 0;

		for (int j = 0; j < length; j++) {
			count[digits[j]]++;
		}

		for (int j = 1; j <= max_value; j++) {
			count[j] += count[j - 1];
		}

		for (int j = length - 1; j >= 0; j--) {
			result[count[digits[j]] - 1] = data[j];
			count[digits[j]]--;
		}

		for (int j = 0; j < length; j++)
			data[j] = result[j];

		printf("%d's digit:\n", exp);
		for (int j = 0; j < length; j++) {
			printf("%d ", data[j]);
		}
		printf("\n");
		exp *= 10;
	}
}